Задачи, сгруппированные по методам решения. Метод вложенных матриц

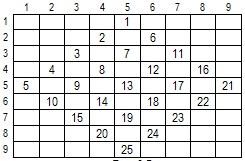
Задача 4: Заполните матрицу, как показано на рис.9.5:

Рис. 9.5.

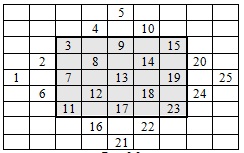
Дополнительные сведения: Есть в информатике классическая задача "Магический квадрат" (в "Магическом квадрате" сумма элементов всех строк, всех столбцов и всех диагоналей равна). Решать ее можно различными способами, один из которых называется методом "Террас". Для создания Магического квадрата размерностью n x n (n - нечетное число) необходимо заполнить двумерный массив размерностью (2n-1)x(2n-1) так, как в на рис.9.6:

Рис. 9.6.

Затем "треугольники", выступающие за пределы жирной рамки перенести внутрь таким образом (табл.9.3):

В полученном двумерном массиве сумма элементов всех строк и всех столбцов равна.

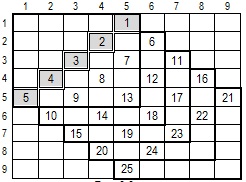
Идея решения: Разбиваем исходную матрицу на "вложенные". В каждой матрице заполняем побочную диагональ:

Рис. 9.7.

Решение очевидно.

Ключевые термины

• Магический квадрат - двумерный массив, сумма элементов каждой строки, каждого столбца и каждой диагонали которого одинакова.
• Метод "Террас" - способ создания магического квадрата
• Решето Эратосфена - алгоритм нахождения простых чисел.
• Скатерть Улама - узор из простых чисел, расположенных по спирали.

Краткие итоги

При заполнении некоторых двумерных массивов проглядывается некоторая закономерность (способ заполнения повторяется). Мысленно "разберем" двумерный массив на "вложенные" - как бы независимые друг от друга массивы, для заполнения которых используется один и тот же способ. Разрабатываем для каждого из них алгоритм заполнения, затем находим зависимость, объединяющую все алгоритмы в один.

Данный способ поможет решить такие задачи, как создание Магического квадрата методом "Террас", создание "Скатерти Улама" при помощи "Решета Эратосфена".

Набор для практики

Вопросы.

• Каким образом можно заполнить двумерный массив числами натурального ряда чисел?
• Каков порядок обхода элементов двумерного массива, если счетчик внешнего цикла используется в качестве первого индекса элемента массива, счетчик внутреннего цикла - в качестве второго индекса?
• Каков порядок обхода элементов двумерного массива, если счетчик внешнего цикла используется в качестве второго индекса элемента массива, счетчик внутреннего цикла - в качестве первого индекса?

Упражнения.

• Заполните массив по образцу (табл.9.4):

  Таблица 9.4.

  1	2	3	4	5	6	7
  14	13	12	11	10	9	8
  15	16	17	18	19	20	21
  28	27	26	25	24	23	22
  и т.д.	...	...	...	...	...	...
  ...	...

• Заполните массив по образцу (табл.9.5):

  Таблица 9.5.

  1	2	6	7	15	16	28
  3	5	8	14	17	27
  4	9	13	18	26
  10	12	19	25
  11	20	24
  21	23
  22

• Заполните массив по образцу (табл. 9.6):

  Таблица 9.6.

  22	16	11	7	4	2	1
  	23	17	12	8	5	3
  		24	18	13	9	6
  			25	19	14	10
  				26	20	15
  					27	21
  						28