| Россия, г. Москва |
Комбинаторика. Формирование комбинаторных групп из N по К (К - от 1 до N)
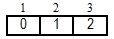
Пусть N=4. Необходимо сформировать различные группы элементов выбираемых из исходного множества. Количество элементов в выборке от 1 до N. Элементы исходного множества будем хранить в массиве А (рис. 12.1):
Составим таблицу, в которой выбранный элемент отметим "1", невыбранный - "0":
Итого, сформированы группы: {3}, {2}, {2, 3}, {1}, {1,3}, {1, 2}, {1, 2, 3}.
Для формирования групп потребовалось перебрать все варианты комбинаций "0" и "1". Такой метод формирования комбинаторных групп называется "Двоичным перебором", а количество групп будет равно 2n-1.
Идея решения: для выбора элементов из исходного множества необходимо получить двоичный код (на единицу больше предыдущего). Первый вариант получения нового двоичного кода - перевод счетчика цикла i из десятичной в двоичную систему счисления. Второй вариант получения очередного двоичного кода - ищем в массиве двоичных кодов d последний нулевой элемент , заменяем его на единицу и обнуляем все следующие за ним элементы (этот метод называется лексикогрофическим порядком).
Количество возможных комбинаций двоичных кодов 2^n-1 (исключаем двоичный код, состоящий из одних нулей).
Программная реализация на Бейсике:
input "введите количество элементов исх. множества="; n
for i=1 to n
input "введите элемент"; a(i)
next
for i=1 to 2^n-1
rem=поиск первого нулевого элемента=========
for j=1 to n
if d(j)=0 then x=j
next
rem=формирование двоичного кода===========
for z=x to n
d(z)=0
next z
d(x)=1
rem=печать элементов====================
for j=1 to n
if d(j) <> 0 then print a(j);
next j
print
next iПрограммная реализация на Паскале:
const nn=10;
var a,d: array [1..nn] of integer;
i,n,x,j,z,st: integer;
begin
writeln ('количество элементов');
readln (n);
for i:= 1 to n do
begin
writeln ('введите элемент');
readln (a[i]);
end;
{=формирование двоичного кода===}
st:=1;
for i:=1 to n do
st:=st*2;
for i:= 1 to (st-1) do
begin
for j:= 1 to n do
if d[j]= 0 then x:= j;
for z:= x to n do
d[z]:=0;
d[x]:=1;
{=печать элементов========}
for j:= 1 to n do
if d[j]<>0 then write (a[j]);
writeln;
end;
end.Тест:
Если предположить, что каждый элемент из исходного набора может повторяться во вновь созданной комбинаторной группе от 0 до n раз, то необходимо организовать n-ричный перебор.
Задачи:
- "Размен монет": дана купюра достоинством X. Требуется разменять ее монетами по 1, 5, 10, 50 рублей.
- Даны гири массами M1, M2, M3, M4. Как можно взвесить предмет массой X?
- Даны N чисел. Выделите из них группы, содержащие от 1 до N элементов, каждая из которых имеет сумму X.
Программная реализация на Бейсике:
input "x="; x
input "количество элементов в исходном множестве"; n
for i = 1 to n
input "введите элемент"; a(i)
next
for i = 1 to (2^n - 1)
rem==получение следующего двоичного кода==
for j = 1 to n
if d(j) = 0 then k = j
next j
for z = k to n
d(z) = 0
next z
d(k) = 1
rem=============================
s = 0
for j = 1 to n
if d(j) <> 0 then s = s + a(j)
next j
rem========вывод результата==========
if s = x then
for ii = 1 to n
if d(ii) <> 0 then print " "; a(ii);
next ii
end if
print
next iПрограммная реализация на Паскале:
const nn=10;
var a,d: array [1..nn] of integer;
ii,i,n,x,j,z,st,k: integer;
begin
writeln ('введите с чем сравнивать);
readln (х);
writeln ('введите количество элементов');
readln (n);
for i:= 1 to n do
begin
writeln ('введите элемент');
readln (a[i]);
end;
{=вычисление количества возможных комбинаций=}
st:=1;
for i:=1 to n do
st:=st*2;
{=================================}
for i:= 1 to (st-1) do
begin
{=получение следующего двоичного кода===}
for j:= 1 to n do
if d[j]= 0 then k:= j;
for z:= k to n do
d[z]:=0;
d[k]:=1;
{=============================}
s: = 0;
for j: = 1 to n do
if d[j] <> 0 then s:= s + a[j];
if s = x then
{=====вывод результата=========}
for ii:= 1 to n do
if d[ii] <> 0 then write (a[ii]);
writeln;
end;
end.Тест:
Ключевые термины
- Двоичный перебор - метод формирования комбинаторных групп из исходного множества элементов, на которые "указывают" единицы в соответствующем разряде двоичного кода.
- Лексикографический порядок - метод получения очередного двоичного кода.
Краткие итоги
Создание комбинаторных групп двоичным перебором основывается на использовании натурального ряда двоичных чисел.
Двоичный код (поразрядно) хранится в дополнительном массиве, имеющем такую же размерность, что и массив с исходным множеством элементов. В массиве двоичных кодов на каждом шаге получаем новый двоичный код, единицы которого "указывают" на соответствующие разряды массива исходного множества.
Получение очередного двоичного кода в лексиграфическом порядке предполагает такой алгоритм: массив с двоичным кодом обходится справа налево, ищется первый ноль, он заменяется на единицу, а все элементы, стоящие левее - обнуляются.
Набор для практики
Вопросы.
- В чем заключается метод двоичного перебора при формировании комбинаторных групп?
- Укажите количество разнообразных n-разрядных двоичных кодов.
- Каким образом можно получить следующее за текущим двоичное число (алгоритм получения)?
- Что изменится в алгоритме формирования комбинаторных групп, если состояние исходных объектов можно охарактеризовать не только как "выбран"/"не выбран": выбранный объект также градируется ("выбран в соответствии с условием 1"/" выбран в соответствии с условием 2")?
Упражнения.
- Ввести с клавиатуры целое число n. Вывести натуральный ряд двоичных чисел до числа, десятичное представление которого не превосходит n.
- Тур-фирма предлагает разнообразные путевки, хранящиеся в базе данных в виде названий туров и их стоимостей (всего n туров). Сделать выборку из базы данных тех туров, которые подходят покупателю по цене (покупатель рассчитывает приобрести не более трех путевок не менее, чем на m рублей).