Задачи

1. Выписать решение задачи Коши для уравнения роста численности популяции при отсутствии лимитирующих факторов. Решить конкретную задачу при k=0,01. Указание: прирост пропорционален численности или \[ x'(t)=k\pi x(t) \] .
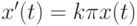2. Выписать решение задачи Коши для уравнения развития отрасли при f(t)=0,1t²+0,2t+1, x(t₀)=1. Указание: темп производства пропорционален объему (в идеальных условиях не лимитируемого производства) производимой продукции или 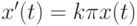\[ x'(t)=k\pi x(t) \] , где, например, k – коэффициент вложений в производство, x(t₀)=1 – задано.
3. Выписать решение задачи о распространении технологии при k=0,02 и максимальном уровне насыщения технологией х_max=100. Указание: x’(t)=k[x_max-x(t)], x(0)=x₀ .

4. Решить задачу Коши:

   • x’(t)=5x²t, x(0)=1 ;
   • xy’(x)=(x+1)(y–1), y(1)=2 ;
   • y’(x)–хy=3, y(0)=1.

   Указание: а), б) – разделить переменные; в) решить сперва однородное уравнение, разделив переменные.

5. Решить уравнение:

   • y’’(x)+y=0 ;
   • y’’(x)–y’+y=0 ;
   • y’’(x)+y’–2y=0.

   Указание: выписать характеристическое уравнение и найти его корни.

6. Найти решение задачи:

   \[ y’’(x)+y’=0, y’(0)=1, y(0)=2. \]

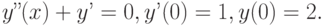
   Указание: выписать характеристическое уравнение и найти его корни.

7. Исследовать на сходимость ( расходимость ) ряд:

   • \[ \cfrac12+\cfrac15+\cfrac 18 + \dots + \cfrac {1}{3n-1}+ \dots =\sum\limits_{n=1}^{\infty}\cfrac {1}{3n-1} \] ;
   • \[ 1+ \cfrac{1}{2^2}+\cfrac{1}{3^2} + \dots + \cfrac{1}{n^2}+\dots=\sum\limits_{n=1}^{\infty}\cfrac {1}{n^2} \] ;
   • \[ \cfrac{1}{\ln2}+\cfrac{1}{\ln3}+\cfrac{1}{\ln4}+\dots+\cfrac{1}{\ln n}+\dots=\sum\limits_{n=2}^{\infty}\cfrac {1}{\ln n} \] ;
   • \[ \cfrac12-\cfrac15+\cfrac 18 - \dots + (-1)^{n+1}\cfrac {1}{3n-1}+\dots=\sum\limits_{n=1}^{\infty}\cfrac {(-1)^{n+1}}{3n-1} \] .

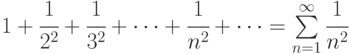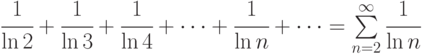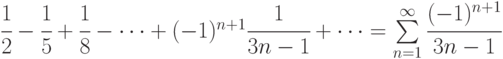   Указание: использовать метод сравнения, например, с гармоническим рядом а); геометрической прогрессией б).

8. Найти интервал сходимости степенного ряда:

   \[ x+\cfrac{x^2}{2}+\cfrac{x^3}{3}+\dots+\cfrac{x^n}{n}+\dots=\sum\limits_{n=1}^{\infty}\cfrac {x^n}{n}. \]

   Указание: использовать формулу для радиуса сходимости степенного ряда.

9. Найти интервал сходимости ряда:

   \[ x^2+\cfrac{x^4}{2}+\cfrac{x^6}{3}+\dots+\cfrac{x^{2n}}{n}+\dots=\sum\limits_{n=1}^{\infty}\cfrac {x^{2n}}{n}. \]

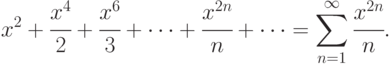
   Указание: использовать формулу для радиуса сходимости степенного ряда.

10. Разложить в ряд Маклорена функцию:

    • y=cos(x) ;
    • y=e^x ;
    • y=e^x+2 .

11. Указание: выписать через производные коэффициенты ряда.

Темы научных исследований и рефератов (Интернет-листов)

1. Теоремы о непрерывности, их приложения.
2. Теоремы о дифференцируемости, их приложения.
3. Теоремы об интегрируемости, их приложения.
4. Дифференциальные уравнения, разнообразие и единство мира.
5. Задача Коши, его история и эволюция.
6. Основные (базовые) методы решения обыкновенных дифференциальных уравнений.
7. Ряды конечные и бесконечные, их философский анализ и сопоставление. Переход конечного в бесконечное.
8. Функциональные ряды.
9. Приложения рядов.
10. Роль непрерывного анализа в развитии математической и общей культуры общества.