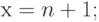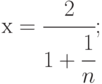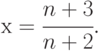НОУ ИНТУИТ | Введение в математику. Практикум. Лекция 2: Величины и их значения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.01.2008 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать программу

Аннотация: Решение задач, связанных с используемым в математике базовым символическим аппаратом – переменными и постоянными, обучение реферированию и Интернет–поиску по этой теме

Ключевые слова: число, натуральное число, целое число, рациональное число, иррациональное число, вещественное число, комплексное число, монотонная величина, ограниченная величина, промежуток, окрестность, относительная погрешность, погрешность, действительное число

Задачи

Указать, какие числа являются натуральными, целыми, рациональными, иррациональными, вещественными, комплексными:

2 ; 34,67 ; -34,0 ; 0,0 ; 0 ; 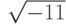$\sqrt{46}$ ; $–8\sqrt{\cfrac{46}{61}}$ ; $\sqrt{-11}$ ; 0,01 ; –0,009.

Обосновать ответ. Указание: множество комплексных чисел включает множество вещественных, множество вещественных включает в себя множества рациональных и иррациональных, которые не пересекаются, множество рациональных включает в себя множество целых, которое включает в себя множество натуральных чисел.
Указать монотонные и ограниченные переменные х (n=1,2,...):
- $х=\cfrac{2}{1+\cfrac{1}{n}};$
- $х=\cfrac{n+3}{n+2}.$
Обосновать ответ (докажите монотонность и ограниченность, если это выполнено). Указание: найти a, b: a<x, x<b, проверить соотношения x(n) и x(n+1) при всех n.
Указать промежутки, образующие – окрестность числа а, определив при этом центр и радиус:

(—1,55; 2,03), (5; 6), (1,111; 9,002).

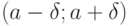Запишите окрестности этих же точек с радиусом, меньшим в 10 раз. Указание: должно быть выполнено условие $(a - \delta ; a + \delta )$ .
При измерении 1 кг товара на одних весах получено приближенное значение 996 гр., а при измерении 200 гр. на других, – 198 гр. Какие весы точнее и почему? Обосновать ответ. Указание: оценить относительную погрешность.
Какое из равенств более точное и почему: 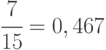$\sqrt{44}=6,63$ ,, $\cfrac{7}{15}=0,467$ ? Обосновать ответ. Указание: оценить относительную погрешность (можно вначале возвести первое выражение в квадрат).
Найти сумму, разность, произведение, частное для двух приближенных чисел а и b и оценить их погрешности: 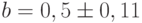$а=0,26 \pm 0,03$ , $b=0,5 \pm 0,11$ . Указание: например, для a + b = 0,76 + 0,14 = 0,90.
Найти максимально возможный и минимально возможный объемы ящика в форме куба со стороной, равной $2,06 \pm 0,03$ . Указание: $V = (2.06 \pm 0.3)^{3}$ .
Составить план измерений, указать минимальный набор инструментов и технологию измерения для решения задачи нахождения среднего арифметического площадей металлических кругов с заданными радиусами от 1 см. до 10 м. Указать нижнюю и верхнюю границы точности вычисления окончательного результата. Указать причины, из–за которых полученный при вычислении результат не совпадает с реальным значением искомого среднеарифметического значения. 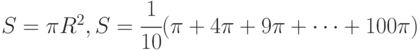Указание: $S = \pi R^2, S = \cfrac{1}{10}(\pi + 4\pi +9\pi +\dots +100\pi)$ .
Доказать, что число 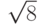$\sqrt{8}$ есть иррациональное число. Указание: можно идти от противного и получить противоречие.
Доказать, что нет рационального числа, квадрат которого равен 5. Указание: можно идти от противного и получить противоречие.