Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.10.2007 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 45 студентам

| Поделиться |

Поддержать программу

Лекция 10:

Подпространства линейного пространства. Евклидово пространство. Линейные преобразования в линейном пространстве. Представление линейного преобразования матрицей. Действия над линейными преобразованиями. Примеры линейных преобразований

A

|

версия для печати

Представление линейного преобразования матрицей

Пусть в n -мерном пространстве R задано преобразование А, которое переводит вектор 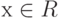$х \in R$ в вектор у m -мерного пространства R₁, т.е. задано преобразование у = Ах. Определим в пространствах R и R₁ базисы соответственно l₁, l₂, ..., l_n и g₁, g₂, ..., g_m. Тогда векторы х и у могут быть представлены в координатной форме следующим образом

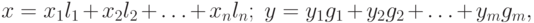$x=x_1 l_1+x_2 l_2+\ldots+x_n l_n;\; y=y_1 g_1+y_2 g_2+\ldots+y_m g_m ,$

( 9.10)

а координаты образа у выражают через координаты прообраза х

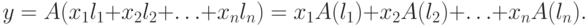$y=A(x_1 l_1+x_2 l_2+\ldots+x_n l_n)=x_1 A(l_1)+x_2 A(l_2)+\ldots+x_n A(l_n).$

( 9.11)

Сравним выражение (9.11) вектора у с выражением (9.10). В результате получим g_i = A(l_i), т.е. образ базиса l₁, l₂, ..., l_n. Разложим А(l₁), А(l₂), ..., А(l_n) по базису g₁, g₂, ..., g_m:

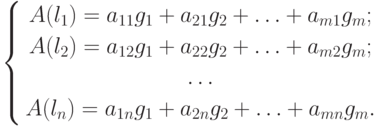$\left\{ \begin{gathered} A(l_1)=a_{11}g_1+a_{21}g_2+\ldots+a_{m1}g_m; \\ A(l_2)=a_{12}g_1+a_{22}g_2+\ldots+a_{m2}g_m; \\ \ldots \\ A(l_n)=a_{1n}g_1+a_{2n}g_2+\ldots+a_{mn}g_m. \end{gathered} \right.$

( 9.12)

Заметим, что выражение (9.12) идентично по своей структуре формулам перехода (9.1).

Подставим выражения (9.12) в формулу (9.11), получим

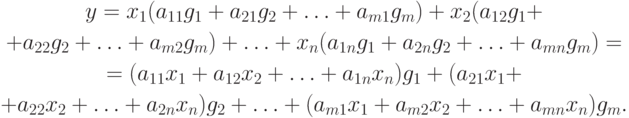
$\begin{gathered} y=x_1(a_{11}g_1+a_{21}g_2+\ldots+a_{m1}g_m)+x_2(a_{12}g_1+ \\ +a_{22}g_2+\ldots+a_{m2}g_m)+\ldots+x_n(a_{1n}g_1+a_{2n}g_2+\ldots+a_{mn}g_m)= \\ =(a_{11}x_1+a_{12}x_2+\ldots+a_{1n}x_n)g_1+(a_{21}x_1+ \\ +a_{22}x_2+\ldots+a_{2n}x_n)g_2+\ldots+(a_{m1}x_1+a_{m2}x_2+\ldots+a_{mn}x_n)g_m. \end{gathered}$

Сравнив последнее выражение с выражением (9.10) для у, можно записать связь между y_j и x_i как

$\left\{ \begin{gathered} y_1=a_{11}x_1+a_{12}x_2+\ldots+a_{1n}x_n; \\ y_2=a_{21}x_1+a_{22}x_2+\ldots+a_{2n}x_n; \\ \ldpts \\ y_m=a_{m1}x_1+a_{m2}x_2+\ldots+a_{mn}x_n. \end{gathered} \right.$

( 9.13)

Если теперь из коэффициентов системы (9.13) составить матрицу

$A= \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix},$

( 9.14)

а из элементов х_i и у_j матрицы-столбцы

$x= \begin{pmatrix} x_1\\x_2\\ \vdots \\ x_n \end{pmatrix} ; \quad y= \begin{pmatrix} y_1\\y_2\\ \vdots \\ y_m \end{pmatrix},$

то систему уравнений (9.13) можно записать в матричном виде y = Ax, именно в таком виде, в каком ранее мы определили линейное преобразование А. Матрица А, определяемая формулами (9.14), называется матрицей линейного преобразования А.

Представим систему (9.12) в матричной записи L = A'(g), где обозначено

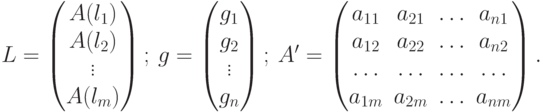$L= \begin{pmatrix} A(l_1)\\A(l_2)\\ \vdots \\A(l_m) \end{pmatrix} ;\ g= \begin{pmatrix} g_1\\g_2\\ \vdots \\g_n \end{pmatrix} ;\ A'= \begin{pmatrix} a_{11} & a_{21} & \ldots & a_{n1} \\ a_{12} & a_{22} & \ldots & a_{n2} \\ \ldots & \ldots & \ldots & \ldots \\ a_{1m} & a_{2m} & \ldots & a_{nm} \\ \end{pmatrix}.$

( 9.15)

Заметим, что матрица A' преобразования является транспонированной матрицей по отношению к матрице А и определяется выражением (9.14).

Определение 27. Если преобразование А переводит какой-либо ненулевой вектор х в нулевой, т.е. А(х) = 0 при $х \ne 0$ , то преобразование А называют вырожденным.

Вырожденное преобразование А задается вырожденной матрицей, у которой detA = 0 (или по теории матриц ранг такой матрицы меньше ее размера).

В дальнейшем будем рассматривать наиболее важный случай, когда матрица преобразования А задается квадратной матрицей, т.е. когда m = n. Тогда говорят, что пространства R и R₁ совпадают или что преобразование А задано в n -мерном пространстве с базисом l₁, l₂, ..., l_n и отображает это пространство в себя.

Таким образом, каждому линейному преобразованию А в заданном базисе l₁, l₂, ..., l_n соответствует квадратная матрица А порядка n и, наоборот, каждая квадратная матрица А порядка n определяет некоторое линейное преобразование А в заданном базисе l₁, l₂, ..., l_n.

Дальше >>

Введение в линейную алгебру

Введение в линейную алгебру

Представление линейного преобразования матрицей

Вопросы и ответы

Студенты

Авторизоваться

Введение в линейную алгебру

Введение в линейную алгебру

Представление линейного преобразования матрицей

Вопросы и ответы

Студенты