|
Добрый день. Подскажите пожалуйста, я прошел ваш курс Введение в линейную алгебру: Информация, - сдал экзамен и у меня высветилось окно, где необходимо оформить доставку сертификата. Однако, я случайно закрыл это окно и теперь не могу найти этот подраздел, чтобы оформить доставку. Где можно это найти? |
Линейные пространства и операции над ними. Определения и аксиомы линейного пространства. Следствия из аксиом линейного пространства
Определения и аксиомы линейного пространства
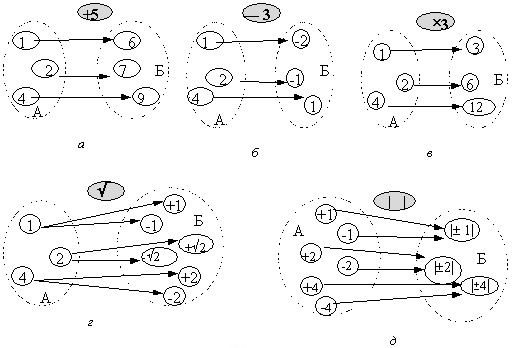
Довольно часто в своей деятельности человеку приходится иметь дело с объектами, связанными между собой некоторыми условными правилами, которые могут быть однозначными (умножение, сложение, вычитание) и многозначными (извлечение корня четной степени из числа, взятие модуля числа). Графически это можно изобразить так, как показано на рис. 7.1.
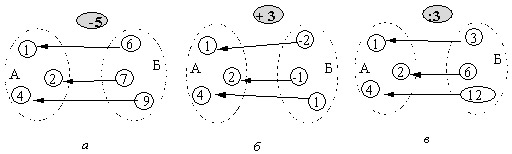
На рис. 7.1а - 7.1в показаны однозначные операции отображения элементов множеств А в элементы множеств Б (прибавление числа 5 к каждому элементу множества А (рис. 7.1а); вычитание числа 3 из каждого элемента множества А (рис. 7.1б); умножение на число 3 (рис. 7.1в) каждого элемента множества А ). Из рисунков видно, что каждому элементу множества А соответствует один и только один элемент множества Б. Очевидно, существует и обратное правило перехода от элементов множества Б к элементам множества А. В указанных случаях это могут быть операция вычитания числа 5 из элементов множества Б (обратная сложению с числом 5), сложение с числом 3 и деление на 3. Схематически обратные операции приведены на рис. 7.2.
Иными словами для прямой операции сложения определена обратная операция вычитание, а для прямой операции умножения - обратная операция деления1Обратная операция деления определена, если число, на которое умножаем, не равно 0 . Заметим, что как для прямой, так и для обратной операции одному элементу множества соответствует один и только один элемент множества Б. Условимся, что если прямая и обратная операции отображения элементов одного множества в элементы другого обладают рассмотренным свойством, то такие операции будем называть взаимнооднозначными.
Иногда одному элементу множества А соответствует два (и более) элемента множества Б (рис. 7.1, г) или двум (или более) элементам множества А соответствует один элемент множества Б (рис. 7.1, д). В этих случаях нельзя заранее сказать, какому именно элементу одного множества будет соответствовать элемент другого множества. Поэтому только указывают количество элементов соответствия. Очевидно, что количество элементов в исходном и отображаемом множествах при таком отображении будет различным.
Попытаемся теперь выполнить простейшую операцию, например сложения, над множествами, приведенными на рис. 7.1, а и б. По правилам сложения множеств левые части будем складывать с левыми частями, а правые - с правыми (каждый элемент одного множества с каждым элементом другого множества). В результате данной операции имеем два новых множества (рис. 7.3, а, б), каждое из которых будет состоять из девяти элементов. Заметим, что и в данном случае можно подобрать пары элементов из одного и другого множества так, что каждый элемент множества Б будет превосходить соответствующий элемент множества А на число 2, т.е. можно определить линейное правило прямого (или обратного) перехода от множества А к множеству Б (рис. 3 в).
Таким образом, линейные операции над элементами однотипных множеств дают в результате элементы нового множества, обладающие теми же свойствами, что и исходные.
В геологии примером взаимнооднозначных множеств служат векторные величины, например силы, приложенные к одному блоку породы со стороны вмещающих пород. Над этими силами можно производить операции сложения, вычитания и умножения на число. Последняя операция эквивалентна увеличению или уменьшению силы в  раз. В результате будем иметь, как и в первом примере, новое множество сил, приложенных к тому же телу (множество сил А преобразуется в новое множество сил Б ).
раз. В результате будем иметь, как и в первом примере, новое множество сил, приложенных к тому же телу (множество сил А преобразуется в новое множество сил Б ).
Рассмотрим теперь чисто математические объекты. Пусть дана некоторая однородная система уравнений
 |
( 7.1) |
Так как количество неизвестных больше, чем количество уравнений, система (7.1) имеет бесконечное множество решений. Определим это множество по формулам Крамера
 |
( 7.2) |
Если теперь положить z = 1, то после подстановки его значения в формулы (7.2) получим частное решение системы (7.1), в чем можно убедиться самостоятельно:
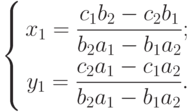 |
( 7.3) |
Положим теперь z = 5 и подставим опять в выражение (7.2). В результате получим новое решение, которое тоже удовлетворяет системе (7.1):
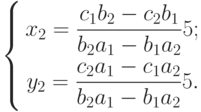 |
( 7.4) |
Сложим найденное частное решение (7.3) с другим частным решением (7.4)
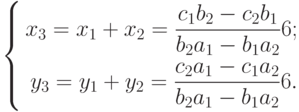 |
( 7.5) |
Мы рассмотрели примеры трех различных множеств. Объекты этих множеств различны по своей природе. Но эти множества имеют общее свойство, которое позволяет сделать вывод, что приведенные примеры есть примеры линейных пространств. Введем некоторые определения.
Определение 1. Числовым полем  называется множество чисел
называется множество чисел 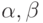 , если
, если 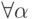 ,
,  числа
числа 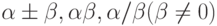 также принадлежат этому множеству.
также принадлежат этому множеству.
Определение 2. Множество  называется линейным или векторным пространством над полем
называется линейным или векторным пространством над полем  , если для любых двух его элементов
, если для любых двух его элементов  и
и  определена сумма
определена сумма 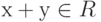 и для каждого элемента
и для каждого элемента 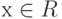 и каждого числа
и каждого числа 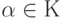 определено произведение
определено произведение  так, что выполнены следующие условия:
так, что выполнены следующие условия:
-
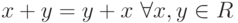 ;
; -
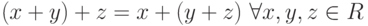 ;
; - существует такой нулевой элемент
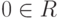 , что
, что 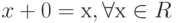 ;
; - для каждого элемента
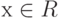 существует такой элемент -x (называется противоположным х ), что x + (-х) = 0 ;
существует такой элемент -x (называется противоположным х ), что x + (-х) = 0 ; -
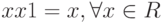 ;
; -
 ;
; -
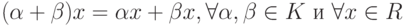 ;
; -
 .
.
Эти условия в математике называют аксиомами линейного пространства.
Традиционно элементы линейного пространства называют векторами, хотя по своей конкретной природе они могут быть вовсе не похожи на привычные для нас направленные отрезки.
Приведем еще несколько примеров линейных пространств.
- Множество многочленов степени не выше n с вещественными коэффициентами.
- Множество свободных векторов в трехмерном пространстве, рассматриваемые в аналитической геометрии. Это пространство обозначается V3.
- Множество всех матриц размером m x n.
-
n - мерное арифметическое пространство. Это множество всех упорядоченных наборов из n чисел, например х = (х1, х2, ..., хn), у = (у1, у2, ..., уn), для которых определены операции сложения и умножения на число
 по правилам:
по правилам:
Определение 3. Набор n чисел х = (х1, х2, ..., хn) называется n - мерным вектором арифметического пространства.
Определение 4. Числа х1, х2, ..., хn, составляющие n -мерный вектор х, называются координатами вектора.
Определение 5. Если координаты всех n - мерных векторов вещественные, то арифметическое пространство называют вещественным и обозначают Rn. Если координаты векторов комплексные, то пространство называют комплексным и обозначают Сn.
Очевидно, что приведенные в начале параграфа, примеры относятся к линейным пространствам. Однако не все множества образуют линейные пространства. Например, это множество многочленов степени n, в чем можно убедиться, рассмотрев сумму двух многочленов х3 - 2х2 + 1 и -х3 + 8, которые принадлежат множеству многочленов степени 3. Сумма приведенных многочленов образует многочлен второй степени, который не является элементом множества многочленов третьей степени и, следовательно, не принадлежит рассматриваемому множеству. Иными словами все многочлены всех степеней образуют, а многочлены одной какой-то степени не образуют линейное пространство.