|
Добрый день. Подскажите пожалуйста, я прошел ваш курс Введение в линейную алгебру: Информация, - сдал экзамен и у меня высветилось окно, где необходимо оформить доставку сертификата. Однако, я случайно закрыл это окно и теперь не могу найти этот подраздел, чтобы оформить доставку. Где можно это найти? |
Скалярное произведение векторов. Свойства. Векторное произведение векторов. Свойства. Смешанное произведение векторов. Свойства
Умножение
Различают несколько видов операции умножения.
1. Умножение вектора на скалярную величину. При умножении вектора  на скаляр
на скаляр  получают новый вектор
получают новый вектор  , длина (модуль) которого изменяется в
, длина (модуль) которого изменяется в  раз, а направление совпадает с направлением исходного вектора
раз, а направление совпадает с направлением исходного вектора  , если
, если 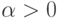 , или противоположно исходному вектору, если
, или противоположно исходному вектору, если  . В координатной форме, если a = (ax;ay;az), то b =
. В координатной форме, если a = (ax;ay;az), то b =  a=
a= 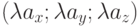 . Следовательно, операция умножения вектора на скаляр не влияет на компланарность (коллинеарность) векторов. Поэтому если несколько векторов до умножения на скаляр были компланарны (коллинеарны), то после умножения компланарность (коллинеарность) между ними сохранится.
. Следовательно, операция умножения вектора на скаляр не влияет на компланарность (коллинеарность) векторов. Поэтому если несколько векторов до умножения на скаляр были компланарны (коллинеарны), то после умножения компланарность (коллинеарность) между ними сохранится.
Заметим, что любой вектор может быть представлен как произведение единичного, коллинеарного ему вектора на модуль рассматриваемого вектора, т.е. 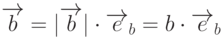 1Модуль вектора можно обозначать |\overrightarrow{b}| или просто b. Из последнего равенства следует, что
1Модуль вектора можно обозначать |\overrightarrow{b}| или просто b. Из последнего равенства следует, что  . Операция умножения вектора на скаляр обладает свойствами коммутативности и ассоциативности:
. Операция умножения вектора на скаляр обладает свойствами коммутативности и ассоциативности: 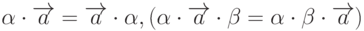 , а также свойством дистрибутивности:
, а также свойством дистрибутивности: 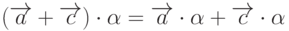 .
.
2. Скалярное произведение векторов.
Определение 14. Скалярным произведением двух векторов  и
и  называется число S, равное
называется число S, равное  . Эта операция обозначается
. Эта операция обозначается 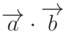 или
или 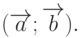
В частности, скалярный квадрат вектора равен квадрату его длины, т.е.
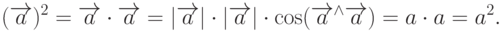
Если один из перемножаемых векторов единичный, то:

 на направление единичного вектора
на направление единичного вектора 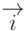 . Следовательно, любой вектор можно представить как
. Следовательно, любой вектор можно представить как 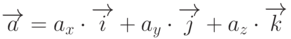 , где ax,ay,az - проекции вектора
, где ax,ay,az - проекции вектора  соответственно на оси 0х, 0у и 0z.
соответственно на оси 0х, 0у и 0z.Если вектор представлен через проекции на базисные векторы, то говорят о разложении вектора  по ортогональному базису. Из рис. 6.1 видно, что в этом случае вектор
по ортогональному базису. Из рис. 6.1 видно, что в этом случае вектор  является главной диагональю прямоугольного параллелепипеда, ребра которого параллельны осям координат и равны длинам проекций вектора
является главной диагональю прямоугольного параллелепипеда, ребра которого параллельны осям координат и равны длинам проекций вектора  на эти оси. Из этого же рисунка следует, что модуль вектора
на эти оси. Из этого же рисунка следует, что модуль вектора  численно будет равен
численно будет равен 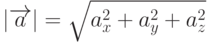 .
.
Из определения скалярного произведения следует, что любой вектор, независимо от типа, можно представить в виде:

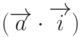 ,
, 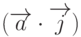 и
и  есть скалярное произведение вектора
есть скалярное произведение вектора  с ортами осей координат. Тогда из последнего равенства имеем
с ортами осей координат. Тогда из последнего равенства имеем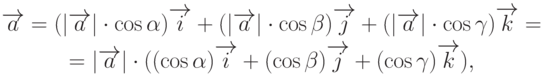
 ,
,  и
и  - углы, которые составляет вектор
- углы, которые составляет вектор  соответственно с осями 0х, 0у и 0z.
соответственно с осями 0х, 0у и 0z.Можно заметить, что скалярное произведение коммутативно и дистрибутивно, т.е.  и
и  . Можно убедиться самостоятельно в том, что всегда выполняется равенство
. Можно убедиться самостоятельно в том, что всегда выполняется равенство
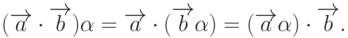
Замечание 1. Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны. Действительно, если ни один из векторов не нулевой, то, по определению скалярного произведения, последнее может быть равно нулю только тогда, когда
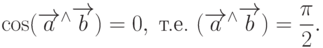
Замечание 2. 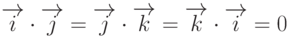 , где
, где 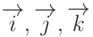 - единичные векторы (орты) осей координат 2При этом оси координат могут быть взаимноперпендикулярны (ортогональны), хотя это и не обязательно. Данное замечание выполняется и для произвольной системы координат (косоугольной, криволинейной).
- единичные векторы (орты) осей координат 2При этом оси координат могут быть взаимноперпендикулярны (ортогональны), хотя это и не обязательно. Данное замечание выполняется и для произвольной системы координат (косоугольной, криволинейной).
Замечание 3. 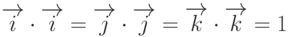 .
.
Замечание 4. Скалярное произведение векторов в координатной форме
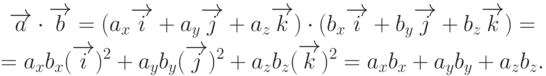
Замечание 5. Используя формулу скалярного произведения векторов  и
и  , можно найти выражение косинуса угла между этими векторами через их проекции на орты:
, можно найти выражение косинуса угла между этими векторами через их проекции на орты:
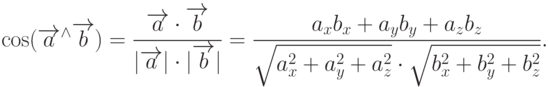
Если 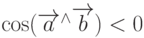 , то это значит, что угол между векторами больше 90
, то это значит, что угол между векторами больше 90  , т.е. тупой, а если
, т.е. тупой, а если 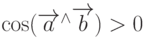 , то угол острый.
, то угол острый.
Замечание 6. Механический смысл скалярного произведения векторов. Скалярное произведение силы F на вектор перемещения S равно работе А этой силы при перемещении материальной точки по вектору S: A = FS.


