Лекция 7: Нелинейное программирование. Классификация методов нелинейного программирования. Классический метод определения условного экстремума. Метод множителей Лагранжа
Теорема 3.6 (о выпуклости допустимого множества решений). Пусть 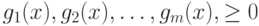 и
и  - ограничения задачи нелинейного
программирования. Если функции
- ограничения задачи нелинейного
программирования. Если функции 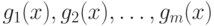 - вогнуты, то допустимое множество
- вогнуты, то допустимое множество 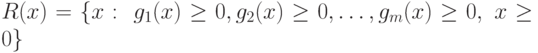 является выпуклым.
является выпуклым.
Доказательство. Для доказательства теоремы достаточно показать,
что множество  при каждом
при каждом  будет выпуклым. Тогда множество
будет выпуклым. Тогда множество  также выпукло, так как пересечение конечного числа выпуклых
множеств Ri.
также выпукло, так как пересечение конечного числа выпуклых
множеств Ri.
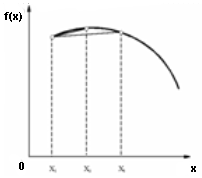
Рассмотрим некоторую вогнутую функцию  .
Выберем две произвольных точки
.
Выберем две произвольных точки  и
и 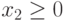 (рис.7.1).
Тогда
(рис.7.1).
Тогда  .
Поскольку
.
Поскольку 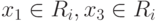 ,
то и точка x2 принадлежит Ri.
Из условия вогнутости gi следует, что
,
то и точка x2 принадлежит Ri.
Из условия вогнутости gi следует, что ![g_i[\lambda x+1 +(1 - \lambda)] \ge g_i (x_1) \lambda + (1 - \lambda) g_i(x_1) \ge 0](/sites/default/files/tex_cache/8cdaef10d8de2a0b59a1072e47b4f136.png) .
.
Следовательно, множество Ri содержит отрезок 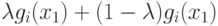 ,
и поэтому оно выпукло (рис.7.1).
,
и поэтому оно выпукло (рис.7.1).
Справедливое такое утверждение: если функции 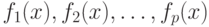 - выпуклы (вогнуты) на множестве Ri, то функция
- выпуклы (вогнуты) на множестве Ri, то функция  - также выпукла (вогнута)
при условии, что все
- также выпукла (вогнута)
при условии, что все  .
.
Рассмотрим метод поиска условного экстремума. Он состоит из следующих процедур.
1.Отыскивают множество всех
стационарных точек S1(x)
функции f(x) на выпуклом допустимом множестве R. Найденные точки далее исследуют на максимум (минимум) и
определяют точку наибольшего максимума 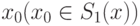 .
.
2. Переходят к исследованию точек границы S2(x) и отысканию тех из них, где f(x) достигает максимума. Этот процесс состоит в следующем. Выбирают произвольную границу, определяемую, например, условием g1(x)=0. Если функция
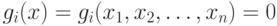 |
( 3.7) |

Обозначим через  точку границы
точку границы  ,
в которой f(x) достигает максимума.
Повторив вышеописанную процедуру по всем остальным границам,
найдем соответственно точки максимума (минимума) для всех границ
,
в которой f(x) достигает максимума.
Повторив вышеописанную процедуру по всем остальным границам,
найдем соответственно точки максимума (минимума) для всех границ 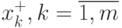 .
.
3. Непосредственным сравнением значений функции f(x) для всех точек 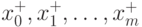 определяют точку абсолютного
максимума (минимума) xopt на множестве решений R.
определяют точку абсолютного
максимума (минимума) xopt на множестве решений R.
Такой подход требует значительных вычислительных затрат и может применяться лишь в простейших случаях при небольшом числе ограничений m и для случая сепарабельных функций g1(x), поэтому область его применения очень ограничена, и ниже рассматриваются более эффективные методы решения задач условной оптимизации.
Обобщение понятия выпуклой функции. Рассмотрим некоторые классы функций, которые не являются полностью выпуклыми, но обладают лишь отдельными их свойствами.
Определение 3.5. Пусть функция f(x) определена на непустом и выпуклом множестве R. Функция f(x) квазивыпукла, если для любых 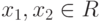 и
и ![\lambda \in [0,1]](/sites/default/files/tex_cache/ada29722c713d4d8a571d9a4ce353ae6.png) выполняется неравенство
выполняется неравенство
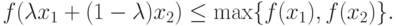 |
( 3.8) |
Функция f(x) называется квазивогнутой, если -f(x) - квазивыпуклая функция.
Из этого определения следует, что функция f(x) - квазивыпукла,
если из неравенства  следует, что f(x2)
не меньше значения функции f(x) в любой точке,
являющейся выпуклой комбинацией точек x1 и x2.
И наоборот, функция f(x) квазивогнута, если из неравенства
следует, что f(x2)
не меньше значения функции f(x) в любой точке,
являющейся выпуклой комбинацией точек x1 и x2.
И наоборот, функция f(x) квазивогнута, если из неравенства  следует, что f(x1)
не больше значения f(x) в любой точке, которая есть
выпуклой комбинацией точек x1 и x2.
следует, что f(x1)
не больше значения f(x) в любой точке, которая есть
выпуклой комбинацией точек x1 и x2.
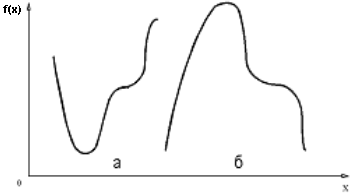
На рис. 7.2 приведены примеры квазивыпуклых и квазивогнутых функций, где а - квазивыпуклая, б - квазивогнутая функции.
Введем понятия строгой квазивыпуклости и квазивогнутости.
Определение 3.6. Пусть функция f(x) определена на непустом и выпуклом множестве R. Функция f(x) строго квазивыпукла, если для любых 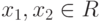 таких, что
таких, что  и
и  выполняется неравенство
выполняется неравенство
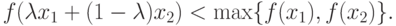 |
( 3.9) |
Функция f(x) называется строго квазивогнутой, если -f(x) - строго квазивыпуклая функция. На рис. 7.3 изображены: а, б - строго квазивыпуклые функции, в - квазивогнутая функция. Из приведенного определения следует, что любая выпуклая функция является в тоже время и строго квазивыпуклой.
Строго квазивыпуклые и квазивогнутые функции играют важную роль в нелинейном программировании, поскольку для них локальный минимум и локальный максимум являются глобальным минимумом и максимумом соответственно.
Утверждение.
Пусть f(x) - строго квазивыпуклая
функция. Рассмотрим задачу минимизаци f(x) при условии, что  , где R - непустое выпуклое множество в E(n). Пусть
, где R - непустое выпуклое множество в E(n). Пусть  - точка локального
минимума рассматриваемой
задачи. Тогда она является и точкой глобального минимума.
- точка локального
минимума рассматриваемой
задачи. Тогда она является и точкой глобального минимума.
Доказательство. Предположим противное, то есть пусть
существует точка  , для которой
, для которой 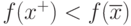 .
Поскольку R - выпуклое, то точка
.
Поскольку R - выпуклое, то точка  при любой
при любой  .
Так как
.
Так как  - точка локального минимума, то
- точка локального минимума, то
![f(\overline{x}) \le f [\lambda x^+ + (1-\lambda) \overline{x} ]](/sites/default/files/tex_cache/e0581d26bbb481735e73da2766828948.png) |
( 3.10) |
 для некоторого
для некоторого 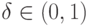 .
.Поскольку f(x) - квазивыпуклая
функция и выполняется
неравенство 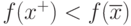 , то мы получим, что
, то мы получим, что ![f[\lambda x^+ + (1-\lambda)\overline{x} ]< f(\overline{x})](/sites/default/files/tex_cache/7b904c089ffec981102264d722d31586.png) при всех
при всех  .
Однако это соотношение противоречит (3.10).
.
Однако это соотношение противоречит (3.10).
Заметим, что строго квазивыпуклые и квазивогнутые функции называются унимодальными.