исследование операций (личная):

Введение в математическое программирование
[+]
Опубликован: 09.07.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Донецкий национальный технический университет

Лекция 7: Нелинейное программирование. Классификация методов нелинейного программирования. Классический метод определения условного экстремума. Метод множителей Лагранжа

A
|
версия для печати
< Лекция 6 || Лекция 7: 1234 || Лекция 8 >

2. Классификация методов нелинейного программирования

Для решения задачи нелинейного программирования было предложено много методов, которые можно классифицировать по различным признакам.

По количеству локальных критериев в целевой функции методы нелинейного программирования делятся на:

  • однокритериальные,
  • многокритериальные.

По длине вектора \overline{X} методы делятся на:

  • однопараметрические или одномерные (n=1),
  • многопараметрические или многомерные (n>1).

По наличию ограничений методы нелинейного программирования делятся на:

  • без ограничений (безусловная оптимизация),
  • с ограничениями (условная оптимизация).

По типу информации, используемой в алгоритме поиска экстремума методы делятся на:

  • методы прямого поиска, т.е. методы, в которых при поиске экстремума целевой функции используются только ее значения;
  • градиентные методы первого порядка, в которых при поиске экстремума функции используются значения ее первых производных;
  • градиентные методы второго порядка, в которых при поиске экстремума функции наряду с первыми производными используются и вторые производные.

Ни один метод нелинейного программирования не является универсальным. В каждом конкретном случае необходимо приспосабливать применяемый метод к особенностям решаемой задачи.

3. Классический метод определения условного экстремума

Задача нелинейного программирования (задача НП) в общем виде формулируется так:

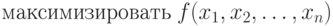
\text{максимизировать} \; f(x_1,x_2,\ldots,x_n)
при ограничениях
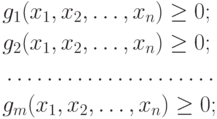
\begin{align*} & g_1(x_1,x_2,\ldots,x_n) \ge 0 ; \\ & g_2(x_1,x_2,\ldots,x_n) \ge 0 ; \\ & \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\ & g_m(x_1,x_2,\ldots,x_n) \ge 0 ; \end{align*}
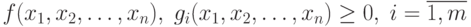где функции f(x_1,x_2,\ldots,x_n), \; g_i(x_1,x_2,\ldots,x_n) \ge 0, \; i = \overline{1,m} нелинейны.

В отличие от задачи ЛП для задач НП нет универсального метода решения.

В задаче ЛП допустимое множество R всегда является выпуклым с конечным числом крайних точек. Поэтому воспользовавшись симплекс-методом и перебрав только крайние точки, можно за конечное число шагов найти оптимальное решение. В задачах НП, наоборот, выпуклость допустимого множества и конечность числа его крайних точек совсем необязательны. Это и служит причиной основной трудности решения задач НП.

Для определения условного экстремума (то есть экстремума при ограничениях) можно воспользоваться методами дифференциального исчисления, когда функция 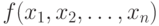f(x_1,x_2,\ldots,x_n) имеет не ниже второй производной. Рассмотрим некоторые важные понятия и теоремы классического анализа, которые лежат в основе классических методов поиска условного экстремума .

Теорема 3.1 (теорема существования экстремума). Если 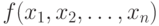f(x_1,x_2,\ldots,x_n) - непрерывная функция, определенная на замкнутом и ограниченном множестве, то она достигает на этом множестве, по крайней мере один раз, своих максимального и минимального значений>.

Следующая теорема определяет возможные местоположения максимума (или минимума).

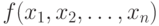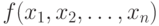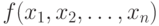Теорема 3.2. Если f(x_1,x_2,\ldots,x_n) является непрерывной функцией нескольких переменных, определенной на допустимом множестве R, то максимальное значение f(x_1,x_2,\ldots,x_n), если оно существует, достигается в одной или нескольких точках, которые принадлежат одному из следующих множеств: 1) S1 - множество стационарных точек ; 2) S2 - множество точек границы ; 3) S3 - множество точек, где функция f(x_1,x_2,\ldots,x_n) недифференцируема.

Определение 3.1. Множество точек S1(x1, x2, ..., xn) функции f(x) называется множеством стационарных точек, если они удовлетворяют условию

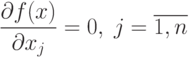\frac{\partial f(x)}{\partial x_j} = 0, \; j=\overline{1,n} ( 3.1)

Определение 3.2. Функция f(x) достигает локального максимума в точке 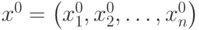x^0=\left( x_1^0, x_2^0, \ldots, x_n^0 \right), если для всех точек x, лежащих в малой окрестности точки \left[ x_1^0, x_2^0, \ldots, x_n^0 \right] имеет место неравенство

f \left( x_1^0, x_2^0, \ldots, x_n^0 \right) \ge f \left( x_1, x_2, \ldots, x_n \right) ( 3.2)

Определение 3.3. Функция f(x) достигает глобального (абсолютного) максимума в точке x0, если для всех точек x \in R справедливо неравенство

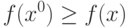
f(x^0) \ge f(x)

Для нахождения стационарных точек функции f(x) можно использовать следующую теорему.

Теорема 3.3. Пусть 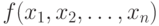f(x_1,x_2,\ldots,x_n) дифференцируема в некоторой допустимой области R. Если в некоторой внутренней точке 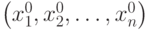\left( x_1^0, x_2^0, \ldots, x_n^0 \right) области R функция f(x) достигает относительного максимума, то

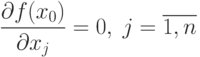\frac{\partial f(x_0)}{\partial x_j} = 0, \; j=\overline{1,n} ( 3.3)

Для того чтобы определить, являются ли найденные стационарные точки точками максимума или минимума, необходимо исследовать функцию 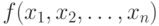f ( x_1, x_2, \ldots, x_n ) в окрестности стационарных точек и определить, является она выпуклой или вогнутой.

Определение 3.4. Пусть R - выпуклое множество точек n - мерного пространства. Функция f, определенная на R, называется выпуклой вверх, если для любой пары точек 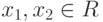x_1, x_2 \in R и произвольного 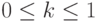0 \le k \le 1 выполняется неравенство

f[kx_1+(1-k)x_2] \ge kf(x_1)+(1-k)f(x_2) ( 3.4)

Если

f[kx_1+(1-k)x_2] \le kf(x_1)+(1-k)f(x_2) ( 3.5)
то функция называется вогнутой.

Если (3.4) или (3.5) выполняются как строгие неравенства, то функция называется строго вогнутой или строго выпуклой соответственно.

Критерий выпуклости и вогнутости функции n - переменных можно сформулировать в виде следующей теоремы.

Теорема 3.4. Дифференцируемая функция f(x) строго вогнутая в некоторой окрестности точки 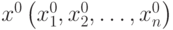x^0 \left( x_1^0, x_2^0, \ldots, x_n^0 \right), если выполняются следующие условия:

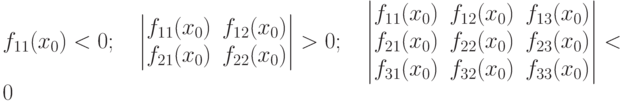f_{11}(x_0) < 0; \quad \begin{vmatrix} f_{11}(x_0) & f_{12}(x_0) \\ f_{21}(x_0) & f_{22}(x_0) \end{vmatrix} > 0 ; \quad \begin{vmatrix} f_{11}(x_0) & f_{12}(x_0) & f_{13}(x_0) \\ f_{21}(x_0) & f_{22}(x_0) & f_{23}(x_0) \\ f_{31}(x_0) & f_{32}(x_0) & f_{33}(x_0) \end{vmatrix} < 0 ( 3.6)

И так далее, то есть если знаки определителей чередуются начиная с < 0, где

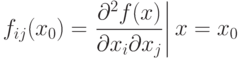
f_{ij}(x_0) = \left. \frac{\partial^2 f(x)}{\partial x_i \partial x_j} \right| x=x_0

Функция f(x) строго выпукла в окрестности точки x0, если все определители (выписанные выше) положительные.

Имеет место следующая теорема.

Теорема 3.5. Для того чтобы в точке x0 достигался внутренний относительный минимум, достаточно, чтобы эта точка была стационарной, а самая функция в окрестности точки x0 была строго выпуклой.

Справедливо следующее утверждение: если f(x) строго выпуклая (вогнутая) функция на всем множестве решений R, то f имеет только один относительный минимум (максимум), который является и абсолютным.

Дальше >>
< Лекция 6 || Лекция 7: 1234 || Лекция 8 >

Вопросы и ответы

вопросов: 0