Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Донецкий национальный технический университет

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать программу

Лекция 8: Задача нелинейного программирования при ограничениях – неравенствах. Седловая точка и задача нелинейного программирования. Применение теоремы Куна – Таккера для задачи выпуклого программирования

A

|

версия для печати

Аннотация: В данной лекции рассматривается задача нелинейного программирования при наличии ограничений в виде неравенств, в частности, ее форма записи, преимущества и недостатки в сравнении с задачей, имеющей ограничения – равенства, основные понятия и свойства. Кроме того, вводится понятие седловой точки и выясняется ее роль в задаче нелинейного программирования. При этом особое место отводится теореме Куна – Таккера, а также затрагивается вопрос применения данной теоремы к задаче выпуклого программирования.

Ключевые слова: активное ограничение, допустимая область, гиперплоскость, входящий вектор, условия регулярности ограничений, линейная независимость векторов-градиентов, оптимальное решение задачи, нелинейное программирование, функция Лагранжа, множители Лагранжа, условия дополняющей нежесткости, допустимое множество решений, условие регулярности Слейтера, седловая точка функции Лагранжа, неравенство для седловой точки, задача выпуклого программирования, задача вогнутого программирования

1. Задача нелинейного программирования при ограничениях – неравенствах

Теорема Куна-Таккера. Рассмотрим случай задачи с ограничениями-неравенствами:

$\text{минимизировать} \; f(x)$

( 1.1)

при ограничениях

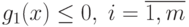$g_1(x) \le 0, \; i=\overline{1,m}$

( 1.2)

В точке минимума x⁺ неравенства g_i(x) могут выполняться как равенства или строгие неравенства.

Ограничение g_i(x) называется активным в точке x⁺, если оно выполняется в ней как строгое равенство, то есть если g_i(x₊)=0

Используя геометрические свойства допустимой области, найдем необходимые условия экстремума для задач минимизаци с ограничениями. Для этого сначала рассмотрим случай, когда все g_i(x) линейны. Итак, пусть требуется найти $\min f(x)$ при условии

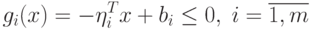
$g_i(x) = - \eta_i^T x + b_i \le 0, \; i =\overline{1,m}$

Здесь каждое ограничение (1.3) определяет полупространство в Rⁿ. Допустимая область S задана пересечением m полупространств, определяемых неравенствами (1.3), и следовательно, является выпуклым многогранником. Вектор $\eta_i$ является нормалью к гиперплоскости, определяемой уравнением g_i(x)=0, и направлен внутрь области S.

Пусть точка x⁺ является точкой минимума задачи (1.1) с ограничениями (1.3). Обозначим множество индексов активных ограничений через

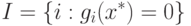$I=\lbrace i: g_i(x^*)=0 \rbrace$

( 1.4)

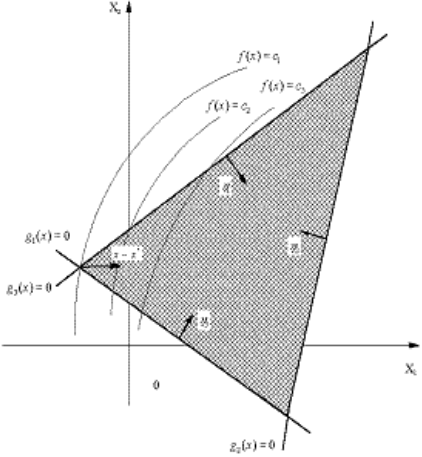
Например, на рис.8.1 приведен пример минимизации с линейными ограничениями. Выберем любую допустимую точку x из S. Вектор x-x⁺ направлен из x⁺ внутрь области S. Такой вектор будем называть входящим. Для этого вектора с учетом того, что $\eta_i = - \nabla g_i (x^*)$ , можно записать следующее условие:

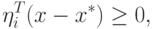
$\eta_i^T(x-x^*) \ge 0,$

или

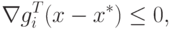$\nabla g_i^T (x-x^*) \le 0,$

( 1.5)

для всех $i \in I$ и $x \in S$ .

Рис. 8.1.

Таким образом, входящий вектор x определяет допустимое направление перемещения из точки x⁺. Но так как f(x) минимальна в точке x⁺, то при любом x-x⁺, удовлетворяющем (1.5), будем иметь:

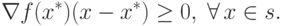$\nabla f(x^*)(x-x^*) \ge 0, \; \forall \, x \in s.$

( 1.6)

Применим теперь теорему, которая есть следствием леммы Фаркаша. Из условий (1.5), (1.6) на основании леммы Фаркаша следует, что существует множество неотрицательных скаляров $\{ \lambda_i \} \ge 0$ , для которых

$\nabla f(x^*) = \sum_{i \in I} \lambda_i \eta_i (x) = - \sum_{i \in I} \lambda_i \nabla g_i (x^*).$

( 1.7)

Отметим, что уравнение (1.7) аналогично (4.15). Если принять, что 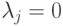$\lambda_j = 0$ при $j \in I$ (то есть для неактивных ограничений), (1.7) можно переписать в виде

$\nabla f(x^*) = \sum_{i = 1}^m \lambda_i \eta_i (x) = - \sum_{i = 1}^m \lambda_i \nabla g_i (x^*).$

( 1.8)

Кроме того, получим, что

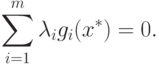$\sum_{i = 1}^m \lambda_i g_i (x^*) = 0.$

( 1.9)

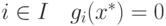поскольку при $i \in I \quad g_i(x^*)=0$ , а при $j \notin I \quad \lambda_i = 0$ . Поэтому уравнения ограничений можно включить в целевую функцию следующим образом:

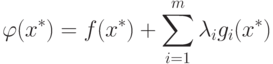$\varphi(x^*) = f(x^*) + \sum_{i=1}^m \lambda_i g_i(x^*)$

( 1.10)

Следовательно, x⁺ удовлетворяет следующим условиям:

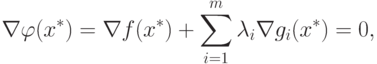$\nabla \varphi(x^*) = \nabla f(x^*) + \sum_{i=1}^m \lambda_i \nabla g_i(x^*) = 0,$

( 1.11)

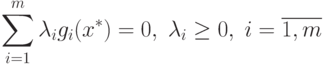$\sum_{i=1}^m \lambda_i g_i(x^*) = 0, \; \lambda_i \ge 0, \; i=\overline{1,m}$

( 1.12)

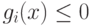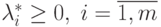При рассмотрении задачи минимизации f(x) при условиях $g_i(x) \le 0$ может случиться так, что не будет существовать таких $\lambda_i^* \ge 0, \; i=\overline{1,m}$ , для которых без дополнительных предположений о природе функций были бы справедливы уравнения (1.9), (1.10), где x⁺ - оптимальное решение. Эти дополнительные предположения называют условиями регулярности ограничений. В частности, в рассмотренном случае, в качестве таких условий использовали линейную независимость векторов-градиентов ограничений $\nabla g_i (x^*), i=\overline{1,m}$ .

Дальше >>

Введение в математическое программирование

1. Задача нелинейного программирования при ограничениях – неравенствах

Вопросы и ответы

Авторизоваться

Введение в математическое программирование

1. Задача нелинейного программирования при ограничениях – неравенствах

Вопросы и ответы