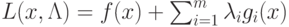Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Донецкий национальный технический университет

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать программу

Лекция 8: Задача нелинейного программирования при ограничениях – неравенствах. Седловая точка и задача нелинейного программирования. Применение теоремы Куна – Таккера для задачи выпуклого программирования

A

|

версия для печати

2. Седловая точка и задача нелинейного программирования

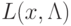Рассмотрим функцию Лагранжа $L(x, \Lambda)=f(x)+\sum_{i=1}^m \lambda_i g_i (x)$

Определение 2.1. Пара векторов $x^*, \Lambda^*$ называется седловой точкой функции Лагранжа $L(x, \Lambda)$ , если при всех 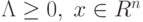$\Lambda \ge 0, \; x \in R^n$ выполняется условие

$L(x^*, \Lambda) \le L(x^*, \Lambda^*) \le L(x, \Lambda^*)$

( 2.1)

Неравенство (2.1) называют неравенством для седловой точки. Очевидно, что в седловой точке выполняется условие

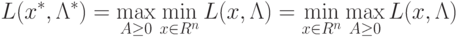$L(x^*, \Lambda^*) = \max_{A \ge 0} \min_{x \in R^n} L(x, \Lambda) = \min_{x \in R^n} \max_{A \ge 0} L(x, \Lambda)$

( 2.2)

Между понятием седловой точки функции Лагранжа 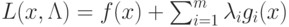$L(x, \Lambda) = f(x) + \sum_{i=1}^m \lambda_i g_i (x)$ и решением задачи НП существует взаимосвязь, которая устанавливается в следующей теореме.

Теорема 2.1. Пусть f(x) и все g_i(x) выпуклы и функции g_i(x) удовлетворяют условию регулярности Слейтера. Вектор x⁺ является решением задачи НП (1.1), (1.2) тогда и только тогда, когда существует такой вектор $\Lambda^* \ge 0$ , что

$L(x^*, \Lambda) \le L(x^*, \Lambda^*) \le L(x, \Lambda^*)$

( 2.3)

и

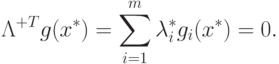$\Lambda^{+T} g(x^*) = \sum_{i=1}^m \lambda_i^* g_i (x^*) = 0.$

( 2.4)

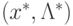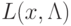Доказательство. Сначала докажем достаточность условий теоремы. Пусть $(x^*, \Lambda^*)$ - седловая точка функции $L(x, \Lambda)$ . Тогда из правого неравенства (1.24) получим

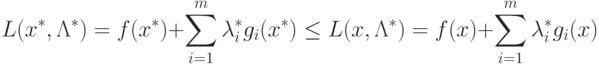$L(x^*, \Lambda^*) = f(x^*) + \sum_{i=1}^m \lambda_i^* g_i (x^*) \le L(x, \Lambda^*) = f(x) + \sum_{i=1}^m \lambda_i^* g_i (x)$

( 1.25)

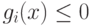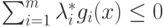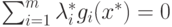Поскольку $\lambda_i^* \ge 0$ , а $g_i(x) \le 0$ , то $\sum_{i=1}^m \lambda_i^* g_i (x) \le 0$ . Вместе с тем $\sum_{i=1}^m \lambda_i^* g_i (x^*) = 0$ согласно с (2.4). Поэтому из (2.3) следует неравенство

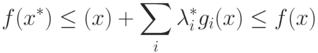
$f(x^*) \le (x) + \sum_i \lambda_i^* g_i (x) \le f(x)$

для всех x, удовлетворяющих ограничениям задачи НП. Таким образом, x^* - оптимальное решение задачи НП.

Перейдем к доказательству необходимости. Допустим, что x^* - оптимальное решение задачи НП. Заметим, что система

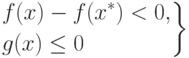$\left. \begin{aligned} & f(x) - f(x^*) < 0, \\ & g(x) \le 0 \end{aligned} \right\}$

( 2.6)

не имеет решения, так как x^* - точка минимума задачи НП. Отсюда следует также, что не имеет решений и следующая система:

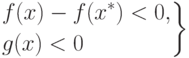$\left. \begin{aligned} & f(x) - f(x^*) < 0, \\ & g(x) < 0 \end{aligned} \right\}$

( 2.7)

Тогда согласно теореме Фана существуют такие 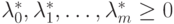$\lambda_0^*, \lambda_1^*, \ldots, \lambda_m^* \ge 0$ , что

$\lambda_0^* \left[ f(x) - f(x^*) \right] + \sum_{i=1}^m \lambda_i^* g_i (x) \ge 0.$

( 2.8)

Поскольку

$\lambda_i^* \ge 0, \quad g_i(x^*) \le 0, \forall i,$

то

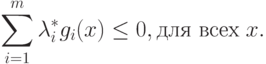$\sum_{i=1}^m \lambda_i^* g_i (x) \le 0, \text{для всех} \; x .$

( 2.9)

Если же в (2.8) положить x=x^*, то получим

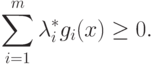$\sum_{i=1}^m \lambda_i^* g_i (x) \ge 0.$

( 2.10)

Сравнив (2.9) с (2.10), получим

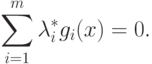$\sum_{i=1}^m \lambda_i^* g_i (x) = 0.$

( 2.11)

Тогда из уравнений (2.8) и (2.11) получим

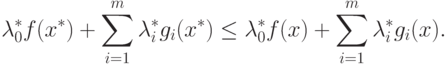$\lambda_0^* f(x^*) + \sum_{i=1}^m \lambda_i^* g_i (x^*) \le \lambda_0^* f(x) + \sum_{i=1}^m \lambda_i^* g_i (x).$

( 2.12)

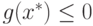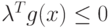Таким образом доказано правое неравенство для седловой точки. Поскольку $g(x^*) \le 0$ , то $\lambda^T g(x) \le 0$ при любом $\lambda \ge 0$ . Следовательно,

$\lambda_0^* f(x^*) + \Lambda^T g(x^*) \le \lambda_0^* f(x^*) + \Lambda^{*T} g(x^*).$

( 2.13)

Разделив обе части (2.13) на 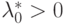$\lambda_0^* > 0$ , получим левое неравенство для седловой точки:

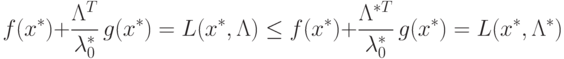
$f(x^*) + \frac{\Lambda^T}{\lambda_0^*} \, g(x^*) = L(x^*, \Lambda) \le f(x^*) + \frac{\Lambda^{*T}}{\lambda_0^*} \, g(x^*) = L(x^*, \Lambda^*)$

Таким образом, теорема доказана.

Чтобы обеспечить условие 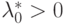$\lambda_0^* > 0$ , необходимо предположить существования условия регулярности Слейтера. В самом деле, пусть $\lambda_0^* = 0$ . Тогда выражение (2.12) примет вид

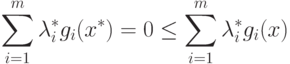$\sum_{i=1}^m \lambda_i^* g_i (x^*) = 0 \le \sum_{i=1}^m \lambda_i^* g_i (x)$

( 2.14)

Вместе с тем условие регулярности Слейтера утверждает, что существует такой вектор x, что g(x)<0, и, следовательно, 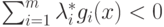$\sum_{i=1}^m \lambda_i^* g_i (x) < 0$ . Так как это противоречит уравнению (2.14), то предположения теоремы вместе с условием регулярности Слейтера обеспечивает ее справедливость.

Таким образом, при выполнении условий теоремы 2.1 задача НП становится эквивалентной задаче отыскания седловой точки функции Лагранжа.

Дальше >>

Введение в математическое программирование

2. Седловая точка и задача нелинейного программирования

Вопросы и ответы

Авторизоваться

Введение в математическое программирование

2. Седловая точка и задача нелинейного программирования

Вопросы и ответы