НОУ ИНТУИТ | Введение в математическое программирование. Лекция 6: Двойственный симплекс – метод. Исследование моделей задач линейного программирования на чувствительность

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Донецкий национальный технический университет

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать программу

Итак, последовательные переходы от одного сопряженного базиса к другому производят до тех пор , пока не получат решение задачи или не установят ее неразрешимость. Каждый переход от одного псевдоплана к другому составляет одну итерацию (один шаг) двойственного симплекс-метода.

Каждая итерация содержит два этапа. На первом этапе выясняют, не является ли псевдоплан оптимальным планом прямой задачи, и если нет, то разрешима ли задача. Для этого необходимо вычислить 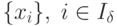$\{ x_i \}, \; i \in I_{\delta}$ и установить их знаки. Второй этап состоит в осуществлении элементарного преобразования - (одной итерации) метода полного исключения Жордана-Гауса, приводящего к новому псевдоплану с меньшим значением целевой функции.

Описание алгоритма. Задача ЛП должна быть задана в канонической форме (1.1), (1.2) или сведена к ней. Отыскивают сопряженный базис двойственной задачи и обозначают его $\{ A_i \}, i \in I_{\delta}$ . Разложим А₀ по векторам базиса А_і1,.,А_іm в соответствии с (1.9) и найдем псевдоплан $\{ х_{i0} \}, i \in I_{\delta}$ прямой задачи.

Исследуем знаки {х_i0}. Если имеет место случай 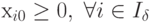$х_{i0} \ge 0, \; \forall i \in I_{\delta}$ , то начальный псевдоплан является оптимальным планом прямой задачи. При наличии отрицательных компонент {х_i0} вычисляем коэффициенты разложения векторов A_j по векторами сопряженного базиса {х_ij} в соответствии с (1.8).

Если для некоторого r такого, что х_r0<0, все $х_{rj} \ge 0$ то задача не разрешима (второй случай), и на этом процесс вычислений заканчивается.

Если имеет место третий случай (то есть для каждого r такого, что х_r0<0, по крайней мере одна из компонент х_rj<0 ), то переходим к второму этапу. С этой целью составляют таблицу k -й итерации (аналогичную симплекс-таблице), которая состоит (m+2) строк и (n+1) -го столбца (табл. 6.1).

Столбец В_x таблицы, как обычно, содержит векторы {A_i} базиса псевдоплана хk, а столбец А₀ - базисные компоненти псевдоплана {х_i0(k)}. Строка (m+1) -индексная, ее заполняют параметрами 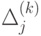$\Delta_j^{(k)}$ , являющимися оценками векторов А_j:

$\Delta_j = a_{0j} = \sum_{i \in I_{\delta}} c_i x_{ij} - c_j ,$

величина - значение целевой функции при псевдоплане

$\Delta_0 = \sum_{i \in I_{\delta}} c_i x_{i0}^{(K)}.$

Итерацию k завершают заполнением главной части таблицы (от первой до (m+1) -й строк).

Таблица 6.1.
C			C₁	C₂	.	C_j	.	C_n
	B_x	A₀	A₁	A₂	.	A_j	.	A_n
C₁	X₁	X₁₀	X₁₁	X₁₂	.	X_1j	.	X_1n
C₂	X₂	X₂₀	X₂₁	X₂₂	.	X_2j	.	X_2n
.	.	.	.	.	.	.	.	.
C_i	X_i	X_i0	X_i1	X_i2	.	X_ij	.	X_in
.	.	.	.	.	.	.	.	.
C_m	X_m	X_m0	X_m1	X_m2	.	X_mj	.	X_mn
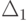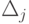	$\Delta$	$\Delta_0$	$\Delta_1$	$\Delta_2$	.	$\Delta_j$	.	$\Delta_n$
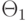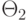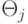	$\Theta$		$\Theta_1$	$\Theta_2$	.	$\Theta_j$	.

На первом этапе (k+1) -и итерации выясняют, имеет ли место первый, второй или третий случай.

В третьем случае переходим ко второму этапу. Сначала определяют вектор А_r, который необходимо вывести из базиса. Его индекс r определяют из условия

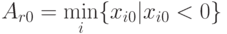$A_{r0} = \min_i \{ x_{i0} | x_{i0} < 0 \}$

( 1.14)

т.е. по максимальной по модулю отрицательной компоненте базисного решения.

Затем заполняют элементы (m+2) -й строки, которые вычисляют по формуле

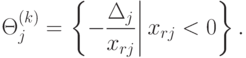$\Theta_j^{(k)} = \left. \left\{ - \frac{\Delta_j}{x_{rj}} \right| x_{rj} < 0 \right\}.$

( 1.15)

В строке $\Theta$ заполняют лишь те позиции, для которых x_rj<0. Вектор А_l, который должен быть введен в базис, находят из условия

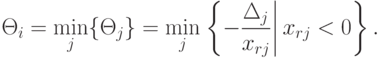
$\Theta_i = \min_j \{ \Theta_j \} = \min_j \left. \left\{ - \frac{\Delta_j}{x_{rj}} \right| x_{rj} < 0 \right\}.$

Определив направляющую строку r и столбец l, вычисляют элементы главной части таблицы (k+1) -й итерации по рекуррентным соотношениям

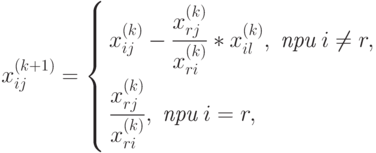$x_{ij}^{(k+1)} = \left\{ \begin{aligned} & x_{ij}^{(k)} - \frac{x_{rj}^{(k)}}{x_{ri}^{(k)}} * x_{il}^{(k)}, \; \textit{при} \; i \neq r , \\ & \frac{x_{rj}^{(k)}}{x_{ri}^{(k)}}, \; \textit{при} \; i = r , \end{aligned} \right.$

( 1.15)

где x_ri - направляющий элемент преобразования.

Вычислительная схема алгоритма двойственного симплекс-метода похожа на вычислительную схему симплекс-метода. Аналогичны и формы таблиц.

Различие между методами заключается в том, что при симплекс-методе производят последовательный переход от одного допустимого базисного решения (опорного плана) задачи к другому, а при двойственном симплеск-методе - переход от одного псевдоплана к другому.

Формальное различие между вычислительными схемами этих методов проявляется только в правилах перехода от одного базиса к другому, а также в признаках оптимальности и неразрешимости задачи. В симплекс-методе сначала определяют вектор, вводимый в базис, а затем - вектор,исключаемый из базиса, а в двойственном симплекс-методе этот порядок - обратный.

Отметим некоторые важные свойства двойственного симплекс-метода.

В отличие от прямого симплекс-метода, двойственный симплекс-метод не требует нахождения начального базисного решения ( опорного плана ), а поиск начального псевдоплана часто может оказаться легче, чем поиск ДБР.

Рассмотрим, например, типичную задачу минимизации

$\sum_{j=1}^n c_j x_j$

( 1.17)

при условиях

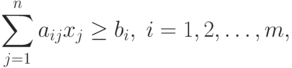$\sum_{j=1}^n a_{ij} x_j \ge b_i, \; i=1,2,\ldots,m ,$

( 1.18)

$x_j \ge 0 ,$

( 1.19)

$c_j \ge 0.$

( 1.20)

Для задачи такого вида найти сразу начальный опорный план нельзя, и поэтому необходимо применить метод искусственных переменных и выполнить значительный объем вычислений. В то же время псевдоплан находится почти автоматически. Действительно, перейдем от (1.17) - (1.19) к эквивалентной задаче в расширенной форме, введя свободные переменные x_n+1, x_n+2, ., x_n+m...

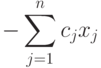$-\sum_{j=1}^n c_j x_j$

( 1.21)

при условиях

$\sum_{j=1}^n a_{ij} x_j - 1x_{n+i} = b_i, \; i= \overline{1,m}$

( 1.22)

Запишем ограничения двойственной задачи

$\sum_{i=1}^m a_{ij} y_j \ge - c_j, \; j= \overline{1,n}$

( 1.23)

$-y_i \ge 0, \; i= \overline{1,m}$

( 1.24)

Из неравенств (1.23) - (1.24) видим, что поскольку решение y_i при i=1,m удовлетворяет всем ограничениям (1.23), то сопряженный базис образуют векторы A_n+1,A_n+2,...,A_n+m при свободных переменных. При этом начальный псевдоплан такой:

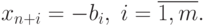
$x_{n+i} = -b_i, \; i= \overline{1,m}.$

Итак, для задачи вида (1.17) - (1.18) пpи условии (1.20) применение двойственного симплес-метода оказывается предпочтительнее в сравнении с прямым.

Двойственный симплекс-метод позволяет в процессе итерации добавлять новые дополнительные ограничения к уже найденному некоторому промежуточному решению. Это важное его свойство широко используется при решении задач целочисленного программирования.

Дальше >>

Авторизоваться

Введение в математическое программирование

Лекция 6: Двойственный симплекс – метод. Исследование моделей задач линейного программирования на чувствительность

Вопросы и ответы