Лекция 6: Двойственный симплекс – метод. Исследование моделей задач линейного программирования на чувствительность
2. Исследование моделей задач линейного программирования на чувствительность
Теория двойственности позволяет анализировать модели ЛП на чувствительность. Рассмотрим обычную задачу ЛП в виде
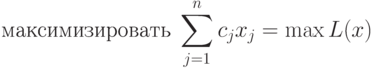 |
( 2.1) |
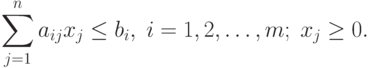 |
( 2.2) |
Напомним ее экономическую интерпретацию. Целевая функция L(x) - это доход от реализации плана производства x ; aij - интенсивность расходования i -го ресурса при j -м способе производства; bi - имеющийся уровень i -го ресурса.
1. Варьирование ограниченных ресурсов. Предположим, что величины ресурсов b=|| bi || варьируются. Тогда возникают вопросы: при каких вариациях правых частей ограничений найденный оптимальный план x0 не изменяется; как эти вариации влияют на функцию максимального дохода Lmax? Ответ на эти вопросы дает анализ соответствующей задачи ЛП на чувствительность.
Пусть ограничение bi получают некоторые
вариации 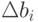 , что приводит к вариациям плана
, что приводит к вариациям плана  и функции
и функции 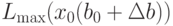 . Предположим,
эти вариации
. Предположим,
эти вариации 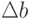 таковы, что план
таковы, что план 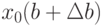 остается допустимым (т.е.
удовлетворяет условию неотрицательности). Найдем отношения приращения
остается допустимым (т.е.
удовлетворяет условию неотрицательности). Найдем отношения приращения
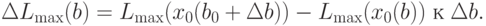
Имеем
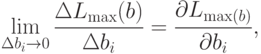 |
( 2.3) |
Вспомним, что в соответствии с основной теоремой двойственности
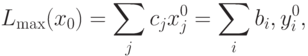 |
( 2.4) |
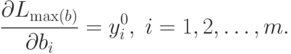 |
( 2.4) |
Таким образом, оптимальные
значения двойственных переменных 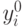 определяют вклад каждого ресурса в доход Lmax при оптимальном решении x0.
Эта величина численно равна дополнительному доходу при увеличении i -го
ресурса b_i на единицу при условии, что ресурсы используются оптимальным
образом.
определяют вклад каждого ресурса в доход Lmax при оптимальном решении x0.
Эта величина численно равна дополнительному доходу при увеличении i -го
ресурса b_i на единицу при условии, что ресурсы используются оптимальным
образом.
Итак, величины 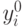 служат показателями важности соответствующих
ресурсов для системы. Чем большее значение
служат показателями важности соответствующих
ресурсов для системы. Чем большее значение 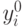 при некотором i, тем существеннее вклад i -го ресурса в функцию
максимального дохода Lmax и тем выгоднеее его увеличение.
Если для некоторого
при некотором i, тем существеннее вклад i -го ресурса в функцию
максимального дохода Lmax и тем выгоднеее его увеличение.
Если для некоторого 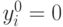 , то i -й ресурс не является
существенным ограничением для системы.
, то i -й ресурс не является
существенным ограничением для системы.
Обозначим через Ax матрицу оптимального базиса задачи ЛП при векторе ресурсов b. Очевидно соответствующее оптимальное решение
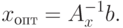
Предположим, что мы изменили вектор ресурсов b=|| bi ||
на 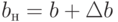 и хотим узнать, как это повлияет на
оптимальное решение. Для этого найдем новое соответствующее базисное решение
и хотим узнать, как это повлияет на
оптимальное решение. Для этого найдем новое соответствующее базисное решение
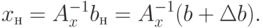
Если все компоненты 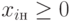 , то это решение
, то это решение ![x_{\text{н}} = [x_{i\text{н}}]](/sites/default/files/tex_cache/61c1977ec42689dc277aa3f9a7b7a84f.png) оптимально (т.е. оптимальный
базис не изменился). В противном случае нужно произвести поиск нового
решения, для этого можно применить двойственный
симплекс-метод, начиная
с текущего базисного решения
оптимально (т.е. оптимальный
базис не изменился). В противном случае нужно произвести поиск нового
решения, для этого можно применить двойственный
симплекс-метод, начиная
с текущего базисного решения 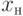 .
.
2. Варьирование целевой функции. Теперь рассмотрим случай, когда варьируются коэффициенты {cj}, j= 1,2,.,n.... Попытаемся выяснить условия, при которых найденный ранее оптимальный план останется оптимальным при таких вариациях.
Пусть вариациям 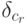 подвергнется коэффициент
подвергнется коэффициент 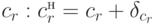 .
Обозначим через Jб, Jнеб множество
индексов базисных и небазисных векторов в оптимальном плане x0 соответственно.
.
Обозначим через Jб, Jнеб множество
индексов базисных и небазисных векторов в оптимальном плане x0 соответственно.
Найдем значения оценок 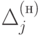 после
вариации cr для двух случаев:
после
вариации cr для двух случаев:
1) 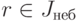 тогда
тогда 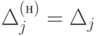 для всех
для всех 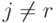 ;
;
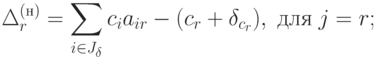 |
( 2.6) |
2) 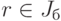 ,
,
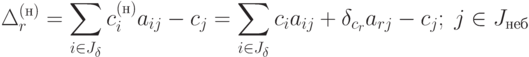 |
( 2.7) |
Очевидно, что для сохранения оптимальности прежнего плана при вариациях
коэффициента cr необходимо и достаточно сохранение
знаков оценок 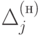 для всех небазисных переменных.
Поэтому из условий
для всех небазисных переменных.
Поэтому из условий 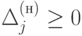 в соответствии с формулами (2.6) и (2.7) можно определить допустимые вариации
коэффициента
в соответствии с формулами (2.6) и (2.7) можно определить допустимые вариации
коэффициента 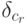 , при которых сохраняется прежнее
оптимальное решение.
, при которых сохраняется прежнее
оптимальное решение.
До сих пор мы рассматривали вариации лишь одного коэффициента целевой функции. Этот же подход можно применить, когда варьируются одновременно несколько коэффициентов ci.
В таком случае получим соотношения, аналогичные (2.7), в которых оценки 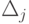 будут функциями уже нескольких параметров
будут функциями уже нескольких параметров 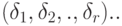 .
.
Решая совместно систему неравенств вида 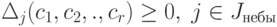 находим условия для вариаций
находим условия для вариаций 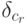 , при которых
прежний оптимальный базис сохраняется.
, при которых
прежний оптимальный базис сохраняется.
Эта задача относится к классу задач параметрического программирования.
3. Варьирование элементов матрицы ограничений A. Рассмотрим лишь случай вариации компонентов небазисных векторов Aj=[aij], i=1,2,...,m, поскольку исследование вариаций компонент базисных векторов Ai довольно сложное, легче заново решить задачу с новыми условиями.
Итак, пусть небазисный вектор Aj=[amj]
изменился. Нужно выяснить, останется ли оптимальным текущий базис. Для
этого полезно применить теорию двойственности. Пусть оптимальный базис
прямой задачи Ax, а соответствующие оптимальные
значения двойственных переменных 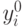 . Как известно, условие
оптимальности
. Как известно, условие
оптимальности 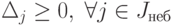 .
Вместе с тем в соответствии с (1.11),
.
Вместе с тем в соответствии с (1.11),  .
Значит, если
.
Значит, если 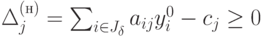 ,
то прежний оптимальный базис сохраняется.
,
то прежний оптимальный базис сохраняется.
4. Добавление еще одного способа производства. Предположим, что первоначально задача имеет вид
 |
( 2.8) |
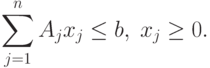 |
( 2.9) |
Предположим, что найден оптимальный базис 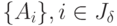 и
соответствующие оптимальные решения прямой
и
соответствующие оптимальные решения прямой 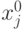 и двойственной
и двойственной 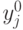 задач.
задач.
Пусть прибавляется еще один (n+1) -й способ производства, которому отвечает вектор технологических затрат An+1=[ai n+1] и коэффициент целевой функции cn+1. Тогда будем иметь следующую задачу:
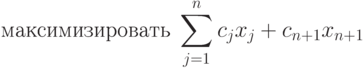 |
( 2.10) |
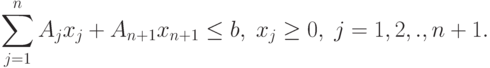 |
( 2.11) |
Нужно определить, изменится ли при этом прежнее оптимальное
решение и при каком значении коэффициента cn+1
выпуск (n+1) -го продукта будет рентабельным
(то есть 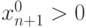 ).
).
Чтобы оптимальное решение после ввода вектора An+1 не изменилось, необходимо, чтобы вектор An+1 и переменная xn+1
оставались небазисными, т.е., чтобы 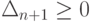 .
На основании теории двойственности получим
.
На основании теории двойственности получим
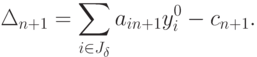
Если 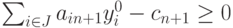 , то прежний
оптимальный план не изменится после включения выпуска (n+1) -го вида продукции.
, то прежний
оптимальный план не изменится после включения выпуска (n+1) -го вида продукции.
Если же 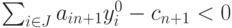 , то выпуск (n+1) -го вида продукции становится рентабельным,
и прежний оптимальный план изменяется.
, то выпуск (n+1) -го вида продукции становится рентабельным,
и прежний оптимальный план изменяется.
