Примеры моделей, получаемых из фундаментальных законов природы
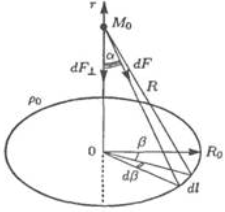
3. Колебания колец Сатурна. Построим модель движения точечной массы М0 в поле сил тяготения, создаваемом материальным кольцом с радиусом R0 линейной плотностью р0. Кольцо считается бесконечно тонким, движение происходит вдоль оси кольца (рис. 2.3).
Данная схема может рассматриваться как идеализация процесса колебаний колец Сатурна. Тем не менее, несмотря на существенные упрощения, непосредственное использование закона всемирного тяготения
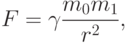
 - постоянная
тяготения, не может дать окончательной модели движения колец
Сатурна, так как массы m0, m1
должны быть точечными.
- постоянная
тяготения, не может дать окончательной модели движения колец
Сатурна, так как массы m0, m1
должны быть точечными.Поэтому вычислим сначала силу притяжения между точечной массой M0 и массой dm, содержащейся в малом элементе кольца dl, которую уже можно считать точечной:
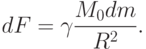
Здесь R, r - соответственно расстояние от
массы М0 до кольца и до центра кольца.
Очевидно, что при 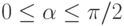 (для
(для  выкладки аналогичны)
выкладки аналогичны)
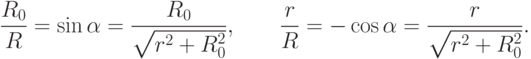
Поскольку


Найдем проекцию силы dF на ось r (именно эта проекция определяет интересующее нас движение):
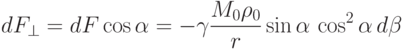
Просуммировав теперь силы тяготения, создаваемые всеми элементами кольца,
т.е. взяв интеграл от  по
по  от
от  до
до 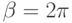 , найдем результирующую силу:
, найдем результирующую силу:
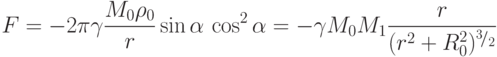 |
( 3) |
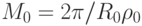 - полная масса кольца.
Как и в предыдущем пункте, горизонтальная проекция результирующей силы
равна нулю из-за симметричного расположения кольца относительно массы М0.
- полная масса кольца.
Как и в предыдущем пункте, горизонтальная проекция результирующей силы
равна нулю из-за симметричного расположения кольца относительно массы М0.Сила тяготения (3) существенно отличается от выражения, даваемого
законом для точечных масс, переходя в него лишь
при 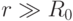 , когда кольцо можно уподобить точечной
массе благодаря большому, в сравнении с размерами кольца, расстоянию
между тяготеющими телами. Если же
, когда кольцо можно уподобить точечной
массе благодаря большому, в сравнении с размерами кольца, расстоянию
между тяготеющими телами. Если же  , то
, то

Применив к массе М0 второй закон Ньютона, получим уравнение ее движения вдоль оси r:
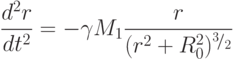
 :
: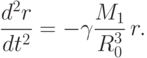 |
( 4) |
4. Заключение.
- Даже в простейших ситуациях для построения модели может потребоваться использование не одного, а нескольких фундаментальных законов.
- Прямое формальное применение фундаментальных законов к объекту, рассматриваемому как целое, не всегда возможно. В этих случаях требуется просуммировать элементарные акты взаимодействия между его частями, принимая во внимание свойства объекта (например, его геометрию).
- Одними и теми же моделями могут описываться совершенно разные по своей природе объекты, подчиняющиеся разным фундаментальным законам, и, наоборот, данному закону могут отвечать принципиально разные модели (например, линейные и нелинейные).
- Необходимо использовать все возможности для проверки правильности построения модели.