Примеры моделей, получаемых из фундаментальных законов природы
2. Отклонение заряженной частицы в электронно-лучевой трубке. Будем считать, что обкладки конденсатора электроннолучевой трубки (рис. 2.2) представляют собой бесконечные плоскости
(предположение справедливо в случае, если расстояние между обкладками много меньше их размеров, а электрон движется на большом удалении от их краев). Очевидно, что электрон будет притягиваться к нижней обкладке и отталкиваться от верхней. Сила притяжения F двух разноименных зарядов элементарно определяется из закона Кулона
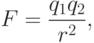
Разобьем всю плоскость нижней обкладки на элементарные "полоски",
характеризующиеся координатами r1, r2, r3 ; 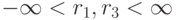 ; r2 = 0 (см. рис. 2.2).
; r2 = 0 (см. рис. 2.2).
Подсчитаем силу притяжения электрона зарядом, находящемся на элементарной площадке ds=dr1dr3 и равным dq=q0ds, где q0 - поверхностная плотность заряда на обкладке. Если частица находится на расстоянии r2 от заряженной плоскости, то
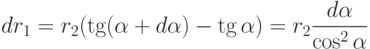
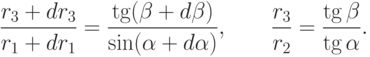
Из последних двух формул находим
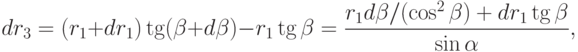
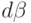 .
Умножая dr1 на dr3
и отбрасывая член более высокого порядка малости,
получаем
.
Умножая dr1 на dr3
и отбрасывая член более высокого порядка малости,
получаем 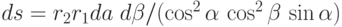 . Сила притяжения электрона с зарядом qе к
элементарной площадке ds равна
. Сила притяжения электрона с зарядом qе к
элементарной площадке ds равна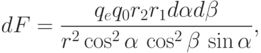
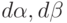 вычисляется по формуле
вычисляется по формуле  . В итоге для
элементарной силы имеем
. В итоге для
элементарной силы имеем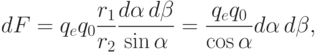
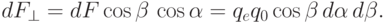
Проинтегрировав выражение для 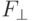 по
по  от
от  до
до 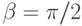 ,
найдем силу притяжения электрона к части элементарной
"полоски", расположенной в квадранте r1 > 0, r3 > 0:
,
найдем силу притяжения электрона к части элементарной
"полоски", расположенной в квадранте r1 > 0, r3 > 0:
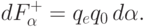
Просуммировав  по
по  от
от 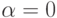 до
до 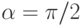 , т.е. по всем
полоскам квадранта r1 > 0, r3 > 0,
определим силу притяжения, индуцируемую зарядами, расположенными
в этом квадранте:
, т.е. по всем
полоскам квадранта r1 > 0, r3 > 0,
определим силу притяжения, индуцируемую зарядами, расположенными
в этом квадранте:
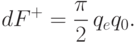
Учитывая действие всех четырех квадрантов плоскости нижней обкладки и проводя аналогичные рассуждения для верхней обкладки, получим результирующую силу притяжения (отталкивания) электрона ко всем зарядам конденсатора
 |
( 2) |
Сила F направлена вдоль оси r2 к нижней обкладке (составляющие F по осям r1, r3, очевидно, равны нулю в силу симметрии - чтобы убедиться в этом, достаточно рассмотреть действие заряда, находящегося на площадке, расположенной в квадранте r1 < 0, r3 < 0 и симметричной площадке ds ).
Поскольку сила F не зависит от r2, а по горизонтальной оси частица движется с постоянной скоростью v, то приходим к ситуации предыдущего пункта - применив второй закон Ньютона, легко получить формулы, аналогичные (1), описывающие движение электрона по параболической траектории и дающие возможность вычислить все ее параметры. Однако в отличие от случая с подлодкой прямое применение фундаментального закона Кулона для получения модели движения электрона оказывается невозможным. Потребовалось, опираясь на фундаментальный закон, сначала описать элементарный акт взаимодействия зарядов, и уж затем, просуммировав все эти акты, удалось найти результирующую силу.
Подобная ситуация и последовательность действий весьма типичны при построении моделей, так как многие фундаментальные законы устанавливают взаимоотношения как раз между элементарными частями исходного объекта. Это, разумеется, справедливо не только для электрических сил, но, например, и для сил тяготения.

