Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели

5. О нелинейности математических моделей. Простота рассмотренных выше моделей во многом связана с их линейностью. В математическом плане это важное понятие означает, что справедлив принцип суперпозиции, т. е. любая линейная комбинация решений (например, их сумма) также является решением задачи. Пользуясь принципом суперпозиции, нетрудно, найдя решение в каком-либо частном случае, построить решение в более общей ситуации. Поэтому о качественных свойствах общего случая можно судить по свойствам частного - различие между двумя решениями носит лишь количественный характер. Например, увеличение в два раза скорости истечения ракетного топлива ведет также к двукратному увеличению скорости ракеты, уменьшение угла падения светового луча на отражающую поверхность означает такое же изменение угла отражения и т.д. Другими словами, в случае линейных моделей отклик объекта на изменение каких-то условий пропорционален величине этого изменения.

Для нелинейных явлений, математические модели которых не подчиняются принципу суперпозиции, знание о поведении части объекта еще не гарантирует знания поведения всего объекта, а его отклик на изменение условий может качественно зависеть от величины этого изменения. Так, уменьшение угла падения луча света на границу раздела двух сред приводит к уменьшению угла преломления, но только до определенного предела. Если угол падения становится меньше критического (см. формулу (9)), то происходит качественное изменение - свет перестает проникать через границу раздела во вторую среду, если она менее плотная, чем первая. Тем самым преломление света - пример нелинейного процесса.

Большинство реальных процессов и соответствующих им математических моделей нелинейны. Линейные же модели отвечают весьма частным случаям и, как правило, служат лишь первым приближением к реальности. Например, популяционные модели сразу становятся нелинейными, если принять во внимание ограниченность доступных популяции ресурсов. При их выводе считается, что:

1) существует "равновесная" численность популяции N_p, которую может обеспечить окружающая среда;

2) скорость изменения численности популяции пропорциональна самой численности, умноженной (в отличие от модели Мальтуса) на величину ее отклонения от равновесного значения, т.е.

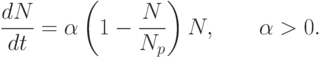( 12)

Член (1 - N/N_p) в этом уравнении обеспечивает механизм "насыщения" численности - при N < N_p (N > N_p) скорость роста положительна (отрицательна) и стремится к нулю, если .

Рис. 1.8.

Представляя уравнение (12) в виде

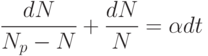
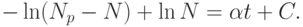
Постоянная интегрирования определяется из условия N(t = 0) = N(0), т.е. 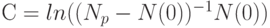. В результате находим

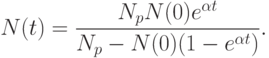
Поведение функции N(t) описывается так называемой логистической кривой (рис. 1.8). При любом N(0) численность стремится к равновесному значению N_p, причем тем медленней, чем величина N(t) ближе к N(0). Тем самым равновесие, в отличие от случая модели (10), устойчиво.

Логистическая модель более реалистично отражает динамику популяции в сравнении с моделью Мальтуса, но сама она с необходимостью становится нелинейной и поэтому более сложной. Заметим, что предположения о механизмах насыщения используются при построении многих моделей в различных областях знаний.

6. Предварительные выводы. Процесс построения моделей может быть условно разбит на следующие этапы.

1. Конструирование модели начинается со словесно-смыслового описания объекта или явления. Помимо сведений общего характера о природе объекта и целях его исследования эта стадия может содержать также некоторые предположения (невесомый стержень, толстый слой вещества, прямолинейное распространение световых лучей и т.д.). Данный этап можно назвать формулировкой предмодели.
2. Следующий этап - завершение идеализации объекта. Отбрасываются все факторы и эффекты, которые представляются не самыми существенными для его поведения. Например, при составлении баланса материи не учитывался, ввиду его малости, дефект масс, которым сопровождается радиоактивный распад. По возможности идеализирующие предположения записываются в математической форме, с тем чтобы их справедливость поддавалась количественному контролю.
3. После выполнения первых двух этапов можно переходить к выбору или формулировке закона ( вариационного принципа, аналогии и т.п.), которому подчиняется объект, и его записи в математической форме. При необходимости используются дополнительные сведения об объекте, также записываемые математически (например, постоянство величины с для всех траекторий лучей света, вытекающее из геометрии задачи). Следует иметь в виду, что даже для простых объектов выбор соответствующего закона отнюдь не тривиальная задача.
4. Завершает формулировку модели ее "оснащение". Например, необходимо задать сведения о начальном состоянии объекта (скорость ракеты и ее массу в момент t = 0 ) или иные его характеристики, без знания которых невозможно определить поведение объекта. И, наконец, формулируется цель исследования модели (найти закон преломления света, достичь понимания закономерностей изменения популяции, определить требования к конструкции ракеты, запускающей спутник, и т. д.).
5. Построенная модель изучается всеми доступными исследователю методами, в том числе со взаимной проверкой различных подходов. В отличие от рассматриваемых простейших случаев, большинство моделей не поддаются чисто теоретическому анализу, и поэтому необходимо широко использовать вычислительные методы. Это обстоятельство особенно важно при изучении нелинейных объектов, так как их качественное поведение заранее, как правило, неизвестно.
6. В результате исследования модели не только достигается поставленная цель, но и должна быть установлена всеми возможными способами (сравнением с практикой, сопоставлением с другими подходами) ее адекватность - соответствие объекту и сформулированным предположениям. Неадекватная модель может дать результат, сколь угодно отличающийся от истинного, и должна быть либо отброшена, либо соответствующим образом модифицирована.