НОУ ИНТУИТ | Введение в математическое программирование. Лекция 1: Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Донецкий национальный технический университет

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать программу

Элементарные математические модели

Рассмотрим некоторые подходы к построению простейших математических моделей, иллюстрирующие применение фундаментальных законов природы, вариационных принципов, аналогий, иерархических цепочек. Несмотря на простоту, привлекаемый материал даст возможность начать обсуждение таких понятий, как адекватность моделей, их "оснащение", нелинейность, численная реализация и ряда других принципиальных вопросов математического моделирования.

1. Фундаментальные законы природы. Наиболее распространенный метод построения моделей состоит в применении фундаментальных законов природы к конкретной ситуации. Эти законы общепризнаны, многократно подтверждены опытом, служат основой множества научно-технических достижений. Поэтому их обоснованность не вызывает сомнений, что, помимо всего прочего, обеспечивает исследователю мощную психологическую поддержку. На первый план выдвигаются вопросы, связанные с тем, какой закон (законы) следует применять в данном случае и как это делать.

а) Сохранение энергии. Этот закон известен почти двести лет и занимает, пожалуй, наиболее почетное место среди великих законов природы. Полагаясь на него, эксперт по баллистике, желающий быстро определить скорость револьверной пули и не имеющий поблизости специальной лаборатории, может воспользоваться относительно простым устройством типа маятника — груза, подвешенного на легком жестком и свободно вращающемся стержне (рис. 1.2).

Рис. 1.2.

Пуля, застрявшая в грузе, сообщит системе "пуля—груз" свою кинетическую энергию, которая в момент наибольшего отклонения стержня от вертикали полностью перейдет в потенциальную энергию системы.

Эти трансформации описываются цепочкой равенств

$\frac{mv^2}{2}=(M+m)\frac{V^2}{2}=(M+m)gl(1-\cos\alpha).$

Здесь mv²/2 — кинетическая энергия пули массы m, имеющей скорость v, M — масса груза, V — скорость системы "пуля—груз" сразу после столкновения, g — ускорение свободного падения, I — длина стержня, $\alpha$ — угол наибольшего отклонения. Искомая скорость определяется формулой

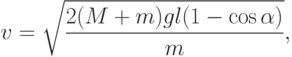$v=\sqrt{\frac{2(M+m)gl(1-\cos\alpha)}{m}},$

( 1)

которая будет вполне точной, если не учитываемые нами потери энергии на разогрев пули и груза, на преодоление сопротивления воздуха, разгон стержня и т. д. невелики. Это, на первый взгляд, разумное рассуждение на самом деле неверно. Процессы, происходящие при "слипании" пули и маятника, уже не являются чисто механическими. Поэтому примененный для вычисления величины V закон сохранения механической энергии несправедлив: сохраняется полная, а не механическая энергия системы. Он дает лишь нижнюю границу для оценки скорости пули (для правильного решения этой простой задачи надо воспользоваться также законом сохранения импульса ).

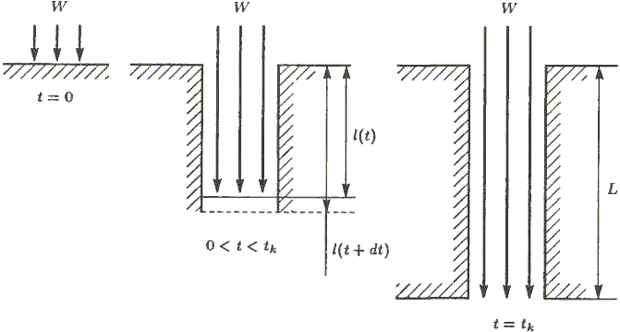
Сходные рассуждения может применить и инженер для оценки времени t_k сверления слоя металла толщины L лазером с мощностью W, излучение которого перпендикулярно поверхности материала (рис. 1.3).

Рис. 1.3. Начальная, промежуточная и конечная стадии сверления металла лазером

Если энергия лазера полностью идет на испарение столбика металла массы 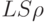$LS \rho$ ( S — облучаемая площадь, LS — объем столбика, $\rho$ — плотность вещества), то закон сохранения энергии выражается равенством

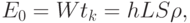$E_0=Wt_k=hLS \rho,$

( 2)

где h — энергия, требуемая для испарения единицы массы. Величина h имеет составную структуру: h=(Т_пл—Т)h₁+h₂+h₃, поскольку материал необходимо последовательно нагреть до температуры плавления Т_пл, а затем расплавить и превратить в пар ( T — исходная температура, h₁ - удельная теплоемкость, h2 и h3, — соответственно удельная теплота плавления и парообразования).

Изменение глубины выемки l(t) со временем определяется из детального баланса энергии в промежутке времени от t до t+dt. На испаренную за это время массу

$[ l(t+dt)-l(t) ] S \rho=dlS \rho$

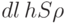тратится энергия $dl\, hS \rho$ , равная энергии 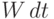$W\,dt$ , сообщаемой веществу лазером: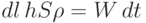

$dl\, hS \rho = W\,dt$

откуда получается дифференциальное уравнение

$\frac{dl}{dt}=\frac{W}{hS \rho}.$

Его интегрирование (с учетом того, что начальная глубина выемки равна нулю) дает

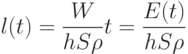$l(t)=\frac{W}{hS\rho}t=\frac{E(t)}{hS\rho}$

( 3)

где E(t) — вся энергия, выделенная лазером к моменту времени t. Следовательно, глубина выемки пропорциональна затраченной энергии (причем величина t_k, когда l(t_k)=L, совпадает с вычисленной по формуле (2)).

В действительности процесс сверления гораздо сложнее рассмотренной схемы - энергия тратится на нагрев вещества, на удаление паров из выемки, которая может иметь неправильную форму, и т.д. Поэтому уверенность в правильности предложенного математического описания значительно меньше, чем в случае с пулей. Вопрос о соответствии объекта и его модели - один из центральных в математическом моделировании, и в дальнейшем мы будем неоднократно к нему возвращаться.

Дальше >>

Авторизоваться

Введение в математическое программирование

Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели

Элементарные математические модели

Вопросы и ответы