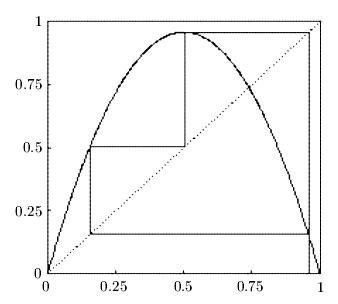
Численное решение нелинейных алгебраических уравнений и систем

При 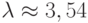цикл P₄ периода 4 становится отталкивающим, 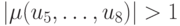; при этом появляются притягивающий цикл периода 8. Дальнейшее увеличение параметра будет приводить к появлению циклов P₁₆, P₃₂ и т.д. Происходит каскад бифуркаций удвоения периода.

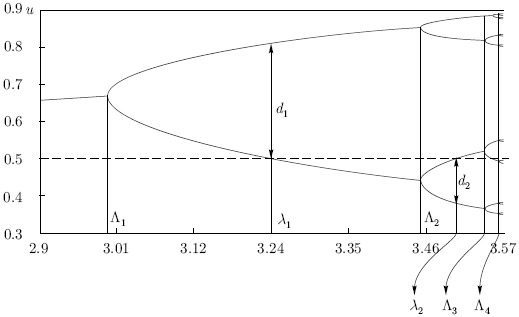
Заметим, что рассмотренный простой процесс имеет сложное поведение. Наблюдается каскад бифуркаций при увеличении величины ; кроме того, все циклы, которые при этом встречаются, имеют период 2^p. Эта важнейшая закономерность, которая прослеживается не только в расчетах, но и в природе! Рассмотренные бифуркации при увеличении можно наглядно представить на бифуркационной диаграмме ( рис. 5.8). Диаграмма получается, если обозначить через 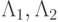те значения 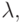в которых происходят бифуркации, а через 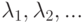при которых u = 0, 5 является элементом циклов P₂, P₄, ...; по вертикальной оси откладываются значения предельных точек отображения. Обозначим за d₁, d₂, ... величины, равные расстоянию между x = 0, 5 и ближайшим к нему элементом цикла P₂ при 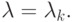Численный эксперимент показал, что 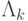и 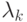при достаточно больших k ведут себя, как геометрическая прогрессия со знаменателем т.е.

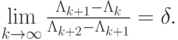
Отношение d_k/d_{k + 1} имеет предел, равный Эти закономерности были замечены американским математиком Фейгенбаумом.

Рис. 5.8.

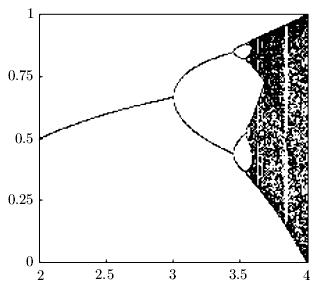
При дальнейшем увеличении последовательность 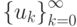приобретает хаотический характер ( 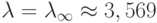), что видно на рис. 5.9.

Рис. 5.9.

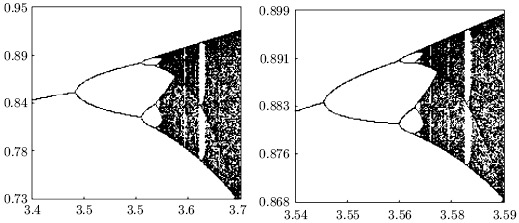
Примечательно, что каскады Фейгенбаума имеют фрактальный характер (т.е. сохраняют подобие при изменении масштабов, рис. 5.10 а, б).

Рис. 5.10.

Изучение графиков функций f²(u) и f¹(u) показывает, что их фрагменты вблизи максимумов близки друг к другу, более того, они отличаются лишь масштабами. Оказывается, что такое же подобие имеет место для функци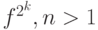и при 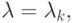и выполняется тем точнее, чем больше n. Если положить u' = u - 1 / 2 (в дальнейшем штрих будем опускать) и считать коэффициентом растяжения вдоль осей, то для некой симметричной функции g(u), определенной на отрезке [- 1, 1], можно получить следующее функциональное уравнение:

которое универсально определяет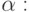

Вблизи максимума g(x) должна быть близка к квадратичной параболе, причем g(0) = 1. В теории универсальности показывается, что эта функция вычисляется с помощью ряда

g(u) = 1 - 1, 52763u2 + 0, 104815u4 - 0, 0267057u6 + ...

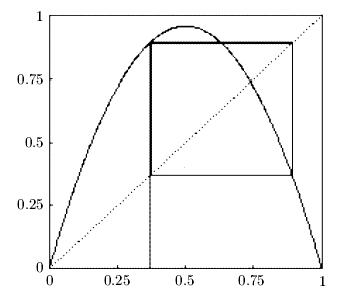
Пусть теперь 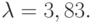В этом случае из хаотической области, изображенной на рис. 5.10, появляется устойчивый цикл P₃ (рис. 5.11 а, b представляют циклы в последовательные моменты времени).

Рис. 5.11a.

Рис. 5.11b.

Циклу на рисунке выше соответствует самое большое окно устойчивых циклов 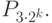Чередование хаотических и регулярных зон — называется перемежаемостью. Возможно, нечто подобное наблюдается в гидродинамических потоках, где ламинарные зоны чередуются с турбулентными.