НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 6: Численное решение нелинейных алгебраических уравнений и систем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

5.3. О вариационных подходах к решению нелинейных систем уравнений

Рассмотрим систему нелинейных уравнений f(u, v) = 0, g(u, v) = 0, ${u, v} \in \Omega.$

Рассмотрим функционал 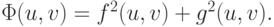$\Phi (u, v) = f^{2}(u, v) + g^{2}(u, v).$

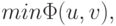Так как $\Phi$ неотрицателен, то найдется точка $\left\{{\bar {u}, \bar {v}}\right\}$ такая, что $\left\{{\bar {u}, \bar {v}}\right\} = \mathop {\arg }\limits_{u, v \in \Omega } \min \Phi (u, v),$ но $min \Phi (u, v),$ очевидно, достигается при f(u, v) = 0, g(u, v) = 0, т.е. на решении исходной системы уравнений.

Построим итерационный процесс, соответствующий методу градиентного спуска

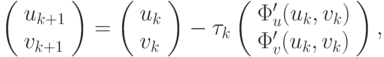
$\left( \begin{array}{l} {u_{k + 1}} \\ {v_{k + 1}} \\ \end{array} \right) = \left( \begin{array}{l} {u_k} \\ {v_k} \\ \end{array} \right) - \tau_k \left( \begin{array}{l} {{\Phi}_u^{\prime}(u_k, v_k)} \\ {{\Phi}_v^{\prime}(u_k, v_k)} \\ \end{array} \right),$

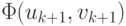где $\tau _{k}$ — параметр, который выбирается, например, из условия минимальности $\Phi (u_{k + 1}, v_{k + 1})$ в данном направлении (метод наискорейшего спуска), {p_k, q_k} — вектор, определяющий направление минимизации. На каждом шаге итераций решается задача минимизации $\Phi$ по одному аргументу.

5.4. Метод Чебышёва построения итерационных процессов высшего порядка

Предположим, что существует функция g(u), обратная к f(u). При этом u = g[f(u)], U = g(0). Пусть, кроме того, f(u) непрерывна и имеет необходимое число непрерывных производных на отрезке, внутри которого лежат все члены последовательности {u_k}, k = 0, 1, ... Обратная функция имеет такое же количество непрерывных производных, как и f(u). Разложим функцию g(f[v]) = g(h) в ряд Тейлора в окрестности корня - точки w = f(u)

${g(h)} \approx g(w) + \sum\limits_{i = 1}^{n}{\frac{g^{(i)}(w)}{{i}!} (h - w)^{i}.$

Тогда, учитывая, что u = g[f(u)], w = f(u), h = f(v), получим

$g(0) = U \approx u + \sum\limits_{i = 1}^{n}{\frac{{g^{i}[f(u)]}}{{i!}}} [- f(u)]^{i} + \ldots.$

Можно показать, что итерационный метод

$u_{k + 1} = u_k + \sum\limits_{i = 1}^{n}(- 1)^{i} \frac{g^{(i)} \left[{f(u_k)}\right]}{i!}[f(u_k)]} ^{i}, u^0 = a$

имеет порядок сходимости n + 1. Для вычисления производных обратной функции u = g[f(u)] воспользуемся правилом дифференцирования сложной функции:

$\begin{gather*} 1 = g^{(1)} [f(u)] \cdot f^{(1)} (u), \\ 0 = g^{(2)} [f(u)] \cdot [f^{(1)} (u)]^2 + g^{(1)} [f(u)]\cdot f_{(u)}^{(2)}, \\ 0 = g^{(3)} [f(u)] \cdot [f_{(u)}^{(1)} ]^3 + 3g^{(2)} [f(u)]\cdot f_{(u)}^{(2)} \cdot f_{(u)}^{(1)} + g^{(1)} [f(u)]\cdot f_{(u)}^{(3)}, \\ \ldots \end{gather*}$

5.5. Разностные отображения в нелинейной динамике

Рассмотрим последовательность чисел $u_{k + 1} \in R$ ( R — множество вещественных чисел), каждый член которой связан с предыдущим рекуррентным соотношением

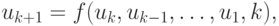$u_{{k + 1}} = f(u_k, u_{{k - 1}}, \ldots , u_{1}, k),$

( 5.4)

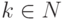где $k \in N$ ( N — множество натуральных чисел). Соотношения (5.4) называются разностными отображениями (уравнениями) с дискретным аргументом.

Такие уравнения появляются при моделировании процессов, в которых величина u рассматривается через определенные промежутки времени. Например, еще в середине XIX века Ферхюльст для описания динамики популяционной системы предложил измерять ежегодно численность особей u_k, где k — номер года. Относительная численность u_{k + 1} полагалась пропорциональной численности в k год, однако она начинает убывать, когда животных становится много ( u_k сравнимо с 1):

$u_{k + 1} = f(u_k),$

( 5.5)

где

$f(u_k) = \lambda u_k(1 - u_k), u_0 = a.$

( 5.6)

Другой пример из экономической области — задача о банковских сбережениях. Пусть u₀ — денежный вклад, растущий в соответствии с постоянным процентом 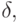$\delta,$ по закону:

$u_{k + 1} = (1 + \delta )u_k = \ldots = (1 + \delta )^{k}u_0.$

Пусть далее законодательный орган, желая воспрепятствовать такому обогащению вкладчика, издает закон о том, чтобы процент убывал пропорционально u_k, т.е.

$\delta_k = \delta_0 \left({1 - \frac{u_k}{u_{\max }}}\right).$

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численное решение нелинейных алгебраических уравнений и систем

5.3. О вариационных подходах к решению нелинейных систем уравнений

5.4. Метод Чебышёва построения итерационных процессов высшего порядка

5.5. Разностные отображения в нелинейной динамике

Вопросы и ответы