Выполнение аналога демоЕГЭ-2007

В2. Найти число решений уравнения (число различных комбинаций значений логических переменных), сами значения можно не находить:

.

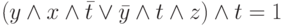Решение. Выражение представляет произведение двух условий, поэтому будет равно 1 ("истине") тогда и только тогда, когда оба множителя равны 1. Следовательно, t = 1 и выражение в скобках должно быть равно 1. Так как выражение в скобках представляет собой сумму двух слагаемых, то для его равенства 1 необходимо, чтобы хотя бы одно из слагаемых было равно 1. Первое слагаемое равно 0 при любом значении x, так как t = 1. Второе слагаемое равно 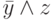и может равняться 1 лишь тогда, когда y = 0 и z = 1. Итак, будет всего два различных решения уравнения, а именно, (x, y, z, t) = (0, 0, 1, 1), (1, 0, 1, 1). Замечание: можно было бы найти количество всех комбинаций переменных, равное 16 и отнять от него число решений уравнения с правой частью равной нулю (сравните эти два подхода по сложности).

Ответ: 2.