НОУ ИНТУИТ | Единый государственный экзамен по информатике. Лекция 2: Минимум теоретических сведений по школьной информатике

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 04.06.2007 | Уровень: для всех | Доступ: свободно | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать программу

Аннотация: Даются основные определения, необходимые для сдачи ЕГЭ по информатике

Ключевые слова: информатика, информация, мера информации, состояние системы, мера, код, кодирование, декодирование, открытое сообщение, закрытое сообщение, шифрование, система счисления, ПО, основание, сложение, единица, таблица, обратный код числа, высказывание, истина, ложь, true, логическая переменная, алгебра предикатов, операции, алгоритм, базовые алгоритмические структуры, ветвление, тело цикла, команда цикла, данные, одномерный массив, двумерный массив, исполнитель, автомат, компьютер, ввод, вывод, АЛУ, УУ, ОЗУ, оперативное запоминающее устройство, hardware, software, персональный компьютер, ядро персонального компьютера, интерфейсная система, операционная система, файловая система, файл, запись, машинный язык, программа, память, работ, транслятор, модель, новая информационная технология, база данных, БД, СУБД, запрос, поиск, сортировка, язык запросов к базе данных, электронная почта, обратное преобразование, телеконференция, базовая, автоматизированная система, человеко-машинная система, автоматизированное рабочее место, компьютерный офис, Технология Рабочая группа, технология клиент-сервер, сервер, процессор, доступ, технологии использования интегрированных пакетов прикладных программ, ППП, связь, предметной области, интерфейс, технологии машинной графики и визуализации, гипертекст, место, пользователь, мультимедиа, multimedia, гипермедиа, hypermedia, мультимедийность, Средства гипермедиа

Минимум теоретических сведений по школьной информатике

Информатика - это междисциплинарная, методологическая наука об информационных процессах, о моделях, об алгоритмах и алгоритмизации, о программах и программировании, об исполнителях алгоритмов и различных исполняющих системах, об их использовании в обществе, в природе, в познании.

Информация - это некоторая упорядоченная последовательность сообщений, отражающих, передающих, увеличивающих наши знания.

Приведём основные соотношения между единицами измерения сообщений:

1 бит (binary digit - двоичная единица) = 0 или 1,

1 байт = 8 битов,

1 килобайт (1Кб) = 2¹³ бит,

1 мегабайт (1Мб) = 2²³ бит,

1 гигабайт (1Гб) = 2³³ бит,

Мера информации - критерий оценки количества информации, разнообразия и определенности в информационной системе.

Пусть известны N состояний системы S ( N опытов с различными, равновозможными, последовательными состояниями системы). Если каждое состояние системы закодировать двоичными кодами, то мера разнообразия состояний системы (мера количества информации) задаётся формулой Р. Хартли:

H=log₂N (бит).

Код - правило соответствия набора знаков одного множества Х знакам другого множества Y . Если каждому символу Х при кодировании соответствует отдельный знак Y, то это кодирование . Если для каждого символа из Y найдется по некоторому правилу однозначно его прообраз в X, то это правило называется декодированием .

При представлении сообщений в ЭВМ все символы кодируются байтами.

Сообщение, которое мы хотим передать адресату, назовём открытым сообщением .

Зашифрованное сообщение может быть построено над другим алфавитом. Назовём его закрытым сообщением.

Процесс преобразования открытого сообщения в закрытое сообщение и есть шифрование .

Любая система счисления - это система кодирования числовых величин (количеств), позволяющая выполнять операции кодирования и декодирования, то есть по любой количественной величине однозначно находить его кодовое представление и по любой кодовой записи - восстанавливать соответствующую ей числовую величину.

Все системы счисления строятся по общему принципу: определяется величина р - основание системы, а любое число х записывается в виде комбинации степеней веса р от 0 -ой до n -ой степени следующим образом:

(x)₁₀=x_npⁿ+x_n-1p^n-1+...+x₁p¹+x₀p⁰.

Сложение в двоичной системе счисления осуществляется по правилам:

0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 2₁₀ = 10₂ (единица идет в старший разряд).

Таблица вычитания в двоичной системе счисления имеет вид:

0 - 0 = 0, 1 - 0 = 1, 1 - 1 = 0, 0 - 1 = 10 - 1 = 1 (единицу забираем у старшего разряда).

Таблица умножения в двоичной системе счисления имеет вид:

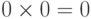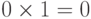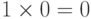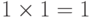$0 \times 0 = 0$ , $0 \times 1 = 0$ , $1 \times 0 = 0$ , $1 \times 1 = 1$ .

Таблица деления в двоичной системе счисления имеет вид:

0 : 0 = не определено, 1 : 0 = не определено, 0 : 1 = 0, 1 : 1 = 1.

Обратным кодом числа в системе с основанием р называется число в этой системе, получаемое заменой цифры, символа в каждом разряде числа на его дополнение до максимальной цифры в системе (то есть до р-1 ).

Дополнительный код = обратный код + единица в младшем разряде.

Высказывание - некоторое повествовательное утверждение, про которое можно однозначно сказать ("сразу посмотрев на него"), истинно оно или ложно. Эти два значения всевозможных высказываний обозначаются "истина" и "ложь", "true" и "fаlse" или "1" и "0".

Переменная, значениями которой могут быть лишь значения "1" или "0" называется логической переменной или булевой переменной.

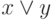Множество логических переменных $x, y\in X$ с определенными над ним операциями: x - отрицания или инверсии, $x\vee y$ - логического сложения или дизъюнкции, 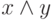$x\wedge y$ - логического умножения или конъюнкции называется алгеброй предикатов (и высказываний), если эти операции удовлетворяют следующим аксиомам:

Аксиома двойного отрицания:
$\bar\bar x = x$ .
Аксиомы переместительности операндов:
$x \wedge y=y \wedge x$ , $x \vee y=y \vee x$ .
Аксиомы переместительности операций дизъюнкции и конъюнкции:
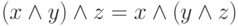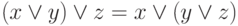$(x \wedge y) \wedge z=x \wedge (y \wedge z)$ , $(x \vee y) \vee z=x \vee (y \vee z)$ .
Аксиомы одинаковых операндов:
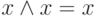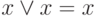$x \wedge x=x$ , $x \vee x=x$ .
Аксиомы поглощения:
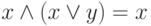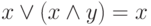$x \wedge (x \vee y)=x$ , $x \vee (x \wedge y)=x$ .
Аксиомы распределения операции:
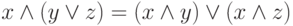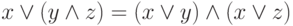$x \wedge (y \vee z)=(x \wedge y) \vee (x \wedge z)$ , $x \vee (y \wedge z)=(x \vee y) \wedge (x \vee z)$ .
Аксиомы де Моргана:
$x \wedge y=\bar x \vee \bar y$ , $x \vee y= \bar x \wedge \bar y$ .
Аксиомы нейтральности:
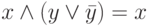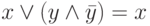$x \wedge (y \vee \bar y)=x$ , $x \vee (y \wedge \bar y)=x$ .
Аксиома существования единицы ( истина, true, 1 ) и нуля ( ложь, false, 0 ), причем:
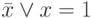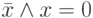$\bar x \vee x=1$ , $\bar x \wedge x=0$ .

Из этих аксиом следует ряд полезных соотношений, например,

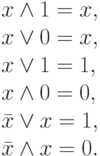
$x \wedge 1=x,\\ x \vee 0=x,\\ x \vee 1=1,\\ x \wedge 0=0,\\ \bar x \vee x=1,\\ \bar x \wedge x=0.$

Три базовые операции определяются таблицей их значений, так как из-за дискретности значений логических переменных, часто используется табличная форма задания.

Итак, эти операции определяются совмещенной таблицей значений вида:

x	y	x	$x \wedge y$	$x \vee y$
0	0	1	0	0
0	1	1	0	1
1	0	0	0	1
1	1	0	1	1

Такая таблица всех значений некоторой логической функции называется таблицей истинности этой функции.

Дальше >>

Авторизоваться

Единый государственный экзамен по информатике

Минимум теоретических сведений по школьной информатике

Минимум теоретических сведений по школьной информатике

Вопросы и ответы