Проект "Выпуклая оболочка"

Реализация класса Polygon

Нам осталось реализовать методы perimeter, area и add класса Polygon. Как это уже отмечалось при уточнении постановки задачи, вся работа по модификации выпуклой оболочки и перевычислению ее площади и периметра должна проводиться при добавлении новой точки, а действие методов perimeter и area будет сводиться просто к выдаче уже вычисленных ранее значений, хранящихся в private -компонентах.

class Polygon extends Deq implements Figure {
        private double s, p;
        public double perimeter() {
            return p;
        }
        public double area() {
            return s;
        }
        ...
    }

Для того чтобы реализовать метод add и конструктор класса Polygon, необходимо аккуратно разобраться с тем, как именно вершины выпуклой оболочки хранятся в деке. Определение 2.3 освещенности, данное выше, предполагает, что все вершины оболочки расположены в деке последовательно, одна за другой. При этом важен порядок обхода — против часовой стрелки, называемый также ориентацией.

Это должно учитываться в конструкторе, который создает простейший из многоугольников, — треугольник, размещая заданные ему вершины в деке в нужном порядке. Кроме этого конструктор обязан вычислять периметр и площадь получившегося треугольника, причем площадь должна быть неориентированной, что достигается с помощью метода Math.abs, находящего абсолютное значение своего аргумента.

public Polygon(R2Point a, R2Point b, R2Point c) {
        pushFront(b);
        if (b.light(a, c)) {
            pushFront(a); pushBack(c);
        } else {
            pushFront(c); pushBack(a);
        }
        p = R2Point.dist(a, b) + R2Point.dist(b, c)
            + R2Point.dist(c, a);
        s = Math.abs(R2Point.area(a, b, c));
    }

Назовем ребро 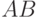(см. рис. рис. 11.6), соединяющее конец дека с его началом, текущим. Так как в деке в каждый момент времени доступны только два элемента — начало и конец, то и работать можно только с текущем ребром многоугольника. Текущее ребро многоугольника, впрочем, легко сменить: если переместить один элемент из начала дека в конец, то многоугольник не изменится, а текущем ребром станет ребро (следующее за 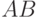в порядке против часовой стрелки). Если переместить из начала дека в конец еще один элемент, то текущим станет ребро 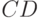и т.д.

Рис. 11.6. Добавление новой точки

При добавлении новой точки возможны два случая. Если в многоугольнике освещенных ребер нет, то это означает, что новая точка попала внутрь или на границу старой выпуклой оболочки, и, следовательно, делать ничего не надо. Если же освещенные ребра есть, то их надо удалить и соединить концы оставшейся ломаной с новой точкой.

При реализации метода add в этом случае необходимо для всех освещенных ребер выпуклой оболочки выполнить следующие действия: удалить это ребро, уменьшить периметр оболочки на его длину и увеличить площадь оболочки на величину, равную площади треугольника, образованного удаляемым ребром и добавляемой точкой. После этого необходимо добавить к оболочке два новых ребра, а к ее периметру — сумму их длин (см. рис. рис. 11.6).

Пересчет периметра и площади, который необходимо производить для каждого из удаляемых ребер, выделен из соображений оптимизации в отдельный private -метод grow.

private void grow(R2Point a, R2Point b, R2Point t) {
        p -= R2Point.dist(a, b);
        s += Math.abs(R2Point.area(a, b, t));
    }

Полный текст построенной программы приведен ниже, в последней секции текущего параграфа.