Индуктивные функции на пространстве последовательностей
В первом параграфе данной главы мы уже познакомились с индуктивными функциями и даже рассмотрели простейшую программу, написанную с помощью применения схемы вычисления индуктивной функции — программу вычисления значения многочлена (см. решение задачи 7.6 "Базисные схемы обработки информации" ). К сожалению, подавляющее большинство функций на пространстве последовательностей индуктивными не являются, что требует дальнейшего развития теории.
Весьма подробное рассмотрение вопросов, связанных с индуктивными функциями, и большое число задач на их применение содержатся в книге [9].
Критерий индуктивности и стационарные значения
Напомним основное определение.
Функция 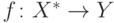 называется индуктивной,
если
называется индуктивной,
если  можно вычислить, зная
можно вычислить, зная 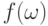 и
и  , т.е. если
, т.е. если  такое, что
такое, что  .
.
Доказательство индуктивности функции обычно проводят конструктивно, предъявляя требуемую функцию  . Именно она
позволяет
написать программу, реализующую схему вычисления индуктивной функции.
Для доказательства же того факта, что заданная функция не является
индуктивной,
применяют следующий критерий индуктивности (точнее его отрицание ).
. Именно она
позволяет
написать программу, реализующую схему вычисления индуктивной функции.
Для доказательства же того факта, что заданная функция не является
индуктивной,
применяют следующий критерий индуктивности (точнее его отрицание ).
Теорема 9.1. Критерий индуктивности. 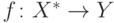 индуктивна
индуктивна 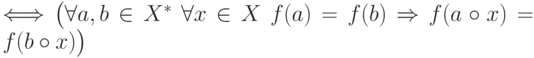 .
.
Теорема утверждает, что  индуктивна тогда и только тогда,
когда из равенства значений
индуктивна тогда и только тогда,
когда из равенства значений  на последовательностях
на последовательностях  и
и  следует
равенство значений
следует
равенство значений  на любых одинаково удлиненных
последовательностях
на любых одинаково удлиненных
последовательностях  и
и  .
.
Доказательство
Необходимость сформулированного в критерии условия немедленно следует из
определения индуктивности. Если  — индуктивна, то
— индуктивна, то 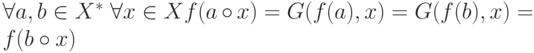 .
.
Для доказательства достаточности построим требуемое отображение  такое, что
такое, что 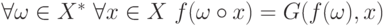 . Зададим это отображение формулой
. Зададим это отображение формулой

Корректность этого определения вытекает из заданного в условии теоремы
свойства функции  . В самом деле, пусть найдутся две различные
цепочки
. В самом деле, пусть найдутся две различные
цепочки  и
и  такие, что
такие, что  . Тогда
можно гарантировать, что
. Тогда
можно гарантировать, что 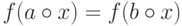 , что и доказывает корректность
определения
отображения
, что и доказывает корректность
определения
отображения  , ибо
, ибо  действительно не зависит
от выбора конкретного
прообраза элемента
действительно не зависит
от выбора конкретного
прообраза элемента  .
.
Так как 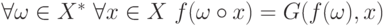 для построенного отображения
для построенного отображения  , то
теорема полностью
доказана.
, то
теорема полностью
доказана.
В качестве примера использования критерия индуктивности
докажем, что функция 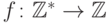 количество максимальных элементов последовательности целых чисел не
является индуктивной. Возьмем
количество максимальных элементов последовательности целых чисел не
является индуктивной. Возьмем 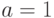 ,
, 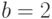 ,
, 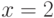 . Тогда
. Тогда  ,
но
,
но 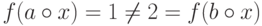 .
.
Схема вычисления индуктивной функции, приведенная в "Базисные схемы обработки информации" , может быть несколько упрощена при условии наличия у функции так называемых стационарных значений.
Определение 9.1.
Значение  индуктивной функции
индуктивной функции 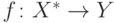 называется стационарным, если
называется стационарным, если  .
.
Так, например, для функции 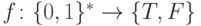 все элементы цепочки равны нулю значение
все элементы цепочки равны нулю значение  является
стационарным.
является
стационарным.
В том случае, если индуктивная функция определена только на  для
для  ,
ее вычисление может начинаться не с пустой, a с одноэлементной или даже более
длинной цепочки. Это, однако, приводит к более сложной программе, чего
можно иногда избежать, доопределяя исходную функцию.
,
ее вычисление может начинаться не с пустой, a с одноэлементной или даже более
длинной цепочки. Это, однако, приводит к более сложной программе, чего
можно иногда избежать, доопределяя исходную функцию.
Индуктивную функцию  произведение элементов числовой последовательности можно доопределить с
сохранением функции
произведение элементов числовой последовательности можно доопределить с
сохранением функции  следующим образом:
следующим образом: 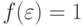 .
.
Для того чтобы расширить сферу применимости схемы вычисления индуктивной функции вводится понятие индуктивного расширения.
Индуктивные расширения
Определение 9.2.
Функция 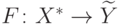 называется индуктивным
расширением функции
называется индуктивным
расширением функции 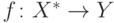 , если
, если
1)  индуктивна,
индуктивна,
2) 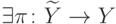 такое, что
такое, что 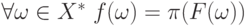 .
.
Рассмотрим функцию 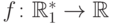 среднее арифметическое элементов последовательности,
которая не является индуктивной. Тогда функция
среднее арифметическое элементов последовательности,
которая не является индуктивной. Тогда функция  ,
определенная
по формуле
,
определенная
по формуле  , где
, где  ,
, 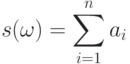 , а
, а  ,
является индуктивным расширением исходной функции
,
является индуктивным расширением исходной функции  , и
, и 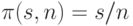 .
.
Для вычисления значения 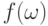 не являющейся индуктивной
функции
не являющейся индуктивной
функции  на цепочке
на цепочке  применяется следующая обобщенная схема.
применяется следующая обобщенная схема.
Обобщенная схема вычисления индуктивной функции. Строится индуктивное расширение  исходной функции, которое
позволяет
ценой увеличения запоминаемой
информации о цепочке
исходной функции, которое
позволяет
ценой увеличения запоминаемой
информации о цепочке  (в
(в 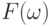 информации
больше,
чем в
информации
больше,
чем в 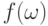 ) применить схему вычисления индуктивной
функции к
) применить схему вычисления индуктивной
функции к 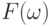 , а затем просто найти
, а затем просто найти 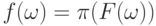 .
.
Пусть 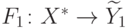 и
и 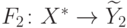 — два индуктивных расширения функции
— два индуктивных расширения функции 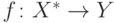 .
Будем говорить, что
.
Будем говорить, что  , если
, если 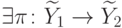 такое, что
такое, что  .
.
Определение 9.3. Минимальным индуктивным расширением функции 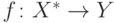 называется индуктивное расширение
называется индуктивное расширение 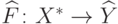 такое, что
такое, что
1) 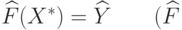 —
сюръективно);
—
сюръективно);
2) для любого индуктивного расширения  функции
функции  выполнено
выполнено
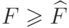 .
.
Минимальные индуктивные расширения хороши тем, что уменьшают количество дополнительной информации, которая должна быть запомнена на каждом шаге для обеспечения возможности перевычисления функции на удлиненной цепочке.
Для любой функции на пространстве последовательностей существует и единственно (в определенном смысле), ее минимальное индуктивное расширение. Доказательство этого факта проведем в два этапа, сначала убедившись в единственности расширения.
Теорема 9.2.
Минимальное индуктивное расширение любой функции 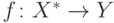 единственно с точностью до изоморфизма.
единственно с точностью до изоморфизма.
Доказательство
Пусть для функции 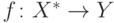 существуют два
минимальных индуктивных расширения
существуют два
минимальных индуктивных расширения 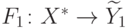 и
и 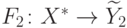 . Тогда в силу их
минимальности имеем
. Тогда в силу их
минимальности имеем 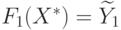 и
и  .
.
Так как  (ибо
(ибо 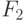 —
минимально), то
—
минимально), то 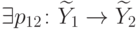 такое, что
такое, что 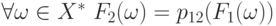 . С
другой стороны,
. С
другой стороны,  и
и 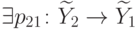 такое, что
такое, что 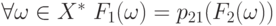 .
Для доказательства теоремы нужно показать, что отображения
.
Для доказательства теоремы нужно показать, что отображения 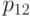 и
и  биективны. Рассмотрим композиции этих отображений
биективны. Рассмотрим композиции этих отображений  и
и  и докажем,
что они являются
тождественными отображениями множеств
и докажем,
что они являются
тождественными отображениями множеств  и
и  соответственно (из этого и следует биективность
отображений
соответственно (из этого и следует биективность
отображений 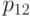 и
и  ).
).
Возьмем произвольный элемент  . Из
сюръективности
. Из
сюръективности 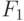 следует, что найдется цепочка
следует, что найдется цепочка 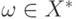 ,
такая что
,
такая что  и поэтому
и поэтому  .
Полученное равенство показывает, что
.
Полученное равенство показывает, что 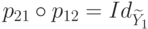 — тождественное отображение.
Рассматривая произвольный элемент
— тождественное отображение.
Рассматривая произвольный элемент  , аналогично
получаем, что
, аналогично
получаем, что  , что и
завершает
доказательство теоремы.
, что и
завершает
доказательство теоремы.
