Индуктивные функции на пространстве последовательностей
Применение теории индуктивных функций
В качестве первого примера рассмотрим уже встречавшуюся нам ранее задачу.
Задача 9.1. Напишите программу, вводящую последовательность целых чисел, и печатающую количество ее максимальных элементов.
Решение В данной задаче 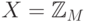 ,
,  ,
, 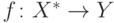 .
Взяв
.
Взяв 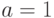 ,
, 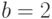 ,
, 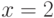 ,
находим
,
находим  , но
, но  .
Из отрицания критерия индуктивности заключаем, что
.
Из отрицания критерия индуктивности заключаем, что  не является
индуктивной.
не является
индуктивной.
Для построения ее индуктивного расширения  применим
стандартный прием.
Попробуем выразить значение функции
применим
стандартный прием.
Попробуем выразить значение функции  на удлиненной
цепочке через ее значение
на удлиненной
цепочке через ее значение 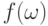 на исходной и элемент
на исходной и элемент  . Известно,
что это невозможно сделать (
. Известно,
что это невозможно сделать (  — не является индуктивной),
но наша цель — понять
какой именно информации не хватает и, добавив ее, образовать функцию
— не является индуктивной),
но наша цель — понять
какой именно информации не хватает и, добавив ее, образовать функцию 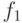 .
Рассмотрим теперь функцию
.
Рассмотрим теперь функцию  . В том случае, если она
индуктивна,
требуемое расширение построено. Иначе повторим предыдущие действия и
попытаемся выразить
. В том случае, если она
индуктивна,
требуемое расширение построено. Иначе повторим предыдущие действия и
попытаемся выразить  и
и 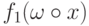 через
через 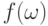 ,
,  и
и  с
использованием дополнительной информации
с
использованием дополнительной информации  . Получаем следующего кандидата на роль индуктивного
расширения
— функцию
. Получаем следующего кандидата на роль индуктивного
расширения
— функцию 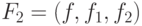 . При необходимости данный процесс
может быть
продолжен и далее, а его завершение гарантируется теоремой о существовании
индуктивного расширения. В данном случае имеем
. При необходимости данный процесс
может быть
продолжен и далее, а его завершение гарантируется теоремой о существовании
индуктивного расширения. В данном случае имеем 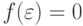 ,
,

Мы видим, что в качестве 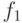 следует взять функцию
следует взять функцию 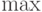 , вычисляющую
максимальное значение элементов цепочки. Тогда для
, вычисляющую
максимальное значение элементов цепочки. Тогда для  получаем
получаем

Эта функция, однако, не определена
на пустой цепочке, поэтому  также определена только на
также определена только на 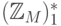 . Воспользовавшись тем, что диапазон
представления
целых чисел на ЭВМ ограничен, в данном случае можно доопределить
. Воспользовавшись тем, что диапазон
представления
целых чисел на ЭВМ ограничен, в данном случае можно доопределить  с сохранением функции перевычисления следующим образом:
с сохранением функции перевычисления следующим образом:  "Integer.MIN\_VALUE" (
"Integer.MIN\_VALUE" (  для языка Java).
Действительно,
если принять, что максимальным
элементом пустой цепочки является минимально представимое на ЭВМ целое число,
то
для языка Java).
Действительно,
если принять, что максимальным
элементом пустой цепочки является минимально представимое на ЭВМ целое число,
то  , а функция
, а функция  определяется формулой
определяется формулой

Докажем, что построенное нами расширение  не является
минимальным.
Для этого достаточно предъявить значение
не является
минимальным.
Для этого достаточно предъявить значение  , которое не принимается ни на одной цепочке. Таковым будет,
например,
, которое не принимается ни на одной цепочке. Таковым будет,
например, 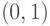 . Докажите самостоятельно, что если вместо
пространства
. Докажите самостоятельно, что если вместо
пространства  рассмотреть
рассмотреть  , то построенное нами
расширение окажется минимальным.
, то построенное нами
расширение окажется минимальным.
Теперь можно написать программу, реализующую построенный алгоритм.
Текст программы
public class NumMaxSeq2 {
public static void main(String[] args) {
int y1 = 0, y2 = Integer.MIN_VALUE;
try {
while (true) {
int x = Xterm.inputInt("x -> ");
if (x == y2) {
y1 += 1;
} else if(x > y2) {
y1 = 1;
y2 = x;
}
}
} catch (Exception e) {
Xterm.println("\nn = " + y1);
}
}
}Любая ошибка при вводе рассматривается здесь, как
завершение последовательности чисел.
Имена переменных, имеющихся в программе, совпадают с использованными при
построении алгоритма, вычисление  выполняется с
помощью
команд "int y1=0, y2=Integer.MIN\_VALUE;", функция
выполняется с
помощью
команд "int y1=0, y2=Integer.MIN\_VALUE;", функция  реализована при
помощи оператора if-else, в котором опущен случай
реализована при
помощи оператора if-else, в котором опущен случай  (так как тогда не
нужно изменять ни
(так как тогда не
нужно изменять ни 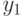 , ни
, ни 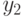 ), а применение
отображения
), а применение
отображения  сводится
к печати только значения
сводится
к печати только значения 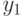 из вычисленных
из вычисленных 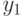 и
и 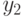 .
.
Следующая задача нам тоже уже знакома.
Задача 9.2. Напишите программу, определяющую номер  первого элемента, равного
первого элемента, равного  , в
последовательности целых чисел. В том случае, если число
, в
последовательности целых чисел. В том случае, если число  в
последовательности не встречается, положите
в
последовательности не встречается, положите  равным нулю.
равным нулю.
Решение
Имеем 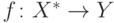 , где
, где 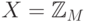 ,
а
,
а  .
Если
.
Если 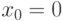 ,
,  ,
,  , то
, то 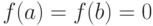 , но
, но  , следовательно
, следовательно  не является индуктивной.
не является индуктивной.
Построим ее индуктивное расширение  . Заметим, что
. Заметим, что  ,
,
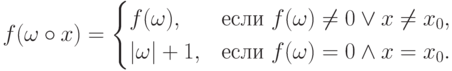
Следовательно, в качестве 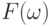 можно взять пару
можно взять пару  ,
где функция
,
где функция  .
Эта функция уже индуктивна, так как
.
Эта функция уже индуктивна, так как 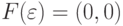 , а
преобразование
, а
преобразование  имеет вид
имеет вид
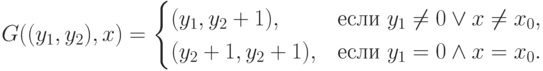
Заметим, что все значения функции  , отличные от нуля, являются
стационарными, в то время как функция
, отличные от нуля, являются
стационарными, в то время как функция  не имеет стационарных
значений.
Ясно, что отображение
не имеет стационарных
значений.
Ясно, что отображение  имеет вид
имеет вид  .
.
Построенное нами расширение не является минимальным, так как значение 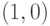 не может быть принято функцией
не может быть принято функцией  ни на одной
цепочке.
ни на одной
цепочке.
Вот программа, не использующая наличия стационарных значений.
Текст программы
public class First1{
public static void main(String[] args) throws Exception {
int x0 = Xterm.inputInt("x0 ->");
int y1 = 0, y2 = 0;
try {
while (true) {
int x = Xterm.inputInt("x -> ");
y2 += 1;
if ( (y1 == 0) && (x == x0) )
y1 = y2;
}
} catch (Exception e) {
Xterm.println("\nn = " + y1);
}
}
}Имена программных переменных совпадают с использованными при
построении алгоритма, вычисление  выполняется с
помощью
команд "int y1=0, y2=0;", реализация функции
выполняется с
помощью
команд "int y1=0, y2=0;", реализация функции  очевидна,
а применение отображения
очевидна,
а применение отображения  сводится
к печати только значения
сводится
к печати только значения 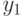 .
.
Программа, использующая наличие у функции  стационарных
значений,
может выдавать ответ сразу же, как только одно из таких значений будет
достигнуто.
стационарных
значений,
может выдавать ответ сразу же, как только одно из таких значений будет
достигнуто.
Текст программы
public class First2 {
public static void main(String[] args) throws Exception {
int x0 = Xterm.inputInt("x0 -> ");
int y1 = 0, y2 = 0;
try {
while (y1 == 0) {
int x = Xterm.inputInt("x -> ");
y2 += 1;
if (x == x0)
y1 = y2;
}
} catch(Exception e){
System.exit(0);
}
Xterm.println("\nn = " + y1);
}
}По достижению конца вводимой последовательности эта программа не выполняет
никаких специальных действий (оператор ";" в блоке "catch" ).
В этой ситуации, как и в случае принятия функцией  любого из
стационарных
значений (
любого из
стационарных
значений (  ), управление просто передается на оператор
печати.
), управление просто передается на оператор
печати.

 тривиально:
тривиально: