Проектирование цикла при помощи инварианта

Теория воздушного шарика

До сих пор мы использовали для построения программ готовые, не ясно откуда взявшиеся инварианты. На практике, конечно, постановка задачи не включает в себя инвариант. Однако любая корректная постановка задачи содержит ее пред- и постусловия: , поэтому они и должны послужить основой для построения инварианта.

Теперь нужно понять, какой именно из двух предикатов и более важен для построения инварианта. Приведем два аргумента в пользу постусловия .

Первый таков: предусловие достаточно часто имеет вид , что соответствует отсутствию ограничений на начальные условия, в которых должна правильно работать программа. Понятно, что в этом случае инвариант можно строить только исходя из постусловия .

Второй аргумент: представим себе в виде цели, которой должен достичь путник на местности, а в виде точки его начального расположения. Инвариант, который мы хотим построить, должен помочь путнику достичь нужной ему цели. Можно ли надеяться на это, полностью проигнорировав ?

Если не помнить постоянно о цели в процессе написания программы, то весьма маловероятно, что она все же окажется достигнутой. Из какой бы начальной точки путник не вышел, если у него нет цели, он до нее не доберется!

Именно по этой причине программирование называют целенаправленной деятельностью, а за основу для построения инварианта берут постусловие .

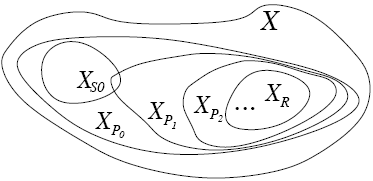
Рассмотрим геометрическую иллюстрацию стоящей перед нами задачи, изобразив на множестве всех значений программных переменных подмножества 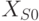и , второе из которых задается постусловием , а первое представляет собой множество, которое может быть получено из после выполнения совокупности простых присваиваний S0. Искомому инварианту цикла на рисунке 8.1 должно соответствовать какое-то неизвестное нам пока множество .

Рис. 8.1. Теория воздушного шарика

Существует весьма красивое описание того, что происходит с множеством переменных программы в процессе выполнения цикла, называемое теорией воздушного шарика. Рассмотрим последовательность предикатов 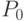, , , , 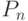описывающих множества переменных до начала цикла, после его первой итерации, , после -ой (последней) итерации.

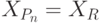Множества, определяемые этими предикатами, представляют последовательность вложенных друг в друга множеств, причем , а . Удобно представлять себе эти множества как последовательные состояния изначально надутого воздушного шарика, из которого на каждой очередной итерации цикла выпускают немного воздуха.

Используя эту модель, можно сказать, что построение инварианта требует так надуть шарик, находящийся в состоянии , чтобы он стал содержать множество 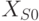. С математической точки зрения необходимо ослабить предикат до такой степени, чтобы истинность этого ослабленного предиката (который и будет взят в качестве инварианта ) могла быть получена из истинного с помощью простых начальных присваиваний S0.

Итак, основным методом построения инварианта является ослабление постусловия оператора цикла. При этом часто удается получить и условие продолжения цикла (что по существу эквивалентно заданию ограничивающей функции), взяв в его качестве отрицание того предиката, которым мы ослабили постусловие.

Реально применяются три первых из следующих ниже приведенных методов построения инварианта.

1. Устранение конъюнктивного члена. Предикат 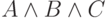можно ослабить до .
2. Замена константы переменной. Предикат

   может быть ослаблен до

   , где — новая переменная.
3. Расширение области значений переменной. Предикат можно ослабить до .
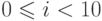4. Добавление дизъюнктивного члена. Предикат можно ослабить до 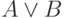, где — некоторый другой предикат.

Причина того, что четвертый метод не применяется, весьма проста — он не содержит никаких рекомендаций по поводу того, как именно выбрать предикат . Остальные методы построения инварианта цикла будут проиллюстрированы в последующих секциях данного параграфа в процессе решения различных задач.