Проектирование цикла при помощи инварианта
Замена константы переменной
В качестве первого примера использования этого метода построения инварианта рассмотрим простую задачу суммирования элементов массива.
Задача 8.3. Напишите программу, находящую сумму  элементов заданного целочисленного
массива
элементов заданного целочисленного
массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) , элементы которого и величину
, элементы которого и величину  изменять нельзя.
Точные пред-
и постусловия:
изменять нельзя.
Точные пред-
и постусловия:  ,
,
![\displaystyle R=\left(s = \sum_{j=0}^{n-1} b[j]\right).](/sites/default/files/tex_cache/925b14b983a8f78ecce564b23e49c49b.png)
Решение
В постусловие входит константа  , которую мы можем заменить
новой переменной
, которую мы можем заменить
новой переменной  , меняющейся в диапазоне от
, меняющейся в диапазоне от  до
до  включительно. Таким образом, метод замены константы переменной
приводит нас к инварианту
включительно. Таким образом, метод замены константы переменной
приводит нас к инварианту
![\displaystyle I=\left(0\leqslant i \leqslant n
\land
\left(s = \sum_{j=0}^{i-1} b[j]\right)\right).](/sites/default/files/tex_cache/11b09ec7d71e7193bf0644dedda8da5a.png)
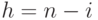 .
.Истинности инварианта легко добиться обнулением величин  и
и  ,
поэтому искомая программа будет иметь вид "i=0;s=0;while(i<n)S;"
с неизвестным нам пока телом цикла S.
,
поэтому искомая программа будет иметь вид "i=0;s=0;while(i<n)S;"
с неизвестным нам пока телом цикла S.
Для того, чтобы цикл завершился, необходимо уменьшать  , что
вполне
естественно делать, увеличивая
, что
вполне
естественно делать, увеличивая  на единицу на каждой итерации
цикла.
Используя инвариант, находим, что вторым необходимым действием является
добавление к
на единицу на каждой итерации
цикла.
Используя инвариант, находим, что вторым необходимым действием является
добавление к  значения
значения ![b[i]](/sites/default/files/tex_cache/9f898d4db67678e874a7aeecdac2d9c5.png) :
:
Текст программы
public class SumArr {
static int b[];
public static void main(String[] args) throws Exception {
int n = Xterm.inputInt("n -> ");
b = new int[n];
for (int k=0; k<n; k++)
b[k] = Xterm.inputInt("b["+k+"] -> ");
int i=0, s=0;
while (i < n) {
s += b[i];
i += 1;
}
Xterm.println("s = " + s);
}
}Докажем ее правильность.
- Так както
![\displaystyle wp("i=0;s=0;",
\left(0\leqslant i \leqslant n \land
\left(s = \sum_{j=0}^{i-1} b[j]\right)\right) =
\\
(0 \leqslant n \land T) = (0 \leqslant n),](/sites/default/files/tex_cache/43ab56708be2b4262c6189f224257ec0.png)
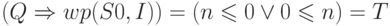 .
. -
![$\displaystyle wp(S, I) = wp\left("s+=b[i];i+=1;",
\left(0\leqslant i \leqslant n \land
\left(s = \sum_{j=0}^{i-1} b[j]\right)\right)\right) =
wp\left("s+=b[i];",
\left(0\leqslant i+1 \leqslant n \land
\left(s = \sum_{j=0}^{i} b[j]\right)\right)\right) =
\Bigl(0\leqslant i+1 \leqslant n\ \land$](/sites/default/files/tex_cache/15706f071e6ca9d483faa5ded6346538.png)
![$\displaystyle \left(s+b[i] = \sum_{j=0}^{i} b[j]\right)\Bigr) =
\left(-1\leqslant i \leqslant n-1 \land
\left(s = \sum_{j=0}^{i-1} b[j]\right)\right).$](/sites/default/files/tex_cache/5cc32abfe8aeb577c67b2576a48cdd81.png)
Теперь вычислим
![\displaystyle (I\land e \Rightarrow wp(S, I)) =
(i<0)\lor(i>n)\lor
!\left(s = \sum_{j=0}^{i-1} b[j]\right)\lor
\\
(i \geqslant n) \lor
\left(-1\leqslant i \leqslant n-1 \land
\left(s = \sum_{j=0}^{i-1} b[j]\right)\right)](/sites/default/files/tex_cache/e4b443ca3dde359c60905f5981445c36.png)
Данный предикат заведомо истинен, если истинен один из первых четырех его дизъюнктивных членов. В противном случае имеем
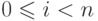 и
и 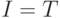 , поэтому
истинен пятый его дизъюнктивный член, следовательно предикат является
тавтологией.
, поэтому
истинен пятый его дизъюнктивный член, следовательно предикат является
тавтологией. -
![\displaystyle (I \land !e) = \left(0\leqslant i \leqslant n \land
\left(s = \sum_{j=0}^{i-1} b[j]\right)\right)\land (i \geqslant n) =
\left(s = \sum_{j=0}^{n-1} b[j]\right) \land (i=n)= (R \land (i=n))](/sites/default/files/tex_cache/ebd3d94989d21641a8033310b23b95cb.png)
Очевидно, что
 .
. -
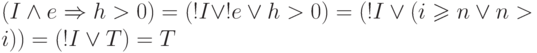 .
. -
![wp("h1=h; S;", h<h1) =
wp("h1=n-i;",wp("s+=b[i];i+=1;",n-i<h1)) =
\\
wp("h1=n-i;",n-i-1<h1)=(n-i-1<n-i)=T](/sites/default/files/tex_cache/cd2754b177945511f38b07707ebc474a.png) .
.
Следовательно,  .
.
Построим более быструю программу нахождения приближенного значения квадратного корня.
Задача 8.4. Напишите программу, находящую приближенное значение квадратного корня  из заданного неотрицательного целого числа
из заданного неотрицательного целого числа  . Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить
. Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить  , таковы:
, таковы:  ,
,  . При написании программы величину
. При написании программы величину  изменять нельзя.
изменять нельзя.
Решение Построим инвариант с помощью метода замены константы  на
переменную
на
переменную  .
Из условия задачи вытекает, что
.
Из условия задачи вытекает, что  ,
следовательно
инвариантом является предикат
,
следовательно
инвариантом является предикат 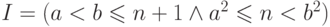 . Условие продолжения цикла легко получается из
того факта,
что предикат
. Условие продолжения цикла легко получается из
того факта,
что предикат  должен быть тавтологией
—
должен быть тавтологией
—  , а это означает использование ограничивающей
функции
, а это означает использование ограничивающей
функции  .
.
После присваиваний "a=0;b=n+1;" предикат  становится
истинным,
следовательно наша программа имеет вид "a=0;b=n+1;while(a+1!=b)S;" с
неизвестным пока телом цикла S.
становится
истинным,
следовательно наша программа имеет вид "a=0;b=n+1;while(a+1!=b)S;" с
неизвестным пока телом цикла S.
Для того чтобы цикл завершился, необходимо уменьшать  , что
эквивалентно
сближению чисел
, что
эквивалентно
сближению чисел  и
и  . Уменьшение разности
. Уменьшение разности  на единицу на каждой
итерации цикла не позволит достичь требуемой в условии задачи эффективности
программы. Нужная временная сложность может быть получена при использовании
метода деления отрезка
на единицу на каждой
итерации цикла не позволит достичь требуемой в условии задачи эффективности
программы. Нужная временная сложность может быть получена при использовании
метода деления отрезка ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) пополам на каждой итерации и выборе
той
из половинок, на которой лежит искомое приближенное значение квадратного
корня. Реализация данной идеи приводит к следующей программе.
пополам на каждой итерации и выборе
той
из половинок, на которой лежит искомое приближенное значение квадратного
корня. Реализация данной идеи приводит к следующей программе.
Текст программы
public class Sqrt3 {
public static void main(String[] args) throws Exception {
int a, b, n;
n = Xterm.inputInt("n -> ");
a = 0;
b = n+1;
while (a+1 != b) {
int c = (a+b)/2;
if (c*c <= n) a = c;
else b = c;
}
Xterm.println("sqrt(" + n + ") = " + a);
}
}Докажите самостоятельно ее правильность и оцените эффективность.
