НОУ ИНТУИТ | Основы теории информации и криптографии. Лекция 6: Арифметическое кодирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 11.04.2007 | Уровень: специалист | Доступ: свободно

|

Вам нравится? Нравится 53 студентам

| Поделиться |

Поддержать программу

Аннотация: В лекции подробно рассматривается арифметическое кодирование. Математическое доказательство его "выгодности" по отношению к другим методам кодирования. Проводится сравнение с другими методами кодирования. Очень хорошо освещены адаптивные алгоритмы сжатия информации, адаптивное арифметическое кодирование. Характерно большое количество примеров и заданий для самостоятельного изучения

Алгоритм кодирования Хаффмена, в лучшем случае, не может передавать на каждый символ сообщения менее одного бита информации. Предположим, известно, что в сообщении, состоящем из нулей и единиц, единицы встречаются в 10 раз чаще нулей. При кодировании методом Хаффмена и на 0 и на 1 придется тратить не менее одного бита. Но энтропия д.с.в., генерирующей такие сообщения $\approx$ 0.469 бит/сим. Неблочный метод Хаффмена дает для минимального среднего количества бит на один символ сообщения значение 1 бит. Хотелось бы иметь такую схему кодирования, которая позволяла бы кодировать некоторые символы менее чем одним битом. Одной из лучших среди таких схем является арифметическое кодирование, разработанное в 70-х годах XX века.

По исходному распределению вероятностей для выбранной для кодирования д.с.в. строится таблица, состоящая из пересекающихся только в граничных точках отрезков для каждого из значений этой д.с.в.; объединение этих отрезков должно образовывать отрезок [0,1] , а их длины должны быть пропорциональны вероятностям соответствующих значений д.с.в. Алгоритм кодирования заключается в построении отрезка, однозначно определяющего данную последовательность значений д.с.в. Затем для построенного отрезка находится число, принадлежащее его внутренней части и равное целому числу, деленному на минимально возможную положительную целую степень двойки. Это число и будет кодом для рассматриваемой последовательности. Все возможные конкретные коды - это числа строго большие нуля и строго меньшие одного, поэтому можно отбрасывать лидирующий ноль и десятичную точку, но нужен еще один специальный код-маркер, сигнализирующий о конце сообщения. Отрезки строятся так. Если имеется отрезок для сообщения длины n-1 , то для построения отрезка для сообщения длины , разбиваем его на столько же частей, сколько значений имеет рассматриваемая д.с.в. Это разбиение делается совершенно также как и самое первое (с сохранением порядка). Затем выбирается из полученных отрезков тот, который соответствует заданной конкретной последовательности длины .

Принципиальное отличие этого кодирования от рассмотренных ранее методов в его непрерывности, т.е. в ненужности блокирования. Код здесь строится не для отдельных значений д.с.в. или их групп фиксированного размера, а для всего предшествующего сообщения в целом. Эффективность арифметического кодирования растет с ростом длины сжимаемого сообщения (для кодирования Хаффмена или Шеннона-Фэно этого не происходит). Хотя арифметическое кодирование дает обычно лучшее сжатие, чем кодирование Хаффмена, оно пока используется на практике сравнительно редко, т.к. оно появилось гораздо позже и требует больших вычислительных ресурсов.

При сжатии заданных данных, например, из файла все рассмотренные методы требуют двух проходов. Первый для сбора частот символов, используемых как приближенные значения вероятностей символов, и второй для собственно сжатия.

Пример арифметического кодирования. Пусть д.с.в. может принимать только два значения 0 и 1 с вероятностями 2/3 и 1/3 соответственно. Сопоставим значению 0 отрезок [0,2/3] , а 1 - [2/3,1] . Тогда для д.с.в. $\vec X$ ,

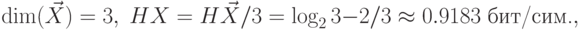
$\dim(\vec X)=3,\; HX=H\vec X/3=\log_23-2/3\approx0.9183\hbox{ бит/сим.},$

таблица построения кодов -

$\smallskip \centerline{\vbox{\offinterlineskip\let~\xfrac \halign{\strut\hfil#& $#$& $#$\hfil\vrule height 11pt& \hfil\ #\ \hfil\vrule&\ #\hfil\cr Интервалы и коды \span \span& Вероятность& Код Хаффмена\cr \noalign{\hrule} && 111[{26\over27},1]\ni{31\over32}=0.11111\kern2pt& $~1{27}$& \quad0000\cr & 11[{8\over9},1]\quad& 110[{8\over9},{26\over27}]\ni{15\over16}=0.1111& $~2{27}$& \quad0001\cr && 101[{22\over27},{8\over9}]\ni{7\over8}=0.111& $~2{27}$& \quad010\cr $1[{2\over3},1]$\quad& 10[{2\over3},{8\over9}]\quad& 100[{2\over3},{22\over27}]\ni{3\over4}=0.11& $~4{27}$& \quad001\cr && 011[{16\over27},{2\over3}]\ni{5\over8}=0.101& $~2{27}$& \quad011\cr & 01[{4\over9},{2\over3}]\quad& 010[{4\over9},{16\over27}]\ni{1\over2}=0.1& $~4{27}$& \quad100\cr && 001[{8\over27},{4\over9}]\ni{3\over8}=0.011& $~4{27}$& \quad101\cr $0[0,{2\over3}]$\quad& 00[0,{4\over9}]\quad& 000[0,{8\over27}]\ni{1\over4}=0.01& $~8{27}$& \quad11.\cr}}} $$ML_1(\vec X)=65/81\approx0.8025\hbox{ бит/сим. (арифметическое),}$$ $$ML_1(\vec X)=76/81\approx0.9383\hbox{ бит/сим. (блочный Хаффмена),}$$ $$ML_1(X)=ML(X)=1\hbox{ бит/сим. (Хаффмена).}$$$

Среднее количество бит на единицу сообщения для арифметического кодирования получилось меньше, чем энтропия. Это связано с тем, что в рассмотренной простейшей схеме кодирования, не описан код-маркер конца сообщения, введение которого неминуемо сделает это среднее количество бит большим энтропии.

Получение исходного сообщения из его арифметического кода происходит по следующему алгоритму.

Шаг 1. В таблице для кодирования значений д.с.в. определяется интервал, содержащий текущий код, - по этому интервалу однозначно определяется один символ исходного сообщения. Если этот символ - это маркер конца сообщения, то конец.

Шаг 2. Из текущего кода вычитается нижняя граница содержащего его интервала, полученная разность делится на длину этого же интервала. Полученное число считается новым текущим значением кода. Переход к шагу 1.

Рассмотрим, например, распаковку сообщения 111. Этому сообщению соответствует число $7/8\in[2/3,1]$ , что означает, что первый знак декодируемого сообщения - это 1. Далее от 7/8 вычитается 2/3 и результат делится на 1/3, что дает $5/8\in[0,2/3]$ , что означает, что следующий знак - 0. Теперь, вычислив $(5/8-0)*3/2=15/16\in[2/3,1]$ , получим следующий знак - 1, т.е. все исходное сообщение 101 декодировано. Однако, из-за того, что условие остановки не определенно, алгоритм декодирования здесь не остановится и получит "следующий символ" 1 и т.д.

Упражнение 20 Вычислить среднее количество бит на единицу сжатого сообщения о значении каждой из д.с.в., из заданных следующими распределениями вероятностей, при сжатии методами Шеннона-Фэно, Хаффмена и арифметическим. Арифметический код здесь и в следующих упражнениях составлять, располагая значения д.с.в. в заданном порядке слева-направо вдоль отрезка от 0 до 1.

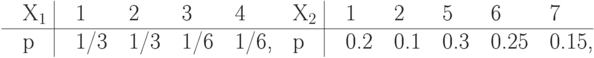
$\line{\hss\vbox{\offinterlineskip\halign{&\strut\quad#\cr X_1& \omit\ \vrule& 1& 2& 3& 4\cr \noalign{\hrule} p& \omit\ \vrule& 1/3& 1/3& 1/6& 1/6,\cr}}\hss \vbox{\offinterlineskip\halign{&\strut\quad#\cr X_2& \omit\ \vrule& 1& 2& 5& 6& 7\cr \noalign{\hrule} p& \omit\ \vrule& 0.2& 0.1& 0.3& 0.25& 0.15,\cr}}\hss}$

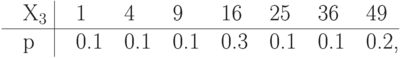
$\centerline{\vbox{\offinterlineskip\halign{&\strut\quad#\cr X_3& \omit\ \vrule& 1& 4& 9& 16& 25& 36& 49\cr \noalign{\hrule} p& \omit\ \vrule& 0.1& 0.1& 0.1& 0.3& 0.1& 0.1& 0.2,\cr}}}$

$\centerline{\vbox{\offinterlineskip\halign{&\strut\quad#\cr X_4& \omit\ \vrule& -2& -1& 0& 1& 2\cr \noalign{\hrule} p& \omit\ \vrule& 1/3& 1/4& 1/5& 1/6& 1/20.\cr}}}$

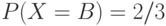Упражнение 21 Вычислить длины кодов Хаффмена и арифметического для сообщения AAB, полученного от д.с.в. со следующим распределением вероятностей P(X=A)=1/3 , P(X=B)=2/3 .

Упражнение 22 Декодировать арифметический код 011 для последовательности значений д.с.в. из предыдущего упражнения. Остановиться, после декодирования третьего символа.

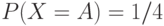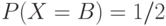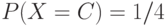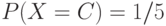Упражнение 23 Составить арифметический код для сообщения BAABC, полученного от д.с.в. со следующим распределением вероятностей P(X=A)=1/4 , P(X=B)=1/2 , P(X=C)=1/4 . Каков будет арифметический код для этого же сообщения, если распределена по закону P(X=A)=1/3 , P(X=B)=7/15 , P(X=C)=1/5 ?

Упражнение 24 д.с.в. может принимать три различных значения. При построении блочного кода с длиной блока 4 для необходимо будет рассмотреть д.с.в. $\vec X$ - выборку четырех значений . Сколько различных значений может иметь $\vec X$ ? Если считать сложность построения кода пропорциональной количеству различных значений кодируемой д.с.в., то во сколько раз сложнее строить блочный код для по сравнению с неблочным?

Упражнение 25 Составить коды Хаффмена, блочный Хаффмена (для блоков длины 2 и 3) и арифметический для сообщения ABAAAB, вычислить их длины. Приблизительный закон распределения вероятностей д.с.в., сгенерировавшей сообщение, определить анализом сообщения.

Дальше >>

Авторизоваться

Основы теории информации и криптографии

Арифметическое кодирование

Вопросы и ответы