НОУ ИНТУИТ | Основы теории информации и криптографии. Лекция 4: Элементы теории чисел

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 11.04.2007 | Уровень: специалист | Доступ: свободно

|

Вам нравится? Нравится 53 студентам

| Поделиться |

Поддержать программу

Ключевые слова: Каноническим разложением, Функцией Эйлера, отображение, взаимно простыми, функция, равенство, место, ПО, алгоритму Евклида, остаток, числитель, таблица, гипотеза, труднорешаемой

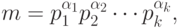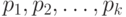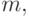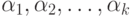Каноническим разложением числа называется разложение его на простые сомножители в виде $m=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k},$ где $p_1,p_2,\ldots,p_k$ - все различные простые делители числа а $\alpha_1,\alpha_2,\ldots,\alpha_k$ - целые положительные числа.

Функцией Эйлера называется, отображение $\varphi\colon\bN\rightarrow\bN,$

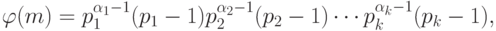
$\varphi(m)=p_1^{\alpha_1-1}(p_1-1)p_2^{\alpha_2-1}(p_2-1)\cdots p_k^{\alpha_k-1}(p_k-1),$

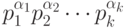$p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}$ - каноническое разложение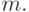

Например, 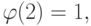$\varphi(2)=1,$ $\varphi(12)=\varphi(2^23)=2^1(2-1)3^0(3-1)=2*2=4,$ $\varphi(1000)=\varphi(2^35^3)=2^25^24=4*25*4=400.$

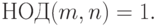
Числа и называются взаимно простыми, если у них нет общих делителей больших 1, т.е. $\hbox{НОД}(m,n)=1.$

Функция Эйлера от числа равна числу чисел меньших и взаимно простых с m [6].

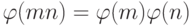Для взаимно простых и верно равенство $\varphi(mn)=\varphi(m)\varphi(n)$ [6].

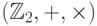Число примитивных многочленов степени над полем $(\bZ_2,+,\times)$ равно $\varphi(2^n-1)/n$ [12].

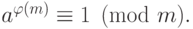
Теорема Эйлера-Ферма¹¹². Для взаимно простых и имеет место соотношение $a^{\varphi(m)}\equiv1\pmod m.$

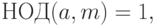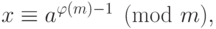Для решения уравнения $ax\equiv1\pmod m,$ где $\hbox{НОД}(a,m)=1,$ можно использовать теорему Эйлера-Ферма, т.е. $x\equiv a^{\varphi(m)-1}\pmod m,$ но это весьма трудоемкий способ. Получим решения искомого уравнения через формулу для решения эквивалентного уравнения ax-my=1.

По алгоритму Евклида для получения НОД двух заданных чисел нужно одно число делить на другое, затем делить делитель на получаемый остаток до тех, пока остаток не станет равным нулю. Последний больший нуля остаток будет искомым НОД.

Для чисел и последовательность шагов алгоритма Евклида выглядит как

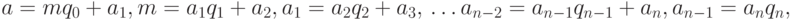
$\eqalign{a&=mq_0+a_1,\cr\\ m&=a_1q_1+a_2,\cr\\ a_1&=a_2q_2+a_3,\cr\\ &\dots\cr\\ a_{n-2}&=a_{n-1}q_{n-1}+a_n,\cr\\ a_{n-1}&=a_nq_n,\cr}$

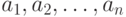где $a_1,a_2,\ldots,a_n$ - остатки. Разложение $\displaystyle{a\over m}$ в цепную дробь по последовательности частных

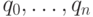
$q_0,\ldots,q_n$

имеет вид

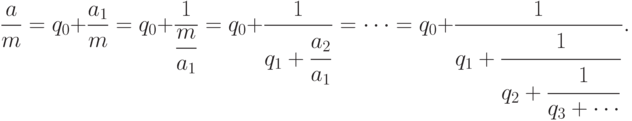
${a\over m}=q_0+{a_1\over m}=q_0+{1\over\displaystyle{m\over a_1}}= q_0+{1\over\displaystyle q_1+ {\strut a_2\over a_1}}= \cdots = q_0+{1\over\displaystyle q_1+ {\strut1\over\displaystyle q_2+ {\strut1\over\displaystyle q_3+\cdots}}}.$

Обозначим за P_k/Q_k

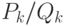дробь, получаемую из приведенной цепной дроби отбрасыванием членов с индексами, большими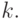

Например,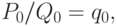

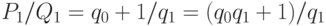и т.д. Числитель, P_k,

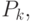и знаменатель, Q_k,

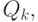можно вычислять рекуррентно по следующим формулам: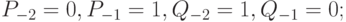

$P_{-2}=0, P_{-1}=1, Q_{-2}=1, Q_{-1}=0;$

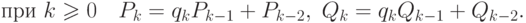
$\hbox{при }k\ge0\quad P_k=q_kP_{k-1}+P_{k-2},\; Q_k=q_kQ_{k-1}+Q_{k-2}.$

По определению P_n=a

и

Кроме того,

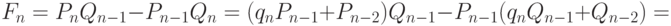
$F_n=P_nQ_{n-1}-P_{n-1}Q_n= (q_nP_{n-1}+P_{n-2})Q_{n-1}-P_{n-1}(q_nQ_{n-1}+Q_{n-2})=$

$=-P_{n-1}Q_{n-2}+P_{n-2}Q_{n-1}=-F_{n-1}=\cdots=F_{n-2}=\cdots= (-1)^{n+1}F_{-1}=$

$=(-1)^{n+1}(P_{-1}Q_{-2}-P_{-2}Q_{-1})=(-1)^{n+1}$

или

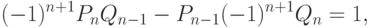
$(-1)^{n+1}P_nQ_{n-1}-P_{n-1}(-1)^{n+1}Q_n=1,$

что означает

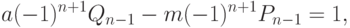
$a(-1)^{n+1}Q_{n-1}-m(-1)^{n+1}P_{n-1}=1,$

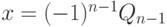т.е. $x=(-1)^{n-1}Q_{n-1}$ и $y=(-1)^{n-1}P_{n-1}.$

Процесс получения числителей и знаменателей удобно оформить в виде таблицы:

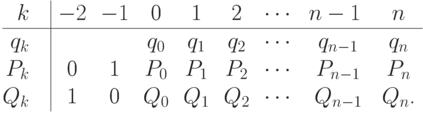
$\smallskip \centerline{\vbox{\offinterlineskip \halign{\strut\hfil#\quad\vrule&&\ \hfil#\ \hfil\cr $k$& $-2$& $-1$& 0& 1& 2& $\cdots$& $n-1$ & $n$\cr \noalign{\hrule} $q_k$& \omit& \omit& $q_0$& $q_1$& $q_2$& $\cdots$& $q_{n-1}$& $q_n$\cr $P_k$& 0& 1& $P_0$& $P_1$& $P_2$& $\cdots$& $P_{n-1}$& $P_n$\cr $Q_k$& 1& 0& $Q_0$& $Q_1$& $Q_2$& $\cdots$& $Q_{n-1}$& $Q_n$.\cr}}} \smallskip$

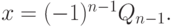
Таким образом, корни уравнения $ax\equiv1\pmod m$ вычисляются по формуле $x=(-1)^{n-1}Q_{n-1}.$

Пример. Решить уравнение $1181x\equiv1\pmod{1290816}.$ Сначала по алгоритму Евклида получается следующая цепочка соотношений:

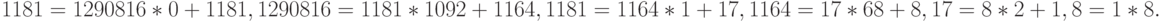
$\eqalign{1181&=1290816*0+1181,\cr\\ 1290816&=1181*1092+1164,\cr\\ 1181&=1164*1+17,\cr\\ 1164&=17*68+8,\cr\\ 17&=8*2+1,\cr\\ 8&=1*8.\cr}$

Затем составляется таблица для вычисления Q_5

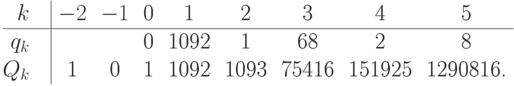
$\smallskip \centerline{\vbox{\offinterlineskip \halign{\strut\hfil#\quad\vrule&&\ \hfil#\ \hfil\cr $k$& $-2$& $-1$& 0& 1& 2& 3& 4& 5\cr \noalign{\hrule} $q_k$& \omit& \omit& 0& 1092& 1& 68& 2& 8\cr $Q_k$& 1& 0& 1& 1092& 1093& 75416& 151925& 1290816.\cr}}} \smallskip$

Таким образом, искомый равен 151925.

Гипотеза. Задача разложения целого числа с заданным числом разрядов на множители является труднорешаемой

Задача называется труднорешаемой, если время ее решения зависит от объема входных данных по экспоненциальному закону и не может быть сведено к полиномиальному}.

На сегодняшний день существуют весьма быстрые алгоритмы для проверки данного числа на простоту, но для разложения 200-значного числа на множители лучшим современным компьютерам по лучшим современным алгоритмам может потребоваться миллиарды лет.

Эта гипотеза лежит в основе методов Диффи-Хеллмана.

Дальше >>

Авторизоваться

Основы теории информации и криптографии

Элементы теории чисел

Вопросы и ответы