НОУ ИНТУИТ | Прикладная статистика. Лекция 11: Статистика нечисловых данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать программу

Аннотация: Описывается структура статистики нечисловых данных и ее использование в экспертных оценках. Рассматривается теория случайных толерантностей, люсианов, метод парных сравнений, статистика нечетких множеств.

Ключевые слова: статистика, программа, множества, ПО, дискретное распределение, группа, экспертные оценки, анализ, разделы, значение, функция, определение, математическим ожиданием, закон больших чисел, окрестность, вероятность, доказательство, обобщение, оценка максимального правдоподобия, факторный анализ, компонент, сходимость, мера, множитель, вывод, шкала, прямой, тождественное преобразование, шкала отношений, АСУ, шкала измерений, оценивание, вектор, испытание Бернулли, объект, длина, объединение, расстояние, связь, представление, место, метрика, очередь, принятия решений, отношение, Главная диагональ, случайная величина, биномиальное распределение, координаты, матрица, нормальное распределение, гипотеза, дисперсия, мощность критерия, Квантиль, медиана, минимум, объем выборки, дисперсионный анализ, размерность, константы, отрицание, метод статистических испытаний, подмножество, вычисление, равенство, коэффициенты, гиперкуб, скалярное произведение, выход, разбиение, ядро, кластер, диаметр, модуль, вероятностная модель, пространство, итеративный метод, деятельность, команда, опрос, ранжирование, структурная схема, значимость, линейная модель, единица, метод наименьших квадратов, производные, свободными членами, адекватность модели, функция принадлежности, нечеткое множество, нечеткое число, погрешность, нечеткая переменная, минимизация, алгоритм, дендрограмма, ветвь, Шаг работы алгоритма, монотонная функция, дерево, максимум, оптимизация, куча, работ, ранг, подразделения, запись, слово, определение проекта, менеджмент, фигурные скобки, бинарным отношением, отношение эквивалентности, класс эквивалентности, эквивалентность, граф, ребро, неравенство, корректность, полный граф, статистические методы, фирма, математика, исключение, аргумент, метод экспертных оценок, отношение сходства, случайная выборка, целочисленное программирование, метод ветвей и границ, кластерный анализ

11.1. Структура статистики нечисловых данных

Статистика нечисловых данных или, как ее еще называют, статистика объектов нечисловой природы была выделена в нашей стране как самостоятельное научное направление. Как уже отмечалось, термин "статистика объектов нечисловой природы" впервые появился в 1979 г. в монографии [ [ 1.15 ] ]. В том же году в работе [ [ 11.21 ] ] была сформулирована программа развития этого нового направления прикладной статистики.

Со второй половины 80-х годов существенно возрос интерес к этой тематике и у зарубежных исследователей. Это нашло отражение, в частности, на Первом Всемирном Конгрессе Общества математической статистики и теории вероятностей им. Бернулли, состоявшемся в сентябре 1986 г. в Ташкенте. Статистика объектов нечисловой природы используется в нормативно-технической и методической документации, ее применение позволяет получить существенный технико-экономический эффект (сводка дана, например, в статье [ [ 11.12 ] ]).

Цель настоящего параграфа - ввести в статистику нечисловых данных, выделить ее структуру, указать основные идеи и результаты.

Напомним, что объектами нечисловой природы называют элементы пространств, не являющихся линейными. Примерами являются бинарные отношения (ранжировки, разбиения, толерантности), множества, последовательности символов (тексты). Объекты нечисловой природы нельзя складывать и умножать на числа, не теряя при этом содержательного смысла. Этим они отличаются от издавна используемых в прикладной статистике (в качестве элементов выборок) чисел, векторов и функций.

Прикладную статистику по виду статистических данных принято делить на следующие направления:

статистика случайных величин (одномерная статистика);
многомерный статистический анализ;
статистика временных рядов и случайных процессов;
статистика нечисловых данных (ее важная часть - статистика интервальных данных).

При создании теории вероятностей и математической статистики исторически первыми были рассмотрены объекты нечисловой природы - белые и черные шары в урне. На основе соответствующих вероятностных моделей были введены биномиальное, гипергеометрическое и другие дискретные распределения. Получены теоремы Муавра-Лапласа, Пуассона и др. Современное развитие этой тематики привело, в частности, к созданию теории статистического контроля качества продукции по альтернативному признаку (годен - не годен) в работах А.Н. Колмогорова, Б.В. Гнеденко, Ю.К. Беляева, Я.П. Лумельского и многих других (см., например, [ [ 11.2 ] , [ 11.14 ] ]).

В семидесятых годах ХХ в. в связи с запросами практики весьма усилился интерес к статистическому анализу нечисловых данных. Московская группа, организованная Ю.Н. Тюриным и другими специалистами вокруг созданного в 1973 г. научного семинара "Экспертные оценки и нечисловая статистика", развивала в основном вероятностную статистику нечисловых данных. Были установлены разнообразные связи между различными видами объектов нечисловой природы и изучены свойства этих объектов. Московской группой выпущены десятки сборников и обзоров, перечень которых приведен в итоговой работе [ [ 11.21 ] ]. Хотя в названиях многих из этих изданий стоят слова "экспертные оценки", анализ содержания сборников показывает, что подавляющая часть статей посвящена математико-статистическим вопросам, а не проблемам проведения экспертиз. Частое употребление указанных слов отражает лишь один из импульсов, стимулирующих развитие статистики объектов нечисловой природы и идущих от запросов практики. При этом необходимо подчеркнуть, что полученные результаты могут и должны активно использоваться в теории и практике экспертных оценок.

Новосибирская группа (Г.С. Лбов, Б.Г. Миркин и др.), как правило, не использовала вероятностные модели, т.е. вела исследования в рамках анализа данных. В московской группе в рамках анализа данных также велись работы, в частности, Б.Г.Литваком. Исследования по статистике объектов нечисловой природы выполнялись также в Ленинграде, Ереване, Киеве, Таллинне, Тарту, Красноярске, Минске, Днепропетровске, Владивостоке, Калинине и других отечественных научных центрах.

Внутреннее деление статистики объектов нечисловой природы. Внутри рассматриваемого направления прикладной статистики выделяют следующие области.

статистика конкретных видов объектов нечисловой природы;
статистика в пространствах общей (произвольной) природы;
применение идей, подходов и результатов статистики объектов нечисловой природы в классических областях прикладной статистики.

Единство рассматриваемому направлению придает прежде всего вторая составляющая, позволяющая с единой точки зрения подходить к статистическим задачам описания данных, оценивания, проверки гипотез при рассмотрении выборки, элементы которой имеют ту или иную конкретную природу. Внутри первой составляющей рассматривают:

теорию измерений;
статистику бинарных отношений;
теорию люсианов (бернуллиевских векторов);
статистику случайных множеств;
статистику нечетких множеств;
аксиоматическое введение метрик;
многомерное шкалирование и кластер-анализ (существенную часть этой тематики относят также к многомерному статистическому анализу).

Перечисленные разделы тесно связаны друг с другом, как продемонстрировано, в частности, в работах [ [ 11.5 ] , [ 1.15 ] ] и предыдущих лекциях настоящего курса. Вне данного перечня остались работы по хорошо развитым классическим областям - статистическому контролю, таблицам сопряженности, а также по анализу текстов и некоторые другие (см. [ [ 11.21 ] , [ 2.15 ] , [ 11.35 ] ]). Таким образом, кратко рассмотрим постановки вероятностной статистики объектов нечисловой природы (1970-2005 гг.), чтобы представить как единое целое это направление прикладной статистики.

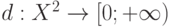Статистика в пространствах общей природы. Пусть x_1,x_2,...,x_n - элементы пространства , не являющегося линейным. Как определить среднее значение для ? Поскольку нельзя складывать элементы и сравнивать их по величине, то необходимы подходы, принципиально новые по сравнению с классическими. В статистике объектов нечисловой природы предложено использовать показатель различия $d:X^2\rightarrow[0;+\infty)$ (содержательный смысл показателя различия: чем больше 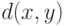d(x,y) , тем больше различаются и ) и определять эмпирическое среднее как решение экстремальной задачи

$E_n(d)=Arg\min\left\{\sum_{1\le i\le n}d(x_i,x), x\in X\right\}.$

( 1)

Таким образом, среднее 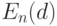E_n(d) - это совокупность всех тех $x\in X$ , для которых функция

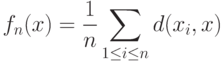$f_n(x)=\frac{1}{n}\sum_{1\le i\le n}d(x_i,x)$

( 2)

достигает минимума на

.

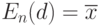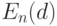Как известно, для классического случая X = R^1 при d(x,y) = (x-y)^2 имеем $E_n(d) = \overline{x}$ . При X = R^1, d(x,y)=|x-y| среднее E_n(d) при нечетном объеме выборки совпадает с выборочной медианой. А при четном объеме - 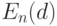E_n(d) является отрезком с концами в двух средних элементах вариационного ряда.

Для ряда конкретных объектов среднее как решение экстремальной задачи вводилось рядом авторов. В 1929 г. итальянские статистики Джини и Гальвани применили такой подход для усреднения точек на плоскости и в пространстве. Американский исследователь Джон Кемени решение задачи (1) называл медианой или средним для выборки, состоящей из ранжировок (см. монографию [ [ 11.9 ] ]). При моделировании лесных пожаров согласно выражению (1) было введено "среднеуклоняемое множество" для описания средней выгоревшей площади (см. об этом в монографии [ [ 1.15 ] ]). Общее определение эмпирических средних вида (1) было впервые введено в работе [ [ 11.21 ] ].

Основной результат, связанный со средними вида (1) - аналог закона больших чисел. Пусть x_1,x_2,..., x_n - независимые одинаково распределенные случайные элементы со значениями в пространстве общей природы . Теоретическим средним, или математическим ожиданием, в статистике объектов нечисловой природы называют

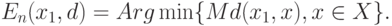$E_n(x_1,d)=Arg\min\{Md(x_1,x),x\in X\}.$

( 3)

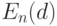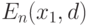Закон больших чисел состоит в сходимости E_n(d) к E_n(x_1,d) при $n\rightarrow\infty$ . Поскольку и эмпирическое, и теоретическое средние - множества, то понятие сходимости требует уточнения.

Одно из возможных уточнений, впервые введенное в работе [ [ 11.21 ] ], таково. Для функции

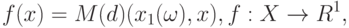$f(x)=M(d)(x_1(\omega),x), f:X\rightarrow R^1,$

( 4)

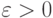введем понятие " $\varepsilon$ -пятки" ( $\varepsilon>0$ )

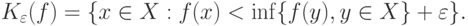$K_{\varepsilon}(f)=\{x\in X:f(x)<\inf\{f(y),y\in X\}+\varepsilon\}.$

( 5)

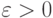Очевидно, $\varepsilon$ -пятка - это окрестность $Arg\min(f)$ (если он достигается), заданная в терминах минимизируемой функции. Тем самым снимается вопрос о выборе метрики в пространстве . Тогда при некоторых условиях регулярности для любого $\varepsilon>0$ вероятность события

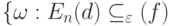$\{\omega:E_n(d)\subseteq\K_{\varepsilon}(f)}$

( 6)

стремится к 1 при $n\rightarrow\infty$ , т.е. справедлив закон больших чисел. Подробное доказательство приведено в "Описание данных" .

Естественное обобщение рассматриваемой задачи позволяет построить общую теорию оптимизационного подхода в статистике. Как известно, большинство задач прикладной статистики может быть представлено в качестве оптимизационных. Как себя ведут решения экстремальных задач? Частные случаи этой постановки: как ведут себя при росте объема выборки оценки максимального правдоподобия и минимального контраста (в том числе робастные в смысле Тьюки-Хьюбера - см. "Оценивание" )? Что можно сказать о поведении оценок нагрузок в факторном анализе и методе главных компонент при отсутствии нормальности, об оценках метода наименьших модулей в регрессии и т.д.?

Обычно легко устанавливается, что для некоторых пространств и последовательности случайных функций f_n(x) при $n\rightarrow\infty$ найдется функция f(x) такая, что

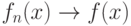$f_n(x)\rightarrow f(x)$

( 7)

для любого $x\in X$ (сходимость по вероятности). Требуется вывести отсюда, что

$Arg\min f_n(x)\rightarrow Arg\min f(x),$

( 8)

т.е. решения экстремальных задач также сходятся. Понятие сходимости в соотношении (8) уточняется, например, с помощью $\varepsilon$ -пяток, как это сделано выше для закона больших чисел. Условия регулярности, при которых справедливо предельное соотношение (8), приведены в исследовании [ [ 1.17 ] ]. Практически для всех реальных задач эти условия выполняются.

Как оценить распределение случайного элемента в пространстве общей природы? Поскольку понятие функции распределения неприменимо, естественно использовать непараметрические оценки плотности. Что такое плотность распределения вероятностей в пространстве произвольной природы? Это функция 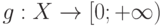$g:X\rightarrow[0;+\infty)$ такая, что для любого измеримого множества (т.е. случайного события) 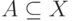$A\subseteq X$ справедливо соотношение

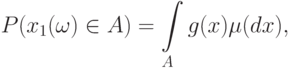$P(x_1(\omega)\in A)=\int\limits_A g(x)\mu(dx),$

( 9)

где $\mu$ - некоторая мера в

. Ряд непараметрических оценок плотности был предложен в работе [ [ 11.21 ] ]. Например, ядерной оценкой плотности является оценка

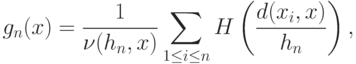$g_n(x)=\frac{1}{\nu(h_n,x)}\sum_{1\le i\le n} H\left(\frac{d(x_i,x)}{h_n}\right),$

( 10)

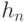где - показатель различия; - ядерная функция; h_n - последовательность положительных чисел; 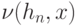$\nu(h_n, x)$ - нормирующий множитель. Удалось установить, что статистики типа (10) обладают такими же свойствами, по крайней мере при фиксированном , что и их классические аналоги при X = R^1 . В частности, такой же скоростью сходимости. Некоторые изменения необходимы при рассмотрении дискретных , каковыми являются многие пространства конкретных объектов нечисловой природы (см. "Описание данных" ). С помощью непараметрических оценок плотности можно развивать регрессионный анализ, дискриминантный анализ и другие направления в пространствах общей природы.

Для проверки гипотез согласия, однородности, независимости в пространствах общей природы могут быть использованы статистики интегрального типа

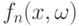$\int f_n(x,\omega)dF_n(x,\omega),$

( 11)

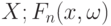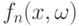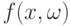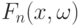где $f_n(x,\omega)$ - последовательность случайных функций на $X; F_n(x,\omega)$ - последовательность случайных распределений (или зарядов). Обычно $f_n(x,\omega)$ при $n\rightarrow\infty$ сходится по распределению к некоторой случайной функции $f(x,\omega)$ , а $F_n(x,\omega)$ - к распределению F(x)

. Тогда распределение статистики интегрального типа (11) сходится к распределению случайного элемента

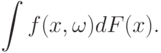$\int f(x,\omega)dF(x).$

( 12)

Условия, при которых это справедливо, даны в "Проверка гипотез" на основе работы [ [ 4.19 ] ]. Пример применения - вывод предельного распределения статистики типа омега-квадрат для проверки симметрии распределения (см. "Статистический анализ числовых величин" ).

Перейдем к статистике конкретных видов объектов нечисловой природы.

Теория измерений. Цель теории измерений - борьба с субъективизмом исследователя при приписывании численных значений реальным объектам. Так, расстояния можно измерять в верстах, аршинах, саженях, метрах, микронах, милях, парсеках и других единицах измерения. Выбор единиц измерения зависит от исследователя, т.е. субъективен. Статистические выводы могут быть адекватны реальности только тогда, когда они не зависят от того, какую именно единицу измерения предпочтет исследователь, т.е. когда они инвариантны относительно допустимого преобразования шкалы.

Теория измерений известна в нашей стране уже более 30 лет. С начала семидесятых годов активно работают отечественные исследователи. В настоящее время изложение основ теории измерений включают в справочные издания, помещают в научно-популярные журналы и книги для детей. Однако она еще не стала общеизвестной среди специалистов, в частности, среди метрологов. Поэтому опишем одну из задач теории измерений (см. "Статистический анализ числовых величин" ).

Как известно, шкала задается группой допустимых преобразований (прямой в себя). Номинальная шкала (шкала наименований) задается группой всех взаимнооднозначных преобразований, шкала порядка - группой всех строго возрастающих преобразований. Это - шкалы качественных признаков. Группа линейных возрастающих преобразований $\varphi(x)=ax+b,a>0$ , задает шкалу интервалов. Группа $\varphi(x)=ax,a>0$ определяет шкалу отношений. Наконец, группа, состоящая из одного тождественного преобразования, описывает абсолютную шкалу. Это - шкалы количественных признаков. Используют и некоторые другие шкалы.

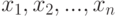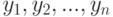Практическую пользу теории измерений обычно демонстрируют на примере задачи сравнения средних значений для двух совокупностей одинакового объема x_1, x_2,...,x_n и y_1, y_2,...,y_n . Пусть среднее вычисляется с помощью функции $f:R^n\rightarrow R^1$ . Если

f(x_1, x_2,...,x_n)<f(y_1, y_2,...,y_n),

( 13)

то необходимо, чтобы

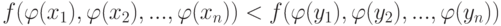$f(\varphi(x_1),\varphi(x_2),...,\varphi(x_n))<f(\varphi(y_1),\varphi(y_2),...,\varphi(y_n))$

( 14)

для любого допустимого преобразования $\varphi$ из задающей шкалу группы $\Phi$ . (В противном случае результат сравнения будет зависеть от того, какое из эквивалентных представлений шкалы выбрал исследователь.)

Требование равносильности неравенств (13) и (14) вместе с некоторыми условиями регулярности приводят к тому, что в порядковой шкале в качестве средних можно использовать только члены вариационного ряда, в частности, медиану, но нельзя использовать среднее геометрическое, среднее арифметическое, и т.д. В количественных шкалах это требование выделяет из всех обобщенных средних по А.Н. Колмогорову в шкале интервалов - только среднее арифметическое, а в шкале отношений - только степенные средние. Кроме средних, аналогичные задачи рассмотрены в статистике нечисловых данных для расстояний, мер связи случайных признаков и других процедур анализа данных.

Приведенные результаты о средних величинах применялись, например, при проектировании системы датчиков в АСУ ТП доменных печей. Велико прикладное значение теории измерений в задачах стандартизации и управления качеством, в частности, в квалиметрии. Так, В.В. Подиновский показал, что любое изменение коэффициентов весомости единичных показателей качества продукции приводит к изменению упорядочения изделий по средневзвешенному показателю, а Н.В. Хованов развил одну из возможных теорий шкал измерения качества. Теория измерений полезна и в других прикладных областях.

Статистика бинарных отношений. Оценивание центра распределения случайного бинарного отношения проводят обычно с помощью медианы Кемени. Состоятельность вытекает из закона больших чисел [ [ 1.15 ] ]. Разработаны различные вычислительные процедуры нахождения медианы Кемени.

Методы проверки гипотез развиты отдельно для каждой разновидности бинарных отношений. В области статистики ранжировок, или ранговой корреляции, классической является книга Кендалла [ [ 11.10 ] ]. Современные достижения отражены в работах Ю.Н. Тюрина и Д.С. Шмерлинга. Статистика случайных разбиений развита А.В. Маамяги. Статистика случайных толерантностей (рефлексивных симметричных отношений) впервые изложена в работе [ [ 1.15 ] ]. Многие ее задачи являются частными случаями задач теории люсианов.

Теория люсианов (бернуллиевских векторов). Люсиан (бернуллиевский вектор) - это последовательность испытаний Бернулли с, вообще говоря, различными вероятностями успеха. Реализация люсиана (бернуллиевского вектора) - это последовательность из 0 и 1. Люсианы (бернуллиевские вектора) рассматривались при статистическом анализе случайных множеств с независимыми элементами, а также результатов независимых парных сравнений. Последовательность результатов контроля качества последовательности единиц продукции по альтернативному признаку - также реализация люсиана (бернуллиевского вектора). Случайная толерантность может быть записана в виде люсиана. Поскольку один и тот же математический объект необходим в различных областях, естественно для его наименования применять специально введенный термин "бернуллиевский вектор". Используется также более краткий термин "люсиан".

В рассматриваемой теории изучают методы проверки согласованности (одинаковой распределенности), однородности двух выборок, независимости люсианов. Методы проверки указанных гипотез нацелены на ситуацию, когда число бернуллиевских векторов фиксировано, а их длина растет. При этом число неизвестных параметров возрастает пропорционально объему данных, т.е. теория построена в асимптотике растущего числа параметров. Ранее подобная асимптотика под названием асимптотики А.Н. Колмогорова использовалась в дискриминантном анализе, но там применялись совсем другие методы для решения иных задач прикладной статистики.

Непараметрическая теория парных сравнений (в предположении независимости результатов отдельных сравнений) - часть теории бернуллиевских векторов. Параметрическая теория связана в основном с попытками выразить вероятности того или иного исхода через значения гипотетических или реальных параметров сравниваемых объектов. Известны модели Терстоуна, Бредли-Терри-Льюса и др. В нашей стране построен ряд новых моделей парных сравнений. В частности, имеются модели парных сравнений с тремя исходами (больше, меньше, неразличимо), модели зависимых сравнений, сравнений нескольких объектов (сближающие рассматриваемую область с теорией случайных ранжировок) и т.д.

Статистика случайных и нечетких множеств. Давнюю историю имеет статистика случайных геометрических объектов (отрезков, треугольников, кругов и т.д.). Современная теория случайных множеств сложилась при изучении пористых сред и объектов сложной природы в таких областях, как металлография, петрография, биология. Различные направления внутри этой теории рассмотрены в работе [ [ 1.15 ] , гл.4]. Остановимся на двух.

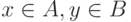Случайные множества, лежащие в евклидовом пространстве, можно складывать: сумма множеств и - это объединение всех векторов x+y , где $x\in A, y\in B$ Н.Н. Ляшенко получил аналоги законов больших чисел, Центральной предельной теоремы, ряда методов прикладной статистики, систематически используя подобные суммы.

Для статистики объектов нечисловой природы интереснее подмножества пространств, не являющихся линейными. В работе [ [ 1.15 ] ] рассмотрены некоторые задачи теории конечных случайных множеств. Позже ряд интересных результатов получил С.А. Ковязин, в частности, он доказал нашу гипотезу о справедливости закона больших чисел при использовании расстояния между множествами

$d(a,b)=\mu(A\Delta B),$

( 15)

где $\mu$ - некоторая мера; $\Delta$ - знак симметрической разности. Расстояние (15) выведено из некоторой системы аксиом в монографии [ [ 1.15 ] ]. Прикладники также делают попытки развивать и применять методы статистики случайных множеств.

С теорией случайных множеств тесно связана теория нечетких множеств, начало которой положено статьей Л.А. Заде в 1965 г. Это направление прикладной математики получило бурное развитие - к настоящему времени число публикаций измеряется десятками тысяч, выпускаются международные журналы, постоянно проводятся конференции, практические приложения дали ощутимый технико-экономический эффект. При изложении теории нечетких множеств обычно не подчеркивается связь с вероятностными моделями. Между тем еще в первой половине 1970-х годов было установлено [ [ 1.15 ] ], что теория нечеткости в определенном смысле сводится к теории случайных множеств, хотя эта связь, возможно, имеет лишь теоретическое значение (см. 4.6).

С точки зрения статистики нечисловых данных нечеткие множества - лишь один из видов объектов нечисловой природы. Поэтому к ним применима общая теория, развитая для пространств произвольной природы. Имеются работы, в которых совместно используются соображения вероятности и нечеткости [ [ 1.16 ] ].

Многомерное шкалирование и аксиоматическое введение метрик. Многомерное шкалирование имеет целью представление объектов точками в пространстве небольшой размерности (1-3) с максимально возможным сохранением расстояний между точками (см. 9.6).

Из сказанного выше ясно, какое большое место занимают в статистике объектов нечисловой природы метрики (расстояния). Как их выбрать? Предлагают выводить вид метрик из некоторых систем аксиом. Аксиоматически получена метрика в пространстве ранжировок, которая оказалась линейно связанной с коэффициентом ранговой корреляции Кендалла. Метрика (15) в пространстве множеств получена в работе [ [ 2.1 ] ] также исходя из некоторой системы аксиом. Г.В. Раушенбахом [ [ 11.33 ] ] дана сводка по аксиоматическому подходу к введению метрик в пространствах нечисловой природы. К настоящему времени практически для каждой используемой в прикладных работах метрики удалось подобрать систему аксиом, из которой чисто математическими средствами можно вывести именно эту метрику.

Применения статистики объектов нечисловой природы. Идеи, подходы, результаты статистики объектов нечисловой природы оказались полезными и в классических областях прикладной статистики. Статистика в пространствах общей природы позволила с единых позиций рассмотреть всю прикладную статистику, в частности, показать, что регрессионный, дисперсионный и дискриминантный анализы являются частными случаями общей схемы регрессионного анализа в пространстве произвольной природы. Поскольку структура модели - объект нечисловой природы, то ее оценивание, в частности, оценивание степени полинома в регрессии, также относится к статистике нечисловых данных. Если учесть, что результаты измерения всегда имеют погрешности, т.е. являются не числами, а интервалами или нечеткими множествами, то приходим к необходимости пересмотреть некоторые выводы теоретической статистики. Например, отсутствует состоятельность оценок, нецелесообразно увеличивать объем выборок сверх некоторого предела (см. "Статистика интервальных данных" ).

Технико-экономическая эффективность от применения методов статистики нечисловых данных достаточно высока. К сожалению, из-за изменения экономической ситуации, в частности, из-за инфляции трудно сопоставить конкретные экономические результаты в разные моменты времени. Кроме того, методы статистики объектов нечисловой природы составляют часть методов прикладной статистики. А те, в свою очередь - часть методов, входящих в систему информационной поддержки принятия решений на предприятии. Какую часть приращения прибыли предприятия надо отнести на эту систему? Мы знаем, как работает система управления фирмой в настоящем виде. Но можем только гадать (а точнее, оценивать, скорее всего, с помощью экспертных оценок), каковы были бы результаты финансово-хозяйственной деятельности предприятия, если бы система управления фирмой была бы иной, например, не содержала методов статистики объектов нечисловой природы.

Статистика объектов нечисловой природы как часть прикладной статистики продолжает бурно развиваться. В частности, увеличивается количество ее практически полезных применений при анализе конкретных экономических данных - в маркетинговых исследованиях, контроллинге, при управлении предприятием и др.

Дальше >>

Авторизоваться

Прикладная статистика

Статистика нечисловых данных

11.1. Структура статистики нечисловых данных

Вопросы и ответы