НОУ ИНТУИТ | Прикладная статистика. Лекция 11: Статистика нечисловых данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать программу

11.5. Статистика нечетких множеств

Нечеткие множества - частный вид объектов нечисловой природы. Поэтому при обработке выборки, элементами которой являются нечеткие множества, могут быть использованы различные методы анализа статистических данных произвольной природы - расчет средних, непараметрических оценок плотности, построение диагностических правил и т.д.

Среднее значение нечеткого множества. Однако иногда используются методы, учитывающие специфику нечетких множеств. Например, пусть носителем нечеткого множества является конечная совокупность действительных чисел 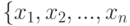$\{x_1, x_2, ..., x_n}$ . Тогда под средним значением нечеткого множества иногда понимают число. А именно, среднее значение нечеткого множества определяют по формуле:

$M(A)=\frac{\sum\limits_{i=1}^nx_i\mu_A(x_i)}{\sum\limits_{i=1}^n\mu_A(x_i)},$

где $\mu_A(x_i)$ - функция принадлежности нечеткого множества

. Если знаменатель равен 1, то эта формула определяет математическое ожидание случайной величины, для которой вероятность попасть в точку x_i

равна $\mu_A(x_i)$ . Такое определение наиболее естественно, когда нечеткое множество

интерпретируется как нечеткое число.

Очевидно, наряду с 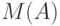M(A) может оказаться полезным использование эмпирических средних, определяемых (согласно статистике в пространствах общей природы) путем решения соответствующих оптимизационных задач. Для конкретных расчетов необходимо ввести то или иное расстояние между нечеткими множествами.

Расстояния в пространствах нечетких множеств. Как известно, многие методы статистики нечисловых данных базируются на использовании расстояний (или показателей различия) в соответствующих пространствах нечисловой природы. Расстояние между нечеткими подмножествами и множества $X = \{x_1, x_2, ..., x_k}$ можно определить как

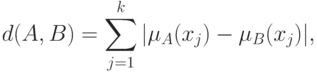
$d(A,B)=\sum_{j=1}^k|\mu_A(x_j)-\mu_B(x_j)|,$

где $\mu_A(x_j)$ - функция принадлежности нечеткого множества

, а $\mu_B(x_j)$ - функция принадлежности нечеткого множества

. Может использоваться и другое расстояние:

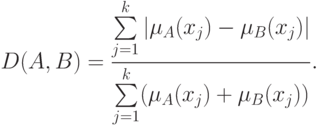
$D(A,B)=\frac{\sum\limits_{j=1}^k|\mu_A(x_j)-\mu_B(x_j)|}{\sum\limits_{j=1}^k(\mu_A(x_j)+\mu_B(x_j))}.$

(Примем это расстояние равным 0, если функции принадлежности тождественно равны 0.)

В соответствии с аксиоматическим подходом к выбору расстояний (метрик) в пространствах нечисловой природы разработан обширный набор систем аксиом, из которых выводится тот или иной вид расстояний (метрик) в конкретных пространствах, в том числе в пространствах нечетких множеств (см. "Различные виды статистических данных" ). При использовании вероятностных моделей расстояние между случайными нечеткими множествами (т.е. между случайными элементами со значениями в пространстве нечетких множеств) само является случайной величиной, имеющей в ряде постановок асимптотически нормальное распределение [ [ 1.18 ] ].

Проверка гипотез о нечетких множествах. Пусть ответ эксперта - нечеткое множество. Естественно считать, что его ответ, как показание любого средства измерения, содержит погрешности. Если есть несколько экспертов, то в качестве единой оценки (группового мнения) естественно взять эмпирическое среднее их ответов. Но возникает естественный вопрос: действительно ли все эксперты измеряют одно и то же? Может быть, глядя на реальный объект, они оценивают его с разных сторон? Например, на научную статью можно смотреть как с теоретической точки зрения, так и с прикладной, и соответствующие оценки будут скорее всего различны (если они совпадают, то работа либо никуда не годится, либо является выдающейся).

Итак, возник вопрос: как проверить согласованность мнений экспертов? Надо сначала определить понятие согласованности. Пусть - нечеткий ответ эксперта. Будем считать, что соответствующая функция принадлежности есть сумма двух слагаемых:

$\mu_A(u)-\mu_{N(A)}(u)+\xi_A(u),$

где

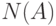- "истинное" нечеткое множество, а $\xi_A(u)$ - "погрешность" эксперта как прибора. Естественно рассмотреть две постановки.

Мнения экспертов A(1), A(2), ..., A(m) будем считать согласованными, если

Рассмотрим две группы экспертов. В первой у всех "истинное" мнение 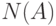N(A) , а во второй у всех - N(B) . Две группы будем считать согласованными по мнениям, если

Согласованность определена. Как же ее проверить? Если экспертов достаточно много, то эти гипотезы можно проверять отдельно для каждого элемента множества - общего носителя нечетких ответов. Проверка последней гипотезы переходит в проверку однородности двух независимых выборок ( "Статистический анализ числовых величин" ). Здесь ограничимся постановками основных гипотез (ср. с аналогичными гипотезами, рассмотренными выше для люсианов).

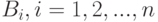Восстановление зависимости между нечеткими переменными. Рассмотрим две нечеткие переменные и . Пусть каждый из испытуемых выдает в ответ на вопрос два нечетких множества A_i и B_i, i = 1, 2, ..., n . Необходимо восстановить зависимость от , другими словами, наилучшим образом приблизить с помощью .

Для иллюстрации основной идеи ограничимся парной линейной регрессией нечетких множеств. Нечеткое множество назовем линейной функцией от нечеткого множества , если для любого из носителя функции принадлежности множеств и таковы, что $\mu_C(x) = \mu A(y)$ при $x = \alpha y + \beta$ . Другими словами,

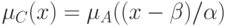
$\mu_C(x)=\mu_A((x-\beta)/\alpha)$

для любого

из носителя

. В таком случае естественно писать

$C=\alpha A + \beta.$

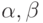Однако нечеткие переменные, как и привычные статистикам числовые переменные, обычно несколько отклоняются от линейной связи. Наилучшее линейное приближение нечеткой переменной с помощью линейной функции от нечеткой переменной естественно искать, решая задачу минимизации по $\alpha, \beta$ расстояния от до . Пусть

$\rho(B,\alpha_0 A+\beta_0)=\min\rho(B,\alpha A+\beta),$

где $\rho$ - некоторое расстояние между нечеткими множествами, а минимизация проводится по всем возможным значениям $\alpha$ и $\beta$ . Тогда наилучшей линейной аппроксимацией

является $\alpha_0 A + \beta_0$ . Если рассматриваемый минимум равен 0, то имеет место точная линейная зависимость.

Для восстановления зависимости по выборочным парам нечетких переменных естественно воспользоваться подходом, развитым в статистике в пространствах произвольной природы для параметрической регрессии (аппроксимации). В соответствии с 6.3 в качестве наилучших оценок параметров линейной зависимости следует рассматривать

$\left(\alpha^*,\beta^*\right)=Arg\min_{\alpha,\beta}\sum_{k=1}^n\rho(B_i,\alpha A_i+\beta).$

Тогда наилучшим линейным приближением является $C^* = \alpha^*A + \beta^*$ .

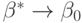Вероятностно-статистическая теория регрессионного анализа нечетких переменных строится как частный случай аналогичной теории для переменных произвольной природы (см.6.3). В частности, при обычных предположениях оценки $\alpha^*, \beta^*$ являются состоятельными, т.е. $\alpha^* \rightarrow \alpha_0$ и $\beta^* \rightarrow \beta_0$ при $n\rightarrow\infty$ .

Кластер-анализ нечетких переменных. Строить группы сходных между собой нечетких переменных (кластеры) можно многими способами. Опишем два семейства алгоритмов.

Пусть на пространстве, в котором лежат результаты наблюдений, т.е. на пространстве нечетких множеств, заданы две меры близости $\rho$ и $\tau$ (например, это могут быть введенные выше расстояния и ). Берется один из результатов наблюдений (нечеткое множество) и вокруг него описывается шар радиуса , определяемый мерой близости $\rho$ . (Напомним, что шаром с центром в относительно $\rho$ называется множество всех элементов рассматриваемого пространства таких, что $\rho(x, y) \le R$ .) Берутся результаты наблюдений (элементы выборки), попавшие в этот шар, и находится их эмпирическое среднее относительно второй меры близости $\tau$ . Оно берется за новый центр, вокруг которого снова описывается шар радиуса относительно $\rho$ , и процедура повторяется. (Чтобы алгоритм был полностью определен, необходимо сформулировать правило выбора элемента эмпирического среднего в качестве нового центра, если эмпирическое среднее состоит более чем из одного элемента.)

Когда центр шара зафиксируется (перестанет меняться), попавшие в этот шар элементы объявляются первым кластером и исключаются из дальнейшего рассмотрения. Алгоритм применяется к совокупности оставшихся результатов наблюдений, выделяет из нее второй кластер и т.д.

Всегда ли центр шара остановится? При реальных расчетах в течение многих лет так было всегда. Соответствующая теория была построена в 1977 г. [ ]. Было доказано, что описанный выше процесс всегда остановится через конечное число шагов. Причем число шагов до остановки оценивается через максимально возможное число результатов наблюдений в шаре радиуса относительно $\rho$ .

Обширное семейство образуют алгоритмы кластер-анализа типа "Дендрограмма", известные также под названием "агломеративные иерархические алгоритмы средней связи". На первом шагу алгоритма из этого семейства каждый результат наблюдения рассматривается как отдельный кластер. Далее на каждом шагу происходит объединение двух самых близких кластеров. Название "Дендрограмма" объясняется тем, что результат работы алгоритма обычно представляется в виде дерева. Каждая его ветвь соответствует кластеру, появляющемуся на каком-либо шагу работы алгоритма. Слияние ветвей соответствует объединению кластеров, а ствол - заключительному шагу, когда все наблюдения оказываются объединенными в один кластер.

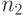Для работы алгоритмов кластер-анализа типа "Дендрограмма" необходимо определить расстояние между кластерами. Естественно использовать ассоциативные средние, которыми, как известно, являются обобщенные средние по Колмогорову всевозможных попарных расстояний между элементами двух рассматриваемых кластеров. Итак, расстояние между кластерами и , состоящими из n_1 и n_2 элементов соответственно, определяется по формуле:

$\tau(K,L)=F^{-1}\left(\frac{1}{n_1n_2}\sum_{i\in K}\sum_{j\in L}F(\rho(X_i,X_j))\right),$

где $\rho$ - некоторое расстояние между нечеткими множествами,

- строго монотонная функция (строго возрастающая или строго убывающая).

Соображения теории измерений позволяют ограничить круг возможных алгоритмов типа "Дендрограмма". Естественно принять, что единица измерения расстояния выбрана произвольно. Тогда согласно результатам $\S$ 5.3 из всех обобщенных средних по Колмогорову годятся только степенные средние, т.е. $F(z) = z^{\lambda}$ при $\lambda\ne 0$ или $F(z) = \ln z$ . Чтобы получить разбиение на кластеры, надо "разрезать" дерево на определенной высоте, т.е. объединять кластеры лишь до тех пор, пока расстояние между ними меньше заранее выбранной константы. При альтернативном подходе заранее фиксируется число кластеров. Рассматривают и двухкритериальную постановку, когда минимизируют сумму (или максимум) внутрикластерных разбросов и число кластеров. Для решения задачи двухкритериальной минимизации либо один из критериев заменяют на ограничение, либо два критерия "свертывают" в один, либо применяют иные подходы (последовательная оптимизация, построение поверхности Парето и др.).

При классификации нечетких множеств полезны многие подходы, рассмотренные в "Многомерный статистический анализ" , а именно, все подходы, основанные только на использовании расстояний.

Сбор и описание нечетких данных. Разработано большое количество процедур описания нечеткости. Так, согласно Э.Борелю понятие "куча" описывается с помощью функции распределения - при каждом конкретном значение функции принадлежности - это доля людей, считающих совокупность зерен кучей. Результат подобного опроса может дать и кривую иного вида, например, по поводу понятия "молодой" (слева будут отделены "дети", а справа - "люди зрелого и пожилого возраста"). Нечеткая толерантность может оцениваться с помощью случайных толерантностей (см. выше).

Целесообразно попытаться выделить наиболее практически полезные простые формы функций принадлежности. Видимо, наиболее простой является "ступенька" - внутри некоторого интервала функция принадлежности равна 1, а вне этого интервала равна 0. Это - простейший способ "размывания" числа путем замены его интервалом. Нечеткое множество описывается двумя числами - концами интервала. Оценки этих чисел можно получить с помощью экспертов. Статистическая теория подобных нечетких множеств рассмотрена в "Статистика интервальных данных" .

Тремя числами a < b < c описывается функция принадлежности типа треугольника. При этом левее и правее с функция принадлежности равна 0. В точке функция принадлежности принимает значение 1. На отрезке [a; b] функция принадлежности линейно растет от 0 до 1, а на отрезке [b;c] - линейно убывает от 1 до 0. Оценки трех чисел a < b < c получают при опросе экспертов.

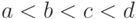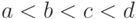Следующий по сложности вид функции принадлежности - типа трапеции - описывается четырьмя числами a < b < c < d . Левее и правее функция принадлежности равна 0. На отрезке [a; b] она линейно возрастает от 0 до 1, на отрезке [b; c] во всех точках равна 1, а на отрезке [c; d] линейно убывает от 1 до 0. Для оценивания четверки чисел a < b < c < d используют экспертов.

Ряд результатов статистики нечетких данных приведен в первой монографии российского автора по нечетким множествам [ [ 1.16 ] ] и во многих дальнейших публикациях.

Дальше >>

Авторизоваться

Прикладная статистика

Статистика нечисловых данных

11.5. Статистика нечетких множеств

Вопросы и ответы