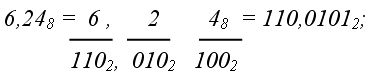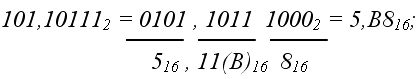|
Здравствуйте,ясдавала 15 тестов и экзамен. Мне нужно сейчас посмотреть результаты тестов.Как это сдлеать? |
Системы счисления и действия в них
Алфавит Х из р символов и правила записи (изображения) и обработки чисел с помощью символов этого алфавита называются системой счисления (нумерацией) с основанием р. Число х в системе с основанием р обозначается как (х)р или хр .
Любая система счисления – это система кодирования числовых величин (количеств), позволяющая выполнять операции кодирования и декодирования, то есть по любой количественной величине однозначно находить его кодовое представление и по любой кодовой записи – восстанавливать соответствующую ей числовую величину.
Все системы счисления строятся по общему принципу: определяется величина р – основание системы, а любое число х записывается в виде комбинации степеней веса р от 0-й до n-й степени следующим образом:
(x)10 = xnpn + xn–1pn–1 + ... + x1p1 + x0p0 .
Наиболее используемые в информатике системы счисления, кроме, естественно, десятичной, – это: 1) двоичная, над алфавитом Х = {0,1} ; 2) восьмеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7} ; 3) шестнадцатеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F}, где символы А, В, С, D, Е, F имеют, соответственно, десятичные веса 10, 11, 12, 13, 14, 15.
Пример. 11012 = 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 8 + 4 + 1 = 1310 ,
1578 = 1 x 82 + 5 x 81 + 7 x 80 = 64 + 40 + 7 = 11110 ,
A6F16 = 10 x 256 + 6 x 16 + 15 x 1 = 267110 .
В большинстве систем счисления вес цифры (или символа алфавита) зависит от ее места в записи числа или слова. Такая система счисления называется позиционной ; в противном случае система называется непозиционной.
Пример. Непозиционная система – древняя римская система записи чисел с алфавитом вида Х={I (1), V (5), Х (10), L (50), С (100), D (500), М (1000)}, где в скобках указаны веса символов (не зависящие от позиции символа). Примеры римских чисел (в скобках – обычные десятичные эквиваленты): III (3), IV (4), V (5), VI (6), IX (9), XI (11), DCL (650). Запись числа в этой системе получается двусторонней конкатенацией, причем правая конкатенация ассоциируется с добавлением, а левая конкатенация – с убавлением (например, IV и VI ). Поразрядное же выполнение арифметических операций не имеет места (например, XIV + IV = XVIII ).
Для изображения десятичных дробей используется подобная формула разложения по степеням основания.
Пример. 110,0012 = 1x22 + 1 x 21 + 0 x 20 + 0 x 2-1 + 0 x 2-2 + 1 x 2-3 = 6,12510 ;
A,B16 = A x 160 + B x 16-1 = 10 x 1 + 11 x 0,0625 = 10,687510 .
Процедура перевода десятичных чисел в р-ную систему счисления:
- перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]10 , а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р ; изображение [х]p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого;
- перевести отдельно дробную часть (мантиссу) числа, то есть {x}10 , для чего последовательно умножать сперва исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}p ; изображение {х}p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части;
- результат будет иметь вид (х)р = [х]p, {х}p .
Пример. Найти: 12,810 = ?2 . Решение:
- Переводим целую часть: 1210 =11002;
- переводим дробную часть: 0,8 x 2 = 1,6; 0,6 x 2 = 1,2; 0,2 x 2 = 0,4; 0,4 x 2 = 0,8; 0,810 = 0,1100110...2 ;
- результат перевода: 12,810 = 1100,1100110011...2 .
Пример. Найдем 29,2510 = ?8 . Решение имеет вид 1) 2910 = 358 ; 2) 0,2510 = 0,28 ; 3) 29,2510 = 35,28 .
Пример. Найдем 79,2610 = ?16 . Решение: 1) 7910 = 4F16 ; 2) 0,2610 = 0,4016 ; 3) 79,2610 = 4F,416 . При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно.
Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида:
| 10 | 2 | 8 | 16 |
|---|---|---|---|
| 0 | 0 | 000 | 0000 |
| 1 | 1 | 001 | 0001 |
| 2 | — | 010 | 0010 |
| 3 | — | 011 | 0011 |
| 4 | — | 100 | 0100 |
| 5 | — | 101 | 0101 |
| 6 | — | 110 | 0110 |
| 7 | — | 111 | 0111 |
| 8 | — | — | 1000 |
| 9 | — | — | 1001 |
| 10 | — | — | 1010 |
| 11 | — | — | 1011 |
| 12 | — | — | 1100 |
| 13 | — | — | 1101 |
| 14 | — | — | 1110 |
| 15 | — | — | 1111 |
При переводе в 8-ную систему или из нее необходимо группировать в тройки биты, а при переводе в 16-ную или из нее – группировать их в четверки битов. Можно добавлять, если нужно, незначащие нули (слева от целой части и справа от мантиссы) или отбрасывать их.
Пример. Рассмотрим переводы в смешанных системах.
-
Из 2-ной системы в 8-ную (двоично-восьмеричное изображение):
-
из 8-ной системы в 2–ную (восьмерично-двоичное изображение):
-
из 2-ной системы в 16-ную (двоично-шестнадцатеричное изображение):
-
из 16-ной системы в 2-ную (шестнадцатерично-двоичное изображение):
Сложение в двоичной системе счисления осуществляется по правилам
0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 210 = 102 (единица идет в старший разряд).
Таблица вычитания в двоичной системе счисления имеет вид
0 – 0 = 0, 1 – 0 = 1, 1 – 1 = 0, 0 – 1 = 10 – 1 = 1 (единицу забираем у старшего разряда).
Таблица умножения в двоичной системе счисления имеет вид
0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1.
Таблица деления в двоичной системе счисления имеет вид
0 : 0 = не определено, 1 : 0 = не определено, 0 : 1 = 0, 1 : 1 = 1.