НОУ ИНТУИТ | Разработка телетрафика и планирование сетей. Лекция 15: Сети очередей

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 20.04.2011 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать программу

Другие алгоритмы для сетей очередей

MVA -алгоритм также применим к сетям очередей с большим количеством цепочек, но это не будет описано здесь. В течение прошлого десятилетия были разработаны несколько алгоритмов. Их краткий обзор приводится в (Conway и Georganas, 1989 [15]). Вообще, для больших сетей точные алгоритмы не применимы. Поэтому, чтобы иметь дело с сетями очередей реального размера, было разработано много приблизительных алгоритмов.

Сложность

Сети очередей имеют такую же сложность, что и сети с коммутацией каналов и прямой маршрутизацией (секция 11.5 и табл. 11.2). Пространство состояний сети, показанной в таблице 14.3, имеет следующее число состояния для каждого узла:

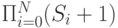$\Pi_{i=0}^N(S_i+1)$

( 14.20)

Худший случай - тот, когда каждая цепочка состоит из одного клиента. Тогда число состояний становится 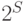2^S , где - число клиентов.

Таблица 14.3. Параметры сети организации очереди с цепочками, узлами и $\sum_iS_i$ клиентами. Параметр $\alpha_{jk}$ обозначает нагрузку от клиентов цепочки в узле (см. Табл. 11.2).
Цепочка	Узел $\begin{matrix}1&2&\dots & K \end{matrix}$	Число клиентов
1	$\begin{matrix} \alpha_{11}& \alpha_{21} &\dots & \alpha_{K1} \end{matrix}$
2	$\begin{matrix} \alpha_{12} & \alpha_{22} &\dots & \alpha_{K2} \end{matrix}$
$\dots$	$\dots$	$\dots$
	$\begin{matrix} \alpha_{1N} & \alpha_{2N} &\dots & \alpha_{KN} \end{matrix}$

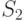Оптимальное распределение производительности

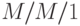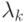Рассмотрим систему передачи данных с узлами, которые являются независимыми узлами системы организации очереди с одним обслуживающим прибором M/M/1 (Эрланговская система с ожиданием с одним обслуживающим прибором). Процесс поступления вызовов к узлу - Пуассоновский процесс с интенсивностью $\lambda_k$ сообщений (клиентов) в единицу времени. Размер сообщения - экспоненциально распределенное значение со средней величиной 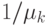$1/\mu_k$ [бит]. Пропускная способность узла - равна $\varphi_k$ [бит в единицу времени]. Среднее время обслуживания равно:

$s=\frac{1/\mu_k}{\varphi_k}=\frac{1}{\mu_k \varphi_k}$

Так что средняя скорость обслуживания - $\mu_k * \varphi_k,$ а среднее время пребывания определяется (12.34):

$m_{1,k}=\frac{1}{\mu_k \varphi_k - \lambda_k}$

Вводим следующее линейное ограничение на полную производительность:

$F=\sum_{k=1}^K \varphi_k$

( 14.21)

Для каждого распределения производительности, которая удовлетворяет (14.21), получаем следующее среднее время пребывания для всех сообщений (математическое ожидание вызова):

$m_1=\sum_{k=1}^K \frac{\lambda_k}{\lambda}*\frac{1}{\mu_k* \varphi_k - \lambda_k}$

( 14.22)

где

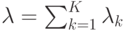$\lambda=\sum_{k=1}^K \lambda_k$

( 14.23)

Применяя (13.14), получаем полное среднее время обслуживания:

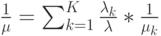$\frac{1}{\mu}=\sum_{k=1}^K \frac{\lambda_k}{\lambda}*\frac{1}{\mu_k}$

( 14.24)

Полная предложенная нагрузка тогда:

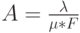$A=\frac{\lambda}{\mu*F}$

( 14.25)

Закон Клейнрока для оптимального распределения производительности (Kleinrock, 1964 [65]) сформулирован следующим образом.

Теорема 14.2. Закон квадратного корня Закон квадратного корня (закон Клейнрока): оптимальное распределение производительности ( $\varphi_k$ ), которое минимизирует m_1 (и таким образом общее количество сообщений во всех узлах):

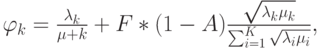$\varphi_k=\frac{\lambda_k}{\mu+k}+F*(1-A)\frac{\sqrt{\lambda_k \mu_k}}{\sum_{i=1}^K \sqrt{\lambda_i \mu_i}},$

( 14.26)

при условии, что:

$F > \sum_{k=1}^K \frac{\lambda_k}{\mu_k}$

( 14.27)

Доказательство. Вводя множитель 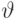$\vartheta$ Лагранжа и рассматривая:

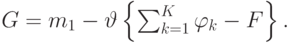$G=m_1- \vartheta \left \{ \sum_{k=1}^K \varphi_k -F \right \}.$

( 14.28)

Минимум получен, если выбирать $\varphi_k,$ как приведено в (14.26). С этим оптимальным распределением находим среднее время пребывания:

$m_1=\frac{\left \{\sum_{k=1}^K \sqrt{\lambda_k/ \mu_k} \right \}^2}{\lambda*F*(1-A)}$

( 14.29)

Это оптимальное распределение соответствует тому случаю, когда необходимая минимальная производительность $\lambda_k/ \mu_j$ сначала распределена между всеми узлами. Остающаяся производительность (14.24):

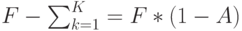$F-\sum_{k=1}^K=F*(1-A)$

( 14.30)

Данная производительность распределена между узлами пропорционально квадратному корню из среднего потока $\lambda_k/ \mu_k$ .

Если все сообщения имеют одинаковую среднюю величину $(\mu_k= \mu)$ то мы можем рассчитать различные затраты в узлах, согласно ограничению, которое фиксирует количество доступных узлов (Kleinrock,1964 [65]).

Краткие итоги

Многие системы могут быть представлены как сеть, в которой клиент получает доступ к услуге через нескольких последовательных узлов, обслуживается только одним узлом и далее сразу продолжает обслуживание на другом узле.
Система - сеть очередей - это сеть организации очередей, где каждая отдельная очередь является узлом. Примеры сетей очередей - телекоммуникационные системы, компьютерные системы, сети пакетной коммутации.
В сетях очередей мы определяем длину очереди на данном узле как общее количество клиентов в этом узле, включая обслуживаемых клиентов.
Сети очередей разделяются на закрытые и открытые сети. В закрытых сетях очередей число клиентов постоянно, тогда как в открытых сетях очередей число клиентов изменяется.
Состояние сети очередей определяется как одновременное распределение числа клиентов на каждом узле. Если K обозначает общее количество узлов, то состояние отображается вектором
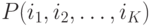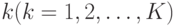$P(i_1, i_2, \dots, i_K)$ , где - число клиентов на узле $k (k = 1, 2, \dots, K)$ .
Пространство состояний является очень большим, и, решая уравнения равновесия узла, трудно вычислить вероятности состояния. Вероятности состояния сетей с мультипликативной формой могут быть объединены и получены, используя алгоритм свертывания (секция 14.4.1) с помощью MVA - алгоритма.
Сети очередей могут быть обобщены, если есть типов клиентов. Клиенты одного заданного типа принадлежат так называемой цепочке.
Четыре модели организации очереди обладают свойством, при котором процесс выхода из системы организации очереди - Пуассоновский процесс: $M/M/n, M/G/ \infty , M/G/1-PS, M/G/1-LCFS-PR$ .
Джексон показал, что -узлы сети очередей имеют мультипликативную форму. Ключевая точка теоремы Джексона: каждый узел можно рассматривать независимо от всех других узлов и вероятности состояний можно определить, используя C-формулу Эрланга.
При обслуживании заявок клиентов на сетях очередей часто будет возникать "зацикливание", когда заявка клиента посещает один и тот же узел несколько раз. Если мы имеем сеть очередей с заявками зацикливания, где узлы - системы , то процессы поступления вызовов к отдельным узлам не будут Пуассоновскими процессами.
В сети с информацией обратной связи процесс поступления вызовов будет взрывной. То есть когда имеется один (или больше) клиентов в системе, интенсивность поступления к каждому узлу будет относительно высока, тогда как если нет никаких клиентов в системе, то интенсивность поступления будет очень низка.
В случае взрывного процесса, вместо того, чтобы рассматривать единственное экспоненциальное распределение интервала, мы можем анализировать фаз и рассматривать каждую фазу как поступление.
Теория сети очередей принимает, что пакет (клиент) производит выбор нового времени обслуживания на каждом узле. Это необходимое предположение для мультипликативной формы.
Расчет открытых систем прост. Сначала мы получаем объединенную интенсивность прибытия к каждому узлу ( 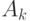), далее получаем предложенную нагрузку 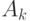на каждом узле, затем, рассматривая Эрланговскую систему с ожиданием, получаем вероятности состояния для каждого узла.
Исследование закрытых сетей с очередями намного сложнее, чем открытых. Мы можем получить относительную нормализованную вероятность состояния. Наконец, нормализуя, мы получим нормализованные вероятности состояния.
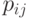Сети очередей с более чем одним типом клиентов также имеют мультипликативную форму, при условии, что каждый узел имеет симметричную систему организации очереди и клиенты классифицированы в цепочки. Каждая цепочка характеризуется своим собственным средним временем обслуживания и вероятностями перехода $p_{ij}$ (BCMP-сети).
Многомерные сети организации очереди - это сети очередей с более чем одним типом клиентов. Клиенты одного и того же типа принадлежат заданному классу или цепочке.
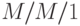-система организации очереди с одним обслуживающим прибором при одной из интерпретаций может рассматриваться как система совместного использования процессора. То есть все , клиентов совместно используют обслуживающий прибор, а производительность сервера является постоянной.
Системы организации очереди c одним обслуживающим прибором и большим количеством типов клиентов будут иметь мультипликативную форму только тогда, когда узел имеет симметричную систему организации очереди: или 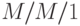с одинаковым временем обслуживания для всех клиентов.
система организации очереди при $(i + j) \le n$ может быть рассчитана с помощью B-формулы Эрланга. При 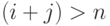решение может быть получено только для простого случая, когда 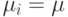$\mu_i= \mu$ то есть когда все типы (цепочки) клиентов имеют одинаковое среднее время пребывания в системе.
Рассмотрение сетей очередей, имеющих много цепочек, аналогично случаю с единственной цепочкой. Основное различие состоит в том, что классическая формула и алгоритмы заменены соответствующей многомерной формулой. Алгоритм по существу применяется такой же, как и в случае единственной цепочки.
Закон квадратного корня (закон Клейнрока): оптимальное распределение производительности (, которое минимизирует m1 (и таким образом общее количество сообщений во всех узлах):

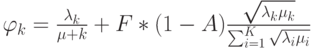$\varphi_k=\frac{\lambda_k}{\mu+k}+F*(1-A)\frac{\sqrt{\lambda_k \mu_k}}{\sum_{i=1}^K \sqrt{\lambda_i \mu_i}}$ ,