НОУ ИНТУИТ | Разработка телетрафика и планирование сетей. Лекция 10: Теория перегрузки

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 20.04.2011 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать программу

Разбиение нагрузки

Здесь мы дадим естественную интерпретацию метода Фредерикса и Хэйварда, и в то же самое время обсудим разбиение потоков нагрузки. Рассмотрим поток нагрузки со средней величиной А, дисперсией v, и пиковостью Z= v/A. Разобьем этот поток нагрузки на g идентичных под-потоков. Один из таких подпотоков тогда имеет среднюю величину A/g и пиковость Z/g, потому что средняя величина уменьшена на коэффициент g, а дисперсия на коэффициент 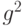g^2 (Пример 3.3.2). Если мы выбираем число g подпотоков, равное Z, то получаем пиковость Z= 1 для каждого подпотока.

Предположим, что первоначальный поток нагрузки поступает на п каналов. Если мы разбиваем п каналов на g подгрупп (одну для каждого подпотока), то каждая подгруппа содержит n/g каналов.

Каждая подгруппа будет тогда иметь такую же вероятность блокировки, как первоначальная полная система. Выбирая g=Z, мы получаем пиковость Z=1 в подпотоках и можем (приблизительно) использовать В-формулу Эрланга для того, чтобы вычислить вероятность блокировки.

Это естественная интерпретация метода Хэйварда и Фредерикса. Она может легко быть расширена, чтобы включить мультислотовую нагрузку. Если каждый вызов требует d каналов в течение всего времени соединения то, разбивая нагрузку на d подпотоков, получим систему, где каждый вызов будет использовать единственный канал в каждой из подгрупп d. Тогда мы получим d идентичных системы с нагрузкой одного-единственного слота.

Вышеупомянутое разбиение нагрузки на g идентичных потоков нагрузки показывает, что вероятность блокировки, полученная методом Фредерикса-Хэйварда - потери по нагрузке. Равное разбиение нагрузки в любой момент времени подразумевает, что все потоки нагрузки g идентичны и таким образом имеют взаимную корреляцию, равную единице. В действительности, мы не можем разбить нагрузку коммутации каналов на идентичные подпотоки. Если мы имеем потоки g=2, и три канала заняты в данный момент времени, то можно, например, использовать два канала в одном подпотоке и один в другом. Но, так или иначе, мы получаем то же самое оптимальное использование как в полной системе, потому что всегда будем иметь доступ к свободному каналу в любой подгруппе (полная доступность). Корреляция между подпотоками становится меньше, чем единица. Вышеупомянутое положение является примером использования интеллектуальных стратегий для поддержки оптимальной полной доступности.

В секции 6.3.2 мы изучили разбиение процесса поступления вызовов, когда разбиение сделано случайным способом (Теорема Райкова 6.2). Этим разбиением не уменьшается отклонение процесса для случаев, когда процесс - Пуассоновский процесс или более регулярный. В результате процессы подпотока сходятся к Пуассоновским процессам. В этой мы рассмотрим разбиение процесса нагрузки, который включает и процесс поступления вызовов, и времена пребывания в системе. Процесс разбиения зависит от состояния. Большое время пребывания в системе единственного вызова приведет к нескольким новым вызовам в этом подпроцессе в течение следующего временного интервала, и процесс поступления вызовов больше не будет процессом рождения.

Большинство попыток улучшения и метода эквивалентности Фредерикса-Хэйварда основаны на сокращении корреляции между подпотоками, потому что процессы поступления вызовов для одного подпотока рассматриваются как процессы рождения, а времена пребывания в системе предполагаются экспоненциально распределенными. Из вышеупомянутых положений ясно, что рассмотренные подходы являются неудачными, потому что они не приводят к оптимальному разбиению нагрузки. В следующем примере мы убедимся, что оптимальное разбиение может быть реализовано для пакетов обслуживания нагрузки с постоянным размером пакета.

Если мы разбиваем поток нагрузки на подпотоки так, чтобы занятый канал принадлежал подпотоку с вероятностью р, то можно показать, что подпотоку присваивается пиковость 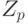Z_p :

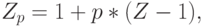
где Z - пиковость из первоначального потока. Из этого случайного разбиения нагрузки мы видим, что пиковость сходится к единице при уменьшении р. Это соответствует Пуассоновскому процессу, и такой результат справедлив для любого процесса нагрузки.

Пример 9.3.3: Обратное мультиплексирование

Если необходима большая пропускная способность сети, чем предоставляет одиночный канал, то мы можем параллельно комбинировать больше каналов. В первоначальном источнике можно распределить нагрузку (пакеты или ячейки в ATM) циклическим способом по отдельным каналам, и в пункте назначения восстановить первоначальную информацию. Этим способом мы достигаем более высокую пропускную способность, арендуя очень дорогие широкополосные каналы. Если нагрузки содержит пакеты постоянного размера, то процесс передачи нагрузки можно разбить на множество идентичных потоков нагрузки и получить такое же использование, как в отдельной системе с полной емкостью. Этот принцип сначала эксплуатировался на датских сетях (Johansen и Johansen и Rasmussen, 1991 [53]), где была возможность комбинировать до 30 индивидуальных каналов цифровой сети интегрального обслуживания со скоростью 64 Кбит/с для передачи видеонагрузки при обслуживании самолетов.

Сегодня подобное оборудование применяется для того, чтобы объединить множество каналов со скоростью 2 Мбит/с, которые используются подключениями ATM с большей пропускной способностью. Этот метод называется Инверсное Мультиплексирование для ATM (IMA Inverse Multiplexing for ATM) (Techguide, 2001 [96]), (Postigo Boix и Garcia-Haro и Aguilar-Igartua, 2001 [83]).

Другие методы, основанные на пространстве состояний

С точки зрения блокировки, средняя величина и дисперсия не обязательно характеризуют нагрузку оптимальным способом. Другие параметры могут лучше описать нагрузку. При вычислении ERТ методом блокировки мы имеем два уравнения с двумя неизвестными (9.6 и 9.7). Система с потерями Эрланга однозначно определяется числом каналов и предложенной нагрузки 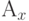А_x . Поэтому невозможно обобщить метод, принимая во внимание только два момента (среднее значение и дисперсию).

ВРР-модели нагрузки

ВРР -модели нагрузки описывают нагрузку двумя параметрами, средней величиной и пиковостью, и поэтому являются естественными кандидатами для моделирования нагрузки двумя параметрами.

Тем не менее, исторически концепция и определение потерь по нагрузке имеют более ранние модели, исходящие из предложенной нагрузки, которые приводят к путанице, поскольку определяют потери по вызовам. Как отмечалось на рис. 8.6, для вычислений перегрузки имеют смысл только потери по нагрузке.

BРР -модель очень хорошо применима ко многим приложениям определения потерь по нагрузке.

Пример 9.4.1: ВРР-модель нагрузки

Если мы применяем ВРР -модель к нагрузке перегрузки в примере 9.2.3, то получим А = 6,6095 и Z = 1,.4038. Это соответствует нагрузке Паскаля от S= 16,37 источников и 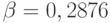$\beta = 0,2876$ . Потери по нагрузке равны 20,52 %, что соответствует потерянной нагрузке 1,3563 Эрл., тогда вероятности блокировки для системы равняются Е= 1,3563/24 = 5.65 %. Этот результат дает достаточную точность.

Метод Сандера

Sanders и Haemers и Wilcke (1983 [23]) предложили другой простой и интересный метод эквивалентности, который также базировался на пространстве состояний. Мы называем его методом Сандера. Подобно методу Фредерикса и Хэйварда, он основан на преобразовании вероятностей состояния так, чтобы пиковость стала равной единице. Метод преобразовывает не Пуассоновскую нагрузку (среднее значение, дисперсия) = (т, v) в нагрузку потока с пиковостью единица, прибавляя к нему постоянный поток (нулевая дисперсия) нагрузки со средним значением v - т так, чтобы полная нагрузка имела среднее значение, равное дисперсии v. Постоянный поток нагрузки занимает непрерывно v-т каналов (без потерь), и этим мы увеличиваем число каналов. Таким способом мы получаем систему с п + (v-m) каналами, на которые поступает нагрузка т + (v - т) = v Эрл. Пиковость становится единицей, и вероятность блокир овки может быть получена по В-формуле Эрланга, так что мы находим нагрузку, потерянную от эквивалентной системы. Эта потерянная нагрузка делится на первоначальную и предложенную нагрузку, чтобы получить потери по нагрузке С.

Вероятность блокировки касается первоначально предложенной нагрузки т. Метод применим для гладкой т > v и взрывной нагрузки т < v и требует только оценки по В-формуле Эрланга с непрерывным числом каналов.

Пример 9.4.2: метод Сандера

Если мы применяем метод Сандера к примеру 9.2.3, то увеличиваем и число каналов, и предложенную нагрузку v - m = 2,6691 (каналов/Эрл.) и таким образом имеем 9,2786 Эрл, поступающие на 10,6691 каналов. Из В-формулы Эрланга находим потерянную нагрузку 1,3690 Эрл, что является приблизительным значением, но близко к результатам, полученным выше. Это соответствует вероятности блокировки Е = 1,3690/24 = 5.70 %.

Метод Беркли

Полученный ERT -метод базировался только на одном параметре, и можно, в принципе, сохранить п произвольным или фиксированным. Опыт показывает, что лучшие результаты получаются, если сохранить число каналов 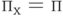п_х = п . Мы находимся теперь в положении, когда можем только гарантировать, что средняя величина нагрузки перегрузки правильна. Этот метод назван методом эквивалентности Беркли (1934). Метод Уилкинсона-Бретшнайдера (Wilkinson-Bretschneider's) требует некоторого количества вычислений (компьютерных), тогда как метод Беркли основан исключительно на В-формуле Эрланга. Метод Беркли применим лишь для систем, где первичные группы имеют одинаковое число каналов.

Пример 9.4.3: Разделение группы на первичную группу и группу перегрузки

Если мы применяем метод Беркли для примера 9.1.1, то получаем точное решение, и этот специальный случай порождает идею этого метода.

Пример 9.4.4: Метод Беркли

Снова рассматриваем пример 9.2.3. Чтобы применить правильно метод Беркли, мы должны иметь одинаковое число каналов во всех трех микроячейках. Предположим, что все микроячейки имеют 8 каналов (а не 16, 8, 0, соответственно). Чтобы получить нагрузку перегрузки 6,6095Эрл, эквивалентная предложенная нагрузка должна быть 13,72 Эрл на 8 первичных каналов. Эквивалентная система тогда имеет нагрузку 13,72 Эрл, поступающую на (8+8) = 16 каналов. Потерянная нагрузка, полученная из В-формулы Эрланга, равна 1,4588 Эрл, при вероятности блокировки 6,08 %. Это значение немного больше, чем правильное значение. Метод Беркли дает надежные результаты.

Методы, основанные на процессах поступления вызовов

Все модели в Лекциях 7 и 8 использовали Пуассоновские потоки вызовов с интенсивностью, которая зависит от состояния, тогда как времена обслуживания являются экспоненциально распределенными с равной средней величиной для всех однородных приборов обслуживания. Все эти модели независимы от распределения времени обслуживания (то есть нечувствительны к значению вероятностей состояний, и зависят только от средней величины распределения времени обслуживания). Тогда мы можем обобщить модели, рассматривая больше общих процессов поступления вызовов. При использовании общих процессов поступления вызовов свойство независимости от распределения времени потеряно, и распределение времени обслуживания становится важным параметром. Если мы имеем только один процесс поступления вызовов и много процессов обслуживания (один для каждого из п обслуживающих приборов), тогда можно предположить, что время обслуживания экспоненциальное для того, чтобы избежать сложных моделей.

Прерывистый Пуассоновский процесс

В секции 6.4 мы рассматривали прерывистый Пуассоновский процесс Качуры ( IPP ) (Kuczura, 1977 [71]), который характеризуется тремя параметрами и широко используется для моделирования нагрузки перегрузки. Возьмем полнодоступную группу с п обслуживающими приборами, на которые поступают вызовы, прибывающие согласно IPP (см. рис.6.7) с экспоненциально распределенными временами обслуживания.

Тогда мы можем создать диаграмму переходов состояний, как показано на рис.9.6. Диаграмма двухмерная. Состояние (i, j) обозначает, что есть i обслуживаемых вызовов (i = 0,1,..., n) , а процесс поступления вызовов находится в фазе j ( j = а, если идет процесс поступления вызовов, и j = b, если процесс возвращает вызов). Используя уравнения равновесия узлов, находим вероятности состояния равновесия p(i,j) .

Потери по времени E равны:

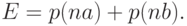( 9.20)

Потери по вызовам В равны:

$B=\frac{p(na)}{\sum_{i=0}^np(ia)} \ge E.$

( 9.21)

Потери по нагрузке С определяются как соотношение предложенной нагрузки и потерянной нагрузки. Предложенная нагрузка равна:

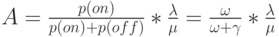$A=\frac{p(on)}{p(on)+p(off)}*\frac{\lambda}{\mu}=\frac{\omega}{\omega+ \gamma}*\frac{\lambda}{\mu}$

( 9.22)

Обслуженная нагрузка:

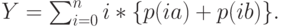
$Y=\sum_{i=0}^n i*\{p(ia)+p(ib)\}.$

Из этого уравнения мы получаем С=(А- Y)/A. Фактически, потери по нагрузке будут равны потерям по вызовам, так как процесс поступления вызовов является процессом рождения. Но это трудно вывести из полученных выше результатов. Как показано в секции 6.4.1, интервалы поступления распределены по гиперэкспоненте Н2.

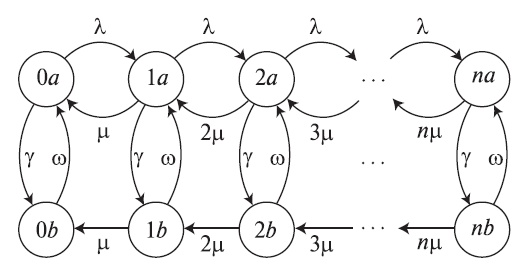
Диаграмма переходов состояний для полнодоступной системы с потерями с п обслуживающими приборами, IPP-процессом поступления вызовов (см. рис.6.7) и экспоненциально распределенным временем обслуживания.

Рис. 9.6. Диаграмма переходов состояний для полнодоступной системы с потерями с п обслуживающими приборами, IPP-процессом поступления вызовов (см. рис.6.7) и экспоненциально распределенным временем обслуживания.

Процесс поступления вызовов Кокс-2

В секции 6.4 мы отмечали, что процесс поступления вызовов Кокс-2 дает более общее представление процесса, чем IPP (Kuczura, 1977 [71]). Если мы рассматриваем процесс поступления вызовов Кокс-2, как показано на рис.4.10, то получаем диаграмму переходов состояний на рис.9.7. Из неё мы находим, согласно предположению о статистическом равновесии вероятности состояния, следующие критерии качества работы:

Потери по времени Е:

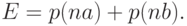( 9.23)

Потери по вызовам В:

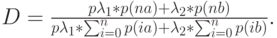$D=\frac{p \lambda_1*p(na)+ \lambda_2*p(nb)}{p \lambda_1*\sum_{i=0}^n p(ia)+ \lambda_2*\sum_{i=0}^n p(ib)}.$

( 9.24)

Потери по нагрузке С. Предложенная нагрузка это среднее число среднего времени обслуживания, деленная на число попыток вызова. Средний интервал поступления:

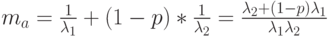
$m_a=\frac{1}{\lambda_1}+(1-p)*\frac{1}{\lambda_2}=\frac{\lambda_2+(1-p) \lambda_1}{\lambda_1 \lambda_2}$

Предложенная нагрузка тогда равна 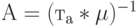$А = (т_а * \mu)^{-1}$ Обслуженная нагрузка определяется по (9.22) с помощью рис.9.7, и таким образом мы находим потери по нагрузке С.

Если мы обобщим процесс поступления вызовов на процесс поступления вызовов Кокс-k, то диаграмма перехода состояний будет все еще двухмерной. При использовании распределения Кокса мы можем в принципе рассматривать любое число параметров.

Если мы обобщаем время обслуживания с использованием распределения Кокса- k, то диаграмма переходов состояний для n > 1 становится намного более сложной, потому что существует процесс обслуживания для каждого обслуживающего прибора, но только один процесс поступления вызовов. Поэтому мы всегда обобщаем процесс поступления вызовов и принимаем экспоненциально распределенные времена обслуживания.

Диаграмма переходов состояний для полнодоступной системы с потерями с п обслуживающими приборами, процесс поступления вызовов - Кокс-2 (см. рис. 4.10), и экспоненциально распределенным временем обслуживания

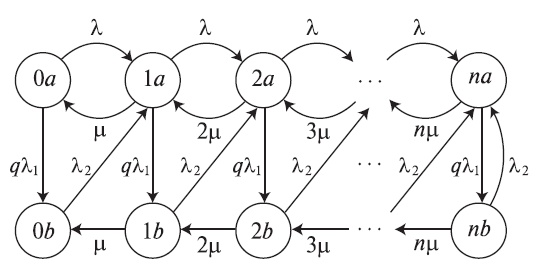
Рис. 9.7. Диаграмма переходов состояний для полнодоступной системы с потерями с п обслуживающими приборами, процесс поступления вызовов - Кокс-2 (см. рис. 4.10), и экспоненциально распределенным временем обслуживания

Краткие итоги

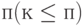В этой лекции рассматривались системы с ограниченной доступностью (неполнодоступные), то есть системы, где абонент или поток нагрузки имеют доступ только к k заданным каналам из общего количества $п(к \le п)$ .
В неполнодоступной системе, если все k каналы заняты, попытка вызова блокируется, даже если среди оставшихся (п-к) каналов есть свободные каналы.
В сетях связи с альтернативной маршрутизацией нагрузка, которая потеряна первичной группой, предлагается группе перегрузки, и она имеет свойства, отличающие её от РСT -нагрузки.
В системе Костена группа разбита на ограниченную первичную группу с п каналами и группой перегрузки с бесконечной емкостью, предлагаемая нагрузка - РСТ1.
Объединенный процесс перегрузки g потоков нагрузки называют эквивалентной нагрузкой перегрузки от единственной полнодоступной группы с тем же самым математическим ожиданием и дисперсией нагрузки перегрузки.
При применении метода ERT мы должны вычислить (m,v) для данных значений (А,n) и наоборот. Это требует применение итерационной процедуры.
Мы можем разбить полную потерянную нагрузку на отдельные пакеты потерянной нагрузки, принимая во внимание, что нагрузка, потерянная для потока i, пропорциональна - средней величине и пиковости потока Z = v/m. (Нагрузка) вероятность блокировки для нагрузки потока i называется вероятностью блокировки пакета.
Фредерике (1980 [29]) предложил метод эквивалентности. Для пико-вости 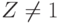$Z \ne 1$ метод Фредерикса и Хэйварда предполагает, что система имеет такую же вероятность блокировки, как система из n/Z каналов с предложенной нагрузкой A/Z, и таким образом пиковость Z= 1. Для последней системы мы можем применить В-формулу Эрланга, при этом следует учитывать, что В-формула Эрланга работает для непрерывного числа каналов.
Башарин и Куренков расширили метод, включив мультислотовую (мультискоростную) нагрузку, где вызов требует d каналов от своего начала и до завершения. Если вызов использует d каналов вместо одного (изменение масштаба), то средняя величина времени становится в d раз больше и дисперсия времени - больше в 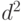раз.
Если нам необходима большая пропускная способность сети, чем предоставляет одиночный канал, то можно параллельно комбинировать больше каналов. В первоначальном источнике мы можем распределить нагрузку (пакеты или ячейки в ATM) циклическим способом по отдельным каналам и в пункте назначения - восстановить первоначальную информацию.
ВРР -модели нагрузки описывают нагрузку двумя параметрами: средней величиной и пиковостью.
Метод Сандера преобразовывает не Пуассоновскую нагрузку (среднее значение, дисперсия) = (т; v) в нагрузку потока с пиковостью Z, прибавляя постоянный поток (нулевая дисперсия) нагрузки со средним значением v-т так, чтобы полная нагрузка имела среднее значение равное дисперсии v.
Если мы рассматриваем полнодоступную группу с п обслуживающими приборами, на которые поступают вызовы, прибывающие согласно IPP с экспоненциально распределенными временами обслуживания, то можем создать диаграмму переходов состояний. Состояние (I, j) обозначает, что есть i обслуживаемых вызовов (i = 0,1,..., n) , а процесс поступления вызовов находится в фазе./ (J = a, если идет процесс поступления вызовов, и j = b, если процесс возвращает вызов). Используя уравнения равновесия узлов, мы находим вероятности состояния равновесия р (i,j) .