|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Процессы поступления заявок
Характеристики точечного процесса
Выше мы обсудили общую структуру точечных процессов. Для заданных приложений необходимо исследовать дальнейшие свойства. Ниже рассматривается только числовое представление, но мы могли сделать то же самое, базируясь на представлении с помощью интервала.
Стационарность (однородность по времени)
Это свойство может быть определено как независимость распределения вероятности, описывающего точечный процесс от позиции на оси времени (момента времени). Следующее определение полезно для практики.
Определение: Для произвольного  и каждого
и каждого  вероятность поступления к заявок на отрезке
вероятность поступления к заявок на отрезке  не зависит от
не зависит от 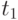 , то есть для всех
, то есть для всех  и
и  мы имеем:
мы имеем:
 |
( 5.15) |
Есть много других определений стационарности - некоторые из них более строгие, другие более слабые.
Стационарность может также быть представлена с помощью интервала, если поставить требование, что все 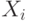 независимы и тождественно распределены ( IID ).
независимы и тождественно распределены ( IID ).
Более слабое определение - это то, что все первые и вторые моменты второго (например, средняя величина и дисперсия) точечного процесса должны быть инвариантным относительно сдвига времени. Эрланг ввёл концепцию статистического равновесия, которое требует, чтобы производные процесса по времени были нулевыми.
Независимость (отсутствие последействия)
Это свойство может быть выражено как требование, что будущая эволюция процесса зависит только от существующего состояния.
Определение: вероятность, что имеет место  событий (
событий (  являются целым числом и
являются целым числом и  ), в промежутке
), в промежутке 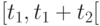 не зависит от событий, которые были перед моментом
не зависит от событий, которые были перед моментом 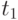
 |
( 5.16) |
Если это справедливо для любого t, то перед нами - марковский процесс: будущая эволюция зависит только от существующего состояния, но независима от того, как оно было получено. Это - отсутствие свойства памяти. Если это свойство справедливо только для некоторых точек (моментов времени), например, времени поступления заявки, то эти точки называются точками равновесия или точками регенерации. Процесс тогда имеет ограниченную память, и мы только должны записать последнюю точку регенерации.
Пример5.2.1: Точки равновесия (точки регенерации)
Примеры точечного процесса с точками равновесия.
- Пуассоновский процесс - как мы увидим в следующей лекции, без памяти, и все точки оси времени - точки равновесия.
- Процесс сканирования, где сканирование делается с регулярным циклом с ограниченной памятью. Последний момент сканирования имеет полную информацию о процессе сканирования, и поэтому все точки сканирования - точки равновесия.
- Если мы предположим, что вышеупомянутый Пуассоновский процесс - сканирующий процесс (например, исследует процессы поступления вызовов в компьютерной системе), то единственные точки равновесия в этом составном процессе - моменты сканирования.
- Рассмотрим систему организации очереди с Пуассоновским потоком вызовов, постоянным временем обслуживания и одним обслуживающим прибором. Число позиций при организации очереди может быть конечно или бесконечно. Пусть к моменту времени, когда начинается обслуживание, существует точечный процесс. Все временные интервалы, если система - простая, будут точками равновесия. В течение периодов, где система занята, моменты времени ввода новых запросов на обслуживание зависят от того, когда начато обслуживание первого вызова в этом периоде занятости.
Простой точечный процесс (ординарность)
Мы уже упомянули (5.7), что исключаем процессы с поступлением в один момент нескольких вызовов.
Определение: точечный процесс называется простым (ординарным), если вероятность, что в данной точке существует больше чем одно событие, является нулевым:
 |
( 5.17) |
В случае представления с помощью интервала распределение интервала поступления не должно иметь нулевой вероятности, то есть распределение в нулевой точке непрерывно (3.1):
 |
( 5.18) |
Пример 5.2.2: Множественные события
Моменты времени дорожных происшествий представляют простой процесс. Число поврежденных автомобилей или погибших людей - непростой точечный процесс с множественными событиями, когда заявки от многих объектов поступают одновременно.
Формула Литла
Это единственный общий результат, который справедлив для всех систем организации очереди. Он был сначала издан Литлом (1961 [75] ). Ниже мы приводим доказательство, применяя теорию стохастического процесса в (Eilon, 1969 [24]).
Мы рассматриваем систему организации очереди, куда поступление заявок от клиентов соответствует стохастическому процессу. Клиенты входят в систему в случайный момент времени и ждут обслуживания. Когда они будут обслужены, они покинут систему. На рис.5.2 процессы и поступления и выхода из системы рассматриваются как стохастические процессы с накопленным числом клиентов (показанным на оси ординат).
Рассмотрим пространство времени  и предположим, что система в начальное время
и предположим, что система в начальное время  находится в статистическом равновесии. Мы используем следующую систему обозначений (рис.5.2):
находится в статистическом равновесии. Мы используем следующую систему обозначений (рис.5.2):
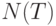 - число поступления заявок в период
- число поступления заявок в период  ;
;
 - полные времена обслуживания всех клиентов в период Т = затененная область между кривыми = величина обслуженной нагрузки;
- полные времена обслуживания всех клиентов в период Т = затененная область между кривыми = величина обслуженной нагрузки;
 - средняя интенсивность вызовов в период
- средняя интенсивность вызовов в период  ;
;
 - среднее время обслуживания одного вызова в период
- среднее время обслуживания одного вызова в период  ;
;
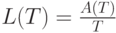 - среднее число вызовов в системе за период
- среднее число вызовов в системе за период  .
.
Выпишем важное соотношение между этими переменными:
 |
( 5.19) |
Если существуют пределы  и
и  , то также существует конечное значение
, то также существует конечное значение  , равное:
, равное:
 |
( 5.20) |
Эта простая формула справедлива для любых систем организации очереди. Доказательство было получено и улучшалось в течение нескольких лет. Мы будем использовать эту формулу в Лекциях 12 -14.

Рис. 5.2. Система организации очереди с поступлением в систему и выходом из системы клиентов. Вертикальное расстояние между двумя кривыми равно фактическому числу обслуживаемых клиентов. Строго говоря, клиенты не выходят из системы в том же порядке, как поступают в нее, так что горизонтальное расстояние между кривыми не описывает фактическое время пребывания клиента в системе.
Пример5.3.1: Формулы Литла
Если мы рассматриваем только места ожидания, то формула показывает, что средняя длина очереди равна интенсивности вызовов, умноженной на среднее время ожидания.
Если мы рассматриваем только обслуживающие приборы, формула показывает, что обслуженная нагрузка равна интенсивности поступления заявок, умноженной на среднее время обслуживания (  )-
)-
Это соответствует определению предложенной нагрузки в секции. 2.1.
Краткие итоги
- Процессы поступления заявок, таких, как телефонные вызовы, прибывающие на станцию, отображаются математически как стохастические точечные процессы.
- В лекции рассматриваются только простые точечные процессы, то есть мы исключаем множественное прибытие, например, одновременное поступления двух вызовов.
- При анализе точечного процесса можно использовать два представления. Представление с помощью интервалов времени соответствует обычному анализу последовательности отсчетов времени; числовое представление не анализирует времени.
- При числовом представлении временной интервал
 сохраняется постоянным, и мы наблюдаем случайную переменную
сохраняется постоянным, и мы наблюдаем случайную переменную  для числа вызовов длительностью
для числа вызовов длительностью  .
. - При представлении с помощью интервалов времени число поступлений вызова сохраняется постоянным, а мы наблюдаем случайную переменную
 для временного интервала до тех пор, пока не поступят
для временного интервала до тех пор, пока не поступят  заявок.
заявок. -
У числового представления есть два свойства, которые представляют теоретический интерес.
- Общее количество поступления заявок в интервале
![[t_1, t_2]](/sites/default/files/tex_cache/3cdd30b6e24f8763136abfe5097d1b5e.png) равно
равно  .
. -
Плотность поступлений вызова за время
 (математическое ожидание времени):
(математическое ожидание времени):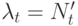
- Общее количество поступления заявок в интервале
-
Чтобы описывать свойства второго порядка для числового представления, мы используем индекс рассеяния для подсчетов - IDC
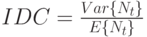
и индекс рассеяния для временных интервалов - IDI
 ,
, -
Стационарность характеризуется следующим свойством: для произвольного
 и каждого
и каждого  вероятность поступления к заявок на отрезке
вероятность поступления к заявок на отрезке ![[t_1; t_1 + t_2 ]](/sites/default/files/tex_cache/69f3ccd3bf0f514963f57af6fa3655ae.png) не зависит от
не зависит от 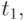 то есть для всего
то есть для всего  и
и  мы имеем:
мы имеем: .
. - Независимость может быть выражена как требование, что будущая эволюция процесса зависит только от существующего состояния.
- Точечный процесс называется простым, если вероятность, что в данной точке существует больше чем одно событие, является нулевым.
-
Для любых систем организации очереди среднее число вызовов в системе за период
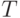 равно
равно .
.
