Производящие функции и рекуррентные соотношения
Применение степенных рядов для доказательства тождеств
С помощью степенных рядов можно доказывать многие тождества. Для этого
берут некоторую функцию и двумя способами разлагают ее в степенной ряд.
Поскольку функция может быть представлена лишь единственным образом в виде
степенного ряда, то коэффициенты при одинаковых степенях  в
обоих рядах должны совпадать. Это и приводит к доказываемому тождеству.
в
обоих рядах должны совпадать. Это и приводит к доказываемому тождеству.
Рассмотрим, например, известное нам разложение

Возведя обе части этого разложения в квадрат, получаем
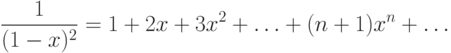 |
( 10.1) |
 на –
на –  , то получим, что
, то получим, что |
( 10.2) |
![\begin{gathered}
\frac{1}
{{(1 - x)^2 }}\frac{1}
{{(1 + x)^2 }} = 1 + [1( - 2) + 2 \cdot 1]x + [1 \cdot 3 + 2( - 2) + 3 \cdot
1]x^2 + \hfill \\
\ldots + [1( - 1)^n (n + 1) + 2( - 1)^{n - 2} n + \ldots + ( - 1)^n (n +
1) \cdot 1]x^n + \ldots \hfill \\
\end{gathered}](/sites/default/files/tex_cache/11a9ed4ec1c40421d36ca285901b98d5.png) |
( 10.3) |
Очевидно, что коэффициенты при нечетных степенях  обращаются
в нуль, каждое слагаемое дважды входит в эти коэффициенты с противоположными знаками.
Коэффициент же
обращаются
в нуль, каждое слагаемое дважды входит в эти коэффициенты с противоположными знаками.
Коэффициент же 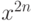 равен
равен
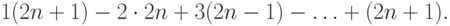
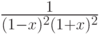 можно разложить в степенной ряд и иным
образом. Мы имеем
можно разложить в степенной ряд и иным
образом. Мы имеем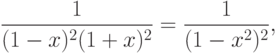
 получается из разложения (10.1), если заменить в нем
получается из разложения (10.1), если заменить в нем  на
на 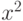 :
: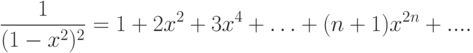 |
( 10.4) |
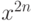 разложении (10.3) должен равняться коэффициенту при
разложении (10.3) должен равняться коэффициенту при 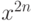 в разложении (10.4). Отсюда вытекает следующее тождество:
в разложении (10.4). Отсюда вытекает следующее тождество: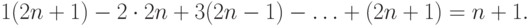
Производящие функции
Пусть дана некоторая последовательность чисел 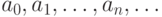 .
Образуем степенной ряд
.
Образуем степенной ряд
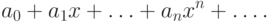
 , то эту функцию называют производящей для
последовательности чисел
, то эту функцию называют производящей для
последовательности чисел 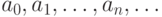 Например, из формулы
Например, из формулы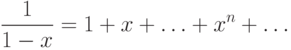
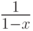 является производящей для
последовательности чисел. А формула (10.1) показывает, что для
последовательности чисел
является производящей для
последовательности чисел. А формула (10.1) показывает, что для
последовательности чисел 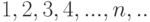 .
производящей является функция
.
производящей является функция 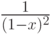 .
.Нас будут интересовать производящие функции для последовательностей 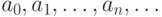 , так или иначе связанных с комбинаторными
задачами. С помощью таких функций удается получить самые разные свойства
этих последовательностей. Кроме того, мы рассмотрим, как связаны
производящие функции с решением рекуррентных соотношений.
, так или иначе связанных с комбинаторными
задачами. С помощью таких функций удается получить самые разные свойства
этих последовательностей. Кроме того, мы рассмотрим, как связаны
производящие функции с решением рекуррентных соотношений.
