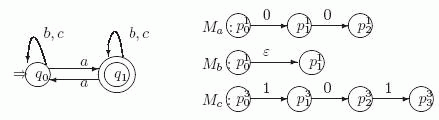| Россия |
Свойства замкнутости класса автоматных языков. Неавтоматные языки
Пример 6.2. Пусть алфавиты 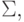
 и гомоморфизм
и гомоморфизм  определены
как выше в примере 6.1. Рассмотрим язык L={ w | число букв а в слове w нечетно }.
определены
как выше в примере 6.1. Рассмотрим язык L={ w | число букв а в слове w нечетно }.
На следующем рисунке показана диаграмма ДКА A, распознающего язык L, и диаграммы
автоматов Ma для 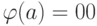 , Mb для
, Mb для  и Mc для
и Mc для 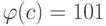 .
.
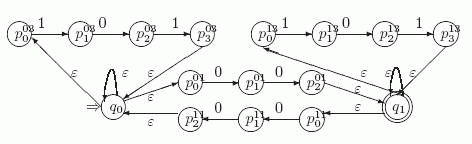
Подставив в A вместо a -переходов автомат Ma, вместо b -переходов автомат Mb и вместо c -переходов автомат Mc, получим представленный на рис. 6.2 недетерминированный
автомат M, распознающий язык  .
На этом рисунке каждая из
.
На этом рисунке каждая из  -петель в состояниях q0 и q1 заменяет
по три
-петель в состояниях q0 и q1 заменяет
по три  -перехода, связанных с Mb.
-перехода, связанных с Mb.
Отметим, что конструкция автомата M в теореме 6.1 удобна для доказательства,
но несколько избыточна.
Без труда можно сократить в ней все  -переходы, склеив
начальные и заключительные состояния автоматов Mi с соответствующими состояниями
автомата A. Например, в автомате на рис. 6.2 можно объединить начальные состояния p00 и p001 с q0, заключительные состояния p201 и p313 с q1 и т.п.
-переходы, склеив
начальные и заключительные состояния автоматов Mi с соответствующими состояниями
автомата A. Например, в автомате на рис. 6.2 можно объединить начальные состояния p00 и p001 с q0, заключительные состояния p201 и p313 с q1 и т.п.
Одним из интересных частных случаев гомоморфизма является проекция.
Определение 6.3.
Пусть 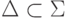 . Проекцией языка L в алфавите
. Проекцией языка L в алфавите  на
подалфавит
на
подалфавит  называется язык
называется язык 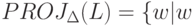 получено из некоторого слова
получено из некоторого слова 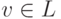 вычеркиванием всех символов,
не принадлежащих алфавиту
вычеркиванием всех символов,
не принадлежащих алфавиту 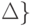 .
.
Определим гомоморфизм 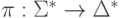 следующим образом:
следующим образом: 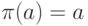 , если
, если 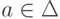 и
и  , если
, если 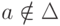 . Тогда для всякого языка L в алфавите
. Тогда для всякого языка L в алфавите  имеет место равенство
имеет место равенство 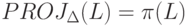 . Отсюда и из предыдущей теоремы 6.1 получаем замкнутость класса автоматных языков
относительно проекции.
. Отсюда и из предыдущей теоремы 6.1 получаем замкнутость класса автоматных языков
относительно проекции.
Предложение 6.2. Для любых алфавитов  и
и  таких, что
таких, что 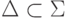 , и любого
автоматного языка L в алфавите
, и любого
автоматного языка L в алфавите  проекция
проекция 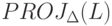 также является автоматным языком.
также является автоматным языком.
Отметим, что для проекции конструкция автомата M для 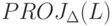 по ДКА A для L
существенно упрощается: достаточно в A все переходы по символам из
по ДКА A для L
существенно упрощается: достаточно в A все переходы по символам из  заменить на
заменить на  -переходы.
-переходы.
Следующая теорема устанавливает замкнутость класса автоматных языков относительного обращения гомоморфизмов.
Теорема 6.2. Пусть 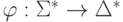 - произвольный гомоморфизм и L - автоматный язык
в алфавите
- произвольный гомоморфизм и L - автоматный язык
в алфавите  Тогда и язык
Тогда и язык 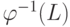 является автоматным.
является автоматным.
Доказательство Пусть 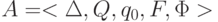 - ДКА, распознающий
язык L.
Пусть
- ДКА, распознающий
язык L.
Пусть 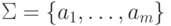 , Q= {q0, q1, ..., qn} и
, Q= {q0, q1, ..., qn} и 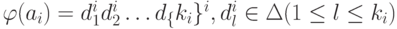 (если
(если 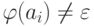 ).
).
Перестроим его в ДКА 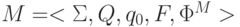 с тем же множеством состояний, начальным и
заключительными состояниями, который
распознает язык
с тем же множеством состояний, начальным и
заключительными состояниями, который
распознает язык 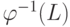 .
.
Идея этого построения состоит в том, чтобы переходить из состояния q
в q' по букве 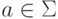 в автомате M, если в автомате A
слово
в автомате M, если в автомате A
слово 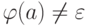 переводит q в q'. Если же для
переводит q в q'. Если же для 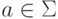 образ пуст, т.е.
образ пуст, т.е. 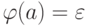 , то в автомате M слово a переводит каждое состояние в себя, так как символы a могут встречаться в каждом слове из
, то в автомате M слово a переводит каждое состояние в себя, так как символы a могут встречаться в каждом слове из 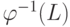 в любом месте и в любом количестве.
в любом месте и в любом количестве.
Таким образом, положим для каждой пары 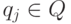 и
и 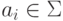
 , если
, если 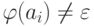 и в автомате A
и в автомате A 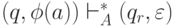 . Если же
. Если же 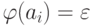 , то полагаем
, то полагаем 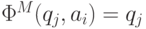 .
.
Так как A - детерминированный автомат, то функция переходов 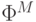 определена однозначно и для всех пар
определена однозначно и для всех пар 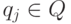 и
и 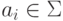 . Следовательно, M детерминированный.
. Следовательно, M детерминированный.
Нетрудно показать, что 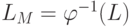 .
.
Действительно, если слово 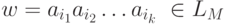 , то в M путь
, то в M путь 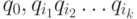 , несущий это слово ведет в
заключительное состояние
, несущий это слово ведет в
заключительное состояние  . Из определения
. Из определения 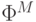 следует, что тогда в A существует
соответствующий путь из q0 в
следует, что тогда в A существует
соответствующий путь из q0 в  , который несет слово
, который несет слово 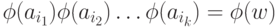 . Следовательно,
. Следовательно,  .
.
Обратно, пусть 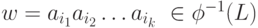 . Тогда слово
. Тогда слово 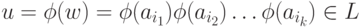 и в автомате A имеется путь,
несущий u, который переводит q0 в некоторое заключительное состояние
и в автомате A имеется путь,
несущий u, который переводит q0 в некоторое заключительное состояние  .
Зафиксируем на этом пути состояния
.
Зафиксируем на этом пути состояния  , в которые он попадает после
прочтения префиксов
, в которые он попадает после
прочтения префиксов 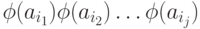 слова u (j = 1, 2, ... , k).
Тогда
слова u (j = 1, 2, ... , k).
Тогда  и для всех j = 1, 2, ... , k имеет место
и для всех j = 1, 2, ... , k имеет место 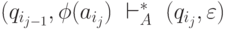 . Отсюда и из определения
. Отсюда и из определения 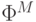 получаем, что в M для всех j = 1, 2, ... , k имеет место переход ха один шаг
получаем, что в M для всех j = 1, 2, ... , k имеет место переход ха один шаг 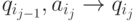 . Следовательно, в M путь q0, q{i1}q{i2}... q{ik}
несет слово w и завершается в заключительном состоянии
. Следовательно, в M путь q0, q{i1}q{i2}... q{ik}
несет слово w и завершается в заключительном состоянии  .
А это означает, что
.
А это означает, что 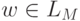 .
.
Пример 6.3. Пусть алфавиты 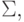
 и гомоморфизм
и гомоморфизм  определены
как выше в примере:
определены
как выше в примере: 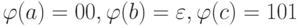 .
Рассмотрим язык L={ w | число букв 0 в слове w нечетно, а число букв 1 - четно}.
.
Рассмотрим язык L={ w | число букв 0 в слове w нечетно, а число букв 1 - четно}.
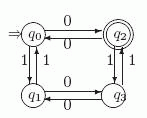
На следующем рисунке показана диаграмма ДКА A, распознающего язык L.
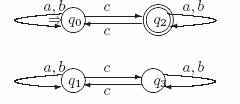
Применив к этому автомату конструкцию из теоремы 6.2, обнаружим, что a и b оставляют все состояния на месте, а c переводит каждое состояние в соседнее состояние "по горизонтали". В результате получаем автомат M, показанный ниже на рис. 6.4.
Легко заметить, что в нем состояния q2 и q3 недостижимы из начального состояния q0 и что этот автомат M распознает язык

Имеется еще много операций, относительно которых замкнут класс автоматных языков. Некоторые из них приведены далее в разделе задач.