| Россия |
Свойства замкнутости класса автоматных языков. Неавтоматные языки
Замкнутость относительно гомоморфизмов и их обращений
Обратимся снова к свойствам замкнутости класса автоматных языков. Как мы уже установили с помощью конструкции произведения автоматов, этот класс замкнут относительно объединения, пересечения и разности (см. следствие 4.1.1). Из теоремы 5.1 непосредственно следует, что класс автоматных языков замкнут относительно операций конкатенации и итерации. Можно легко установить, что он также замкнут относительно дополнения.
Предложение 6.1. Пусть L - автоматный язык в алфавите 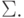 Тогда его дополнение - язык
Тогда его дополнение - язык 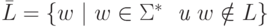 также является автоматным.
также является автоматным.
Действительно, достаточно заметить, что язык 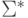 , включающий все слова в алфавите
, включающий все слова в алфавите  является автоматным и что
является автоматным и что 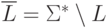 .
.
Определенная ниже операция гомоморфизма формализует идею посимвольного перевода слов одного алфавита в слова другого.
Определение 6.1. Пусть  и Delta - два алфавита. Отображение
и Delta - два алфавита. Отображение 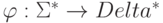 слов первого из них в слова второго называется гомоморфизмом, если
слов первого из них в слова второго называется гомоморфизмом, если

- для любых двух слов w1 и w2 в алфавите
 имеет место равенство
имеет место равенство 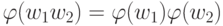 .
.
Из этого определения непосредственно следует, что гомоморфизм однозначно определяется
своими значениями на символах алфавита 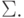 Если w=w1w2 ... wn,
Если w=w1w2 ... wn, 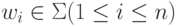 ,
то
,
то 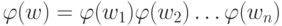 .
.
Пример 6.1.Пусть 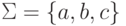 , Delta ={ 0, 1}, а гомоморфизм
, Delta ={ 0, 1}, а гомоморфизм  определен
на символах
определен
на символах  следующим образом:
следующим образом: 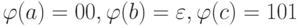 .
.
Тогда 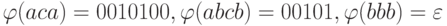 .
.
Определение 6.2.
Пусть 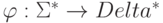 - произвольный гомоморфизм и L - язык
в алфавите
- произвольный гомоморфизм и L - язык
в алфавите 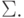 Образом
Образом  языка L при гомоморфизме
языка L при гомоморфизме  называется язык
называется язык 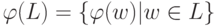 , состоящий из образов всех слов языка L.
, состоящий из образов всех слов языка L.
Пусть L - язык в алфавите  Прообразом этого языка при гомоморфизме
Прообразом этого языка при гомоморфизме  называется язык
называется язык  , состоящий из всех таких слов в алфавите
, состоящий из всех таких слов в алфавите 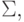 чьи образы при гомоморфизме
чьи образы при гомоморфизме  попадают в L.
попадают в L.
Оказывается, что класс автоматных языков замкнут относительно операций гомоморфизма и обращения гомоморфизма (взятия прообраза)
Теорема 6.1. Пусть 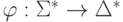 - произвольный гомоморфизм и L - автоматный язык
в алфавите
- произвольный гомоморфизм и L - автоматный язык
в алфавите 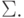 Тогда и язык
Тогда и язык  вляется автоматным.
вляется автоматным.
Доказательство Пусть 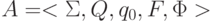 - ДКА, распознающий
язык L. Построим по нему НКА
- ДКА, распознающий
язык L. Построим по нему НКА 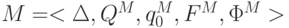 ,
распознающий язык
,
распознающий язык  . Идея этого построения проста: нужно каждый переход из состояния q
в q' по букве
. Идея этого построения проста: нужно каждый переход из состояния q
в q' по букве 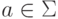 в автомате A превратить в переход из q в q' по слову
в автомате A превратить в переход из q в q' по слову  в автомате M.
в автомате M.
Пусть 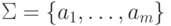 , Q= {q0, q1, ..., qn} и
, Q= {q0, q1, ..., qn} и 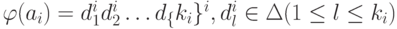 (если
(если 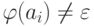 ).
Для каждого ai зафиксируем простой НКА Mi, распознающий язык {d1id2i ... d{ki}i}, имеющий (ki +1) состояние p0i, p1i, ..., p{ki}i и команды p{l-1}dli -> pl (1<= l <= ki).
( Если
).
Для каждого ai зафиксируем простой НКА Mi, распознающий язык {d1id2i ... d{ki}i}, имеющий (ki +1) состояние p0i, p1i, ..., p{ki}i и команды p{l-1}dli -> pl (1<= l <= ki).
( Если 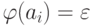 , то у Mi будут два состояния, соединенные
, то у Mi будут два состояния, соединенные  -переходом).
Теперь для каждой команды qj ai -> qr поместим в M между qj и qr автомат Mi (цепочку состояний p0i, p1i, ..., p{ki}i ). Чтобы состояния различных цепочек не
склеивались, придадим им верхний индекс j, т.е. у каждого qj будет своя копия каждого из автоматов Mi.
Для этого
положим
-переходом).
Теперь для каждой команды qj ai -> qr поместим в M между qj и qr автомат Mi (цепочку состояний p0i, p1i, ..., p{ki}i ). Чтобы состояния различных цепочек не
склеивались, придадим им верхний индекс j, т.е. у каждого qj будет своя копия каждого из автоматов Mi.
Для этого
положим 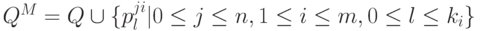 . Таким образом, pl{ji} - это l -ое состояние на пути из qj по "старой" букве ai.
Программа
. Таким образом, pl{ji} - это l -ое состояние на пути из qj по "старой" букве ai.
Программа 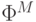 автомата M строится по программе A следующим образом.
Для каждой команды вида qj ai -> qr из
автомата M строится по программе A следующим образом.
Для каждой команды вида qj ai -> qr из  поместим в
поместим в 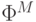 следующие команды:
следующие команды:
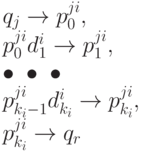
Таким образом, из qj автомат M по пустому переходу попадает в начальное состояние p0ji j -ой копии автомата Mi, затем проходит по слову 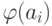 и снова по пустому переходу
попадает в qr.
и снова по пустому переходу
попадает в qr.
Для завершения определения M положим q0M = q0 и FM = F.
Докажем теперь, что наше построение корректно, т.е., что  .
.
-
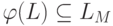 . Заметим вначале, что если
. Заметим вначале, что если  , то
, то  и по определению
и по определению  , следовательно
, следовательно  .
.Пусть
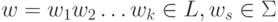 . Тогда в диаграмме A имеется путь из q0 в некоторое
заключительное состояние
. Тогда в диаграмме A имеется путь из q0 в некоторое
заключительное состояние  , который несет слово w. Пусть это путь
, который несет слово w. Пусть это путь 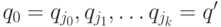 . Тогда для каждого 1 <= x <= k
в
. Тогда для каждого 1 <= x <= k
в  имеется команда
имеется команда 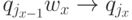 . Но из определения
. Но из определения 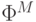 следует,
что тогда в автомате M имеется путь из
следует,
что тогда в автомате M имеется путь из 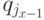 в
в 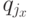 , несущий слово
, несущий слово 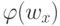 .
Объединив все такие пути, получим путь из из q0 в
.
Объединив все такие пути, получим путь из из q0 в 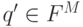 , несущий слово
, несущий слово  .
Следовательно,
.
Следовательно,  .
. -
 . Пусть слово
. Пусть слово  принадлежит LM. Покажем, что тогда
для некоторого
принадлежит LM. Покажем, что тогда
для некоторого 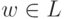
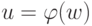 .
Рассмотрим для этого путь в диаграмме M из q0 в
.
Рассмотрим для этого путь в диаграмме M из q0 в 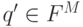 , несущий слово u .
Выделим на этом пути все состояния из Q. Пусть это будут по порядку состояния q0=q{j0}, q{j1}, ... q{jk}= q'. Тогда слово u разбивается на k подслов: u=u1u2 ... uk таких, что ux переводит в M состояние
, несущий слово u .
Выделим на этом пути все состояния из Q. Пусть это будут по порядку состояния q0=q{j0}, q{j1}, ... q{jk}= q'. Тогда слово u разбивается на k подслов: u=u1u2 ... uk таких, что ux переводит в M состояние 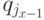 в
в 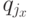 ( 1 <= x <= k ). Покажем, что для каждого такого ux существует символ
( 1 <= x <= k ). Покажем, что для каждого такого ux существует символ 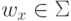 такой, что
такой, что 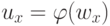 и в
и в  имеется команда
имеется команда 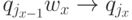 .
Действительно, любой путь из
.
Действительно, любой путь из 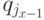 в M начинается
в M начинается  -переходом в некоторое
состояние вида
-переходом в некоторое
состояние вида 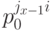 . Пусть это будет состояние на пути, который несет ux в
. Пусть это будет состояние на пути, который несет ux в 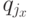 . Далее этот путь обязательно будет проходить
по состояниям вида
. Далее этот путь обязательно будет проходить
по состояниям вида 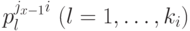 и
завершится
и
завершится  -переходом из
-переходом из 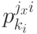 в состояние
в состояние 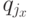 .
Тогда из определения M следует, что
.
Тогда из определения M следует, что  и в
и в  имеется команда
имеется команда 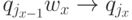 .
Положив wx=ai,
получим, что
.
Положив wx=ai,
получим, что 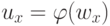 и
и 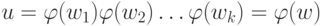 ,
для слова
,
для слова 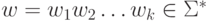 . При этом каждый символ wx этого слова
переводит в автомате A состояние
. При этом каждый символ wx этого слова
переводит в автомате A состояние 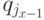 в
в 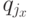 . Поэтому в A
существует путь из q0 в
. Поэтому в A
существует путь из q0 в  , несущий слово w и, следовательно
, несущий слово w и, следовательно