Рекурсия и деревья
Минимакс
Интересным примером стратегии перебора, также естественным образом моделируемой деревом, является минимаксная техника, применяемая в играх, таких как шахматы. Она применима, если справедливы следующие предположения:
- в игре два игрока. Будем называть их Минни и Макс;
- для оценки ситуации, сложившейся в игре, будем использовать оценочную функцию с числовыми значениями, спроектированную так, что отрицательные значения хороши для Минни, а положительные – для Макса.
Минни старается найти позицию, минимизирующую оценочную функцию, а Макс старается ее максимизировать.
Каждый игрок использует минимаксную стратегию для выбора в текущей позиции одного из возможных ходов. Дерево моделирует игры такого вида, последовательные уровни дерева представляют ходы каждого из игроков.
На рисунке все начинается с позиции, где ход должна сделать Минни. Цель стратегии – позволить Минни среди ходов, доступных в данной позиции (три на рисунке), выбрать тот, который гарантирует лучший результат. В данном случае она старается получить минимальное значение оценочной функции на листьях дерева. Метод симметричен, так что Макс использует тот же механизм, стараясь максимизировать выигрыш.
Предположение о симметричности – основа для минимаксной стратегии, которая выполняет обход дерева, чтобы присвоить значение каждому узлу дерева.
| М1 | Значение листа является результатом применения оценочной функции к соответствующей позиции игры. |
| М2 | Значение внутреннего узла, задающего ход Макса, является максимумом из значений детей этого узла. |
| М3 | Значение внутреннего узла, задающего ход Минни, является минимумом из значений детей этого узла. |
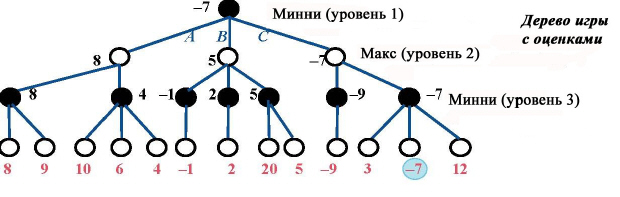
Значением игры в целом является значение, ассоциированное с корнем дерева. Для формирования стратегии следует в случаях М2 и М3 сохранять для каждого внутреннего узла не только значение, но и тот сыновний узел, обеспечивший оптимальную оценку. Вот иллюстрация стратегии, полученной в предположении, что значения в листьях вычислены с помощью некоторой оценочной функции:
Можно видеть, что значение в каждом узле является минимумом (для уровней 1 и 3) или максимумом (на уровне 2) значений сыновей узла. Оптимальный ход для Минни, обеспечивающий значение -7, состоит в выборе хода С.
Перебор с возвратами вполне подходит для минимаксной стратегии, в которой предварительно требуется вычислить значения в листьях и потом присваивать значения в узлах, подымаясь по дереву. Стратегия перебора с возвратами, основанная на принципе? "самый левый в глубину", отвечает такому подходу.
Следующий алгоритм, являясь вариацией ранее приведенной общей схемы перебора, реализует эту идею. Он представлен функцией minimax, возвращающей пару целых: value – гарантированное значение из начальной позиции p, и choice – начальный выбор, приводящий к этому значению. Аргумент l задает уровень, на котором появляется позиция p в ходе игры. Первый ход из этой позиции, возвращаемый как часть результата, является ходом Минни (как на рисунке), если l нечетно, и ходом Макса, если l четно.
minimax ( p: POSITION; l: INTEGER): TUPLE [value, choice: INTEGER]
— Оптимальная стратегия(value + choice) на уровне l, начиная с позиции p.
local
next: TUPLE [value, choice: INTEGER]
do
if p.is_terminal (l ) then
Result := [value: p.value; choice: 0]
else
c := p.choices
from
Result := worst (l )
c.start
until c.after loop
next := minimax (p.moved (c.item), l + 1)
Result := better (next, Result, l )
end
end
end
Для представления результата используется кортеж, задающий значение и выбор.
Дополнительные функции worst и better дают возможность переключаться между Максом и Минни – игрок минимизирует на каждом нечетном ходе и максимизирует на четном.
worst (l: INTEGER): INTEGER
— Худшее возможное значение для игрока на уровне l.
do
if l \\ 2 = 1 then Result := Max else Result := Min end
end
better (a, b: TUPLE [value, choice: INTEGER]; l: INTEGER):
TUPLE [value, choice: INTEGER]
- Лучшее из a и b, в соответствии с их значениями для игрока на уровне l.
do
if l \\ 2 = 1 then
Result := (a.value < b.value)
else
Result := (a.value > b.value)
end
end
Для определения худшего значения для каждого игрока вводятся две константы Max и Min (самое большое и самое малое значения).
Функция minimax предполагает существование следующих методов в классе POSITION:
- is-terminal указывает, что в данной позиции нет ходов, подлежащих исследованию;
- в этом случае value дает значение оценочной функции (запрос value может иметь предусловие is-terminal);
- для нетерминальной позиции пополняется список выборов choices, где каждый выбор представлен целым, задающим допустимый ход;
- если i является таким выбором, moved(i) дает позицию, полученную в результате применения соответствующего хода к текущей позиции.
Простейший способ убедиться, что алгоритм завершается, состоит в ограничении глубины перебора, задав Limit – предельное число уровней. Вот почему is-terminal в том виде, как она задана, включает уровень l как аргумент. Она может быть записана в виде:
is_terminal (l: INTEGER): BOOLEAN
— Следует ли исследовать уровень l или остановиться на текущей позиции?
do
Result := (l = Limit) or choices.is_empty
end
На практике используются более сложные критерии остановки, например, алгоритм может сохранять затраты процессорного времени и останавливаться, когда достигнуто ограничение по времени.
Для выполнения мы вызываем minimax(initial, l), где initial задает начальную позицию игры. Уровень 1 указывает на то, что ход принадлежит Минни.
Альфа-бета
Минимаксная стратегия всегда выполняет полный обход дерева допустимых ходов игры. Можно существенно улучшить эффективность работы, применяя оптимизацию, известную как "альфа-бета-стратегия", которая позволяет пропускать в процессе обхода целые поддеревья, "бесполезные" для достижения цели игры. Это прекрасная идея, заслуживающая внимания не только как "умное" решение, но и как пример усовершенствования рекурсивного алгоритма.
Альфа-бета имеет смысл только в предположениях, сделанных для минимаксной стратегии, когда стратегия одного игрока противоположна стратегии другого (один минимизирует, другой максимизирует), но во всем остальном стратегии игроков идентичны.
Идея пропуска поддерева основана на том, что игрок на уровне l +1 обнаруживает, что нет необходимости продолжать анализировать поддерево, поскольку он может получить на нем лучший результат, чем уже полученный. Но для его противника этот результат будет худшим, чем тот, что уже гарантирован ему на уровне l, и потому противник никогда не выберет это поддерево (напомним, что игроки всегда выбирают оптимальный ход с точки зрения принятой стратегии).
Предыдущий пример позволяет проиллюстрировать идею альфа-бета-стратегии. Рассмотрим ситуацию в процессе работы минимаксного алгоритма, когда исследовано несколько начальных узлов.
Мы находимся в процессе вычисления значения (максимума) для узла Ма1 и, как часть этой цели, вычисления значения (минимум) для узла Мi2. Анализ первого поддерева для Ма1 с корнем в Мi1 позволил определить частичный максимум для Ма1, равный 8 (на рисунке он отмечен знаком вопроса, сигнализирующим, что вычисления еще не завершены). Это означает для Макса, что 8 он себе обеспечил и на меньшее не согласится. При анализе поддерева с корнем Мi2 мы пришли к поддереву Ма2 (к листу в данном конкретном случае, но вывод применим к любому поддереву), где значение равно 6, так что в любом случае Минни не выберет в Мi2 значение, большее 6, а тогда ясно, что дальнейший анализ бесполезен, поскольку не окажет влияния на значение в вышестоящем узле Ма1. Так что, как только найдено значение 6 для Ма2, альфа-бета-стратегия прекратит анализ поддерева с корнем в Мi2.
Эта оптимизация интересна сама по себе, но она дает и хорошую возможность отточить наши навыки рекурсивного программирования. Попытайтесь сами построить соответствующий метод, не заглядывая в решение, которое приводится ниже.
Время программирования!
Адаптируйте минимаксный алгоритм, приведенный ранее, так, чтобы он использовал стратегию "альфа-бета" для отбраковки бесполезных поддеревьев.
Расширение алгоритма достаточно просто. Методу понадобится еще один аргумент, задающий значение (если оно существует), которое для противника гарантированно находится на уровне непосредственно выше. Вот минимаксная процедура с добавленной альфа-бета стратегией:
alpha_beta ( p: POSITION; l: INTEGER; guarantee: INTEGER):
TUPLE [value, choice:
INTEGER]
— Оптимальная стратегия(value + choice) на уровне l, начиная с позиции p.
— Нечетный уровень минимизирует, четный – максимизирует.
local
next: TUPLE [value, choice: INTEGER]
do
if p.is_terminal (l ) then
Result := [value: p.value; choice: 0]
else
c := p.choices
from
Result := worst (l )
c.start
until c.after or better (guarantee, Result, l – 1) loop
next := minimax ( p.moved (c.item), l + 1), Result)
Result := better (next, Result, l )
end
end
end
Каждый игрок теперь останавливает анализ своего выбора, если противник может получить гарантированно лучший результат.
Рекурсивный вызов передает как "guarantee" на следующий уровень лучший Result, полученный на текущем уровне. Как следствие, альфа-бета останавливает обход узлов детей, когда срабатывает новый переключатель выхода better(guarantee, Result, l-1). Такая ситуация никогда не встретится для первого сыновнего узла, поскольку Result инициализирован значением worst.
Минимакс и альфа-бета широко используются в переборных алгоритмах в различных приложениях, где пространство поиска велико. Стратегия "альфа-бета" показывает, как важно в таких ситуациях улучшить стратегию поиска, чтобы избежать анализа возможных, но бесполезных вариантов.