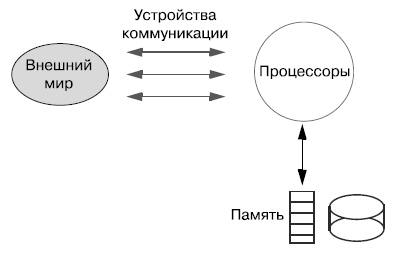
Немного об аппаратуре
Без компьютера ПО работать не может. Для понимания того, как разработать хорошую программу, необходимо понимать, как устроено "железо", на котором эта программа работает. В этой лекции рассмотрим необходимые нам основы устройства аппаратуры, детализируя элементы рисунка, ранее уже показанного:
Начнем с рассмотрения феномена роста характеристик компьютера: объема информации, представленной данными компьютера, скорости доступа к этим данным, скорости выполняемых операций над данными.
Мы сознательно ограничимся лишь теми свойствами, которые необходимы программистам и важны для понимания тем, изучаемых в этом курсе. В какой-то момент вы наверняка прослушаете курс, такой как "Введение в архитектуру компьютеров", который даст вам более глубокие знания по устройству компьютеров.
1.1. Кодирование данных
Данные, хранимые в памяти компьютера, представляют информацию самой разной природы: анкеты работников, фотографии, музыкальные произведения, книги с их разнообразием форматирования, ну и, наконец, численные данные, результаты научных расчетов. Не забудем и о программах, хранимых в памяти. Необходим некоторый общий прием, позволяющий сохранять информацию и должным образом интерпретировать соответствующие данные.
Двоичная система счисления
Двоичная система счисления сделала возможным компьютерную революцию, поскольку открыла простой и общий способ представления информации.
В основе двоичной системы лежат два значения (отсюда "двоичная"). Сами значения не несут особого смысла и их можно называть по-разному: Белые и Черные, Чук и Гек или Изида и Озирис. Имеет значение лишь то, что они различны. Фактически мы будем называть их 0 и 1.
Термин "бит" означает математическую переменную, чьи возможные значения как раз и есть 0 и 1. Он придуман инженерами в конце 1940-го года как сокращение двух слов "binary digit", подчеркивающее, что бит подобен цифрам обычной арифметики (0, 1, … 9), но только с двумя возможными цифрами.
Бит также обозначает техническое устройство с двумя возможными состояниями, следовательно, способное быть представленным математическим битом, стоит только договориться, что есть 0, а что 1. Флажок на кабинете доктора, который может находиться в одном из состояний: "доктор свободен" и "доктор занят" – является битом. Для компьютерной индустрии важную роль играют "электронные" биты, где два состояния соответствуют двум разным напряжениям или намагниченным и размагниченным участкам, как на магнитной ленте или диске.
Причина, по которой двоичная система так хорошо себя зарекомендовала в том, что электроника сделала возможным:
- реализовать физические биты и упаковать их в небольшом объеме – если быть совсем точными, то очень много битов в очень маленькой области. Ниже мы увидим некоторые примеры;
- быстро писать и читать биты. Очень быстро;
- дешево создавать множество таких совокупностей битов. Очень дешево.
Эти свойства обеспечили успех двоичной системе. Некоторые первые компьютеры использовали десятичную систему. Тогда компьютеры рассматривались как машины для вычислений, и казалось естественным для вычислений применять привычную для людей десятичную систему, пришедшую еще с тех давних времен, когда для счета использовались пальцы рук, а пальцев было 10, а не 8, и не 16 (само слово digit – "цифра" – произошло от латинского слова finger – "палец"). Но для компьютеров, построенных на электронике, двоичная система давным-давно вытеснила всех своих соперниц.
Как это касается нас, программистов? В большей степени, чем вы могли подумать. Действительно, программы мы пишем на приятном для нас языке программирования, где попрежнему используем привычную нотацию для записи чисел, например, 3.1415926524. Но, как только приходится рассматривать, как данные хранятся в памяти, сразу же приходится учитывать, что только двоичная система является родной для компьютеров, даже если запись числа выглядит непривычной для людей. Давайте познакомимся с некоторыми свойствами двоичной системы
Основы двоичной системы
Если информация, с которой вам приходится иметь дело, – нечто большее, чем результаты игры в "орёл или решка", то двух значений явно маловато. Базисные комбинации, которыми кодируются конечное множество данных любого размера, являются:
- байт – последовательность из 8 битов;
- слово (word) на новых компьютерах предполагает последовательность из 8 байтов или шестидесяти четырех битов. В прошлые два десятилетия слово обычно означало тридцать два бита, отсюда "64-битная архитектура" и "32-битная архитектура" компьютеров.
Сколько различных значений может задавать последовательность битов? Один бит позволяет задавать два значения: 0 и 1. С двумя битами возможностей становится уже четыре:
В общем случае, последовательность из n битов для любого целого n > 0 задает  значений.
значений.
Базисные представления и адреса
Для базисных единиц:
- байт с его 8-ю битами имеет 256 (
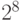 ) различных значений;
) различных значений; - слово из 32 битов имеет
 возможных значений, примерно 4 миллиарда, точное значение приведено в нижеследующей таблице.
возможных значений, примерно 4 миллиарда, точное значение приведено в нижеследующей таблице.
Если, например, мы хотим хранить текст, то можно использовать один байт для хранения каждого символа текста. Может показаться, что 256 различных символов избыточно много для представления текста, но фактически это как раз то, что нужно, поскольку помимо 26 строчных и 26 заглавных букв латиницы необходимы цифры, специальные символы клавиатуры компьютера (такие как ~, !, @ и другие ), акцентированные символы для букв западных языков ( ,
,  ) и так далее. Стандартное кодирование всех этих символов 8-битовым представлением известно как расширенный код ASCII (American Standard Code for Information Interchange). Оригинальный код ASCII использовал только 7 битов (128 значений) и не поддерживал акцентированные буквы.
) и так далее. Стандартное кодирование всех этих символов 8-битовым представлением известно как расширенный код ASCII (American Standard Code for Information Interchange). Оригинальный код ASCII использовал только 7 битов (128 значений) и не поддерживал акцентированные буквы.
Расширенный ASCII код имеет несколько вариантов, наиболее популярный известен как стандарт ISO 8859-1, покрывающий символы наиболее распространенных европейских языков.
Для кириллицы или иероглифов китайского языка расширенного ASCII недостаточно. Стандартом является код Unicode, использующий 4 байта для представления одного символа, что вполне достаточно для всех наиболее важных письменных языков.
Для представления символьных сущностей в Eiffel можно использовать тип CHARACTER_8 для расширенного ASCII или CHARACTER_32 для Unicode. Общим решением является применение типа CHARACTER, который приводится к тому или другому типу в зависимости от конфигурационных установок. С этим мы встретимся в примерах, включающих символьные типы.
Для численной информации общеупотребительной практикой является использование слова для хранения целых значений. Математическое множество целых бесконечно, но память компьютера способна хранить только конечное множество. Если использовать для хранения целых чисел 32-битное слово, оно позволяет задавать примерно два миллиарда отрицательных целых и два миллиарда положительных целых чисел. Для многих приложений этого достаточно. С 64-мя битами границы существенно расширяются. В наших программах тип для целых именуется INTEGER. Целые характеризует и тип CHARACTER. В установках конфигурации целочисленный тип может быть определен как INTEGER_32 или INTEGER_64. Доступны в программах и типы INTEGER_8 и INTEGER_16. Если приходится иметь дело только с неотрицательными целыми, то можно использовать тип NATURAL с его вариантами от NATURAL_8 до NATURAL_64.
Для представления чисел, отличных от целых, – рациональных, таких как 3/2, или иррациональных (вещественных), таких как ?, используются типы REAL_32, REAL_64. Опять-таки можно использовать общий настраиваемый тип REAL. В отличие от целых чисел для представления вещественных значений обычно  значений недостаточно, поэтому чаще для представления вещественных чисел задействуется тип REAL_64.
значений недостаточно, поэтому чаще для представления вещественных чисел задействуется тип REAL_64.
Адресом элемента данных называется его позиция в пронумерованной памяти компьютера. Примеры типов данных: CHARACTER_8, INTEGER_32 и REAL_64 показывают, что элементы данных могут быть различных размеров (1, 4 или 8 байтов). Для обеспечения унификации в адресации памяти за единицу памяти принимается байт, а начальный адрес равен нулю. Так, если память начинается с размещения 1000 значений типа INTEGER_64 на компьютере с 8-байтными словами, то первый свободный элемент памяти имеет адрес 8000.
Степени двойки
Уже по одной той причине, что n битов могут хранить  значений, степени двойки важны для двоичной системы. Ниже перечислены некоторые элементы этой последовательности.
значений, степени двойки важны для двоичной системы. Ниже перечислены некоторые элементы этой последовательности.
Программистам следует помнить первые 10 элементов, порядок и величину других, а также используемые аббревиатуры (кило и другие).
От вишен к байтам
В обычном, десятичном способе счета, аббревиатура "кило" представляет степень 10, точнее,  , которая служит естественной мерой вещей. На рынке мы покупаем один килограмм вишен, равный тысяче –
, которая служит естественной мерой вещей. На рынке мы покупаем один килограмм вишен, равный тысяче –  – грамм, за один миллион –
– грамм, за один миллион –  – долларов вы едва ли купите приличный дом в Южной Калифорнии, один миллиард –
– долларов вы едва ли купите приличный дом в Южной Калифорнии, один миллиард –  – долларов может продлить на несколько часов существование банка, падающего во время кризиса.
– долларов может продлить на несколько часов существование банка, падающего во время кризиса.
Эти единицы применимы и к другим измерениям, связанным с компьютерами, не только по отношению к памяти.
- Обмен данными по линии может проходить со скоростью в 1 Mbps (Megabit per second) – один Мегабит за секунду.
- Центральный процессор может работать со скоростью в 1 GHz (Gigaherz – Гигагерц), выполняя один миллиард базисных операций процессора за секунду. "Герц" – термин, заимствованный у физики, единица измерения частоты.
Компьютерные инженеры предпочитают использовать степени двойки для выражения размеров памяти. Здесь и начинается путаница. Точнее, она началась, когда некто (имя его не сохранилось в истории) заметил, что два в десятой степени равно 1024, что примерно равно  – тысяче, и как следствие принял блестящее решение использовать десятичные аббревиатуры – кило для почти-тысячи (
– тысяче, и как следствие принял блестящее решение использовать десятичные аббревиатуры – кило для почти-тысячи ( ), мега для почти-миллиона (
), мега для почти-миллиона (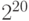 ), гига для почти-миллиарда (
), гига для почти-миллиарда ( ). С ростом степеней аппроксимация становится все хуже, как видно из таблицы.
). С ростом степеней аппроксимация становится все хуже, как видно из таблицы.
Двоичная интерпретация тысячи наряду с традиционной иногда приводит к неразберихе, особенно если обе интерпретации применяются совместно. На вышедших уже из употребления флоппи-дисках их емкость указывалась как 1.44 МВ, но означало это 1440 (десятичная интерпретация) раз по 1024 (двоичная интерпретация) байтов.
Чтобы покончить с беспорядком, соответствующая организация, занимающаяся стандартами, предписала применять десятичные аббревиатуры – кило и другие – для степеней 10, а для степеней двойки применять другие аббревиатуры – киби, меби, гиби, приведенные в последнем столбце таблицы. Эти имена не получили широкого распространения.
Во избежание недоразумений помните, что двоичная интерпретация применяется только для измерения памяти, в остальных случаях применяется десятичная. Так что 1-GHz компьютер с памятью в 1 GB выполняет один миллиард операций в секунду, но памяти имеет больше чем один миллиард, – на 73 миллиона байтов больше. На практике разница не столь уж велика: что для нас десяток-другой миллионов?