Немного об аппаратуре
Действия над числами
Представление целых чисел в компьютере хорошо тем, что оно точно. Действия над целыми выполняются точно так же, как это принято в математике. Плохо лишь то, что целые в компьютере составляют конечное подмножество, в отличие от математики. Для 64-битного компьютера множество целых определяется диапазоном: 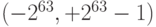 .
.
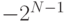 ), а верхняя (
), а верхняя (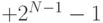 ), так что максимальное по модулю отрицательное число на единицу больше максимального положительного числа. Дополнительный код строится так, чтобы поразрядное сложение n и –n в двоичной системе давало ноль. Для положительных целых старший разряд в представлении числа N битами является знаковым и равен нулю, так что на само число остается N-1 бит, что и дает верхнюю границу. Отрицательные числа строятся добавлением единицы к обращению положительного числа (под обращением понимается взаимная замена 0 и 1). При N = 4 число 5 будет храниться как 0101, а число -5 – как 1011.
), так что максимальное по модулю отрицательное число на единицу больше максимального положительного числа. Дополнительный код строится так, чтобы поразрядное сложение n и –n в двоичной системе давало ноль. Для положительных целых старший разряд в представлении числа N битами является знаковым и равен нулю, так что на само число остается N-1 бит, что и дает верхнюю границу. Отрицательные числа строятся добавлением единицы к обращению положительного числа (под обращением понимается взаимная замена 0 и 1). При N = 4 число 5 будет храниться как 0101, а число -5 – как 1011.Для допустимых значений целых точным является не только их представление – результаты операций над целыми дают те же значения, что и их математические двойники, за исключением тех случаев, когда значения результатов выходят за пределы, допустимые для целых. Написав a + b для целых a и b, получим корректный результат, если он не больше максимального или не меньше минимального значения. Выход результата за допустимые пределы известен как "арифметическое переполнение".
Представление вещественных чисел – REAL-тип, как он называется в Eiffel (float – в других языках), аналогично представлению целых в том отношении, что задает конечное множество возможных значений. Как следствие, представление вещественных чисел частично и не всегда точно. В математике между любыми двумя вещественными числами находится бесконечно много других вещественных чисел. Это же справедливо и для рациональных чисел – менее мощного подмножества вещественных чисел, так что даже все рациональные числа не могут быть точно представлены в памяти компьютера. В этом отражается типичная разница между информацией и хранимыми данными.
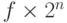 , со знаком s.
, со знаком s.Эти свойства отражаются в программе тремя способами.
- Когда вещественное число x задается в программе явно программным текстом, или читается из файла, или поступает от датчиков или других устройств, то хранимое его значение является представимым значением вещественного типа, близкого к значению x, но не гарантированно с ним совпадающего.
- Арифметические операции – сложение, умножение, вычитание, деление, возведение в степень – могут быть невыполнимыми, хотя математически их результат строго определен. Переполнение (Overflow), упоминаемое выше для целых, здесь также возможно. Если x и y – два представимых вещественных числа (предположим для определенности, что они положительны), то
 или
или  могут быть слишком большими для представления. Еще один пример, характерный уже только для вещественных чисел: деление
могут быть слишком большими для представления. Еще один пример, характерный уже только для вещественных чисел: деление 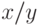 , где y не равно нулю, но мало, так что результат в математике определен, но слишком велик для представления в системе компьютера. Для вещественных чисел возможно возникновение ситуации, называемой "Переполнение снизу" (underflow), которая может возникать, например, при делении x / y, когда y слишком велико и результат слишком мал по абсолютной величине,
чтобы он мог быть представлен значением, отличным от нуля (в этом случае говорят, что результат является "машинным" нулем).
, где y не равно нулю, но мало, так что результат в математике определен, но слишком велик для представления в системе компьютера. Для вещественных чисел возможно возникновение ситуации, называемой "Переполнение снизу" (underflow), которая может возникать, например, при делении x / y, когда y слишком велико и результат слишком мал по абсолютной величине,
чтобы он мог быть представлен значением, отличным от нуля (в этом случае говорят, что результат является "машинным" нулем). - Даже в отсутствие переполнений сверху и снизу арифметические операции могут стать причиной возникновения ошибок. Если x' и y' являются представимыми значениями x и y, то программистская нотация
 не обозначает математическую нотацию суммы x и y, она даже не может представлять точное значение суммы
не обозначает математическую нотацию суммы x и y, она даже не может представлять точное значение суммы  , поскольку не гарантируется представимость результата. Любой алгоритм, имеющий дело с вещественными числами, должен принимать в расчет эти ограничения.
, поскольку не гарантируется представимость результата. Любой алгоритм, имеющий дело с вещественными числами, должен принимать в расчет эти ограничения.
Об этом непрестанно приходится заботиться в "численных расчетах", используемых не только в научных или инженерных проектах, но и, например, в финансовом моделировании, где также применяются вещественные числа и численные алгоритмы. Ошибка в каждой операции незначительна и может быть совсем не страшной для результата. Плохо, когда эта ошибка накапливается в процессе выполнения миллионов и миллиардов операций, что в конечном итоге может привести к серьезным ошибочным следствиям и искажению результатов.
Численное программирование требует особых подходов, позволяющих избегать подобных неприятностей. Рассмотрим простой пример – в одной из последующих лекций мы встретимся с методом интегрирования, приближенно вычисляющим значение определенного интеграла:

Алгоритм может быть реализован циклом. Покажем сейчас фрагмент алгоритма, а его полная версия появится позже. Во фрагменте используется локальная переменная x типа REAL:
from x := low until x >= high loop
Result := Result + f.item ([x]) — f.item ([x])дает значение f(x).
x:=x+step
end
Листинг
1.1.
В принципе, все работает, но обратите внимание на то, как x обновляется на каждой итерации. На каждом шаге добавляется переменная step, что приводит к появлению незначительной ошибки, но от итерации к итерации эта ошибка накапливается и может стать причиной существенного отклонения в процессе общего вычисления.
Некоторые программисты используют форму вычислений, подобную [1.1], полагая, что исключение умножения ускорит вычисление. Это, может быть, и справедливо, но эффект от накопления погрешности опасен. Разумная реализация вышеприведенной формулы использует умножение:
from x := low until x >= high loop
Result := Result + f.item ([x]) — f.item ([x]) дает значение f(x).
i := i + 1 ; x := low + (i * step) - [2]
end
Листинг
1.2.
Прямое вычисление x на каждом шаге позволяет избежать накопления погрешности. В худшем случае мы получаем ошибку, возникающую в результате выполнения одного сложения и одного умножения. Вот общий принцип:
Почувствуй методологию
При разработке ПО, включающего действия с вещественными числами, учитывайте приближенный характер вычислений. При проектировании алгоритма избегайте накопления вычислительных погрешностей.
В краткой форме этот совет звучит так: изучайте вычислительную математику – часть прикладной математики, имеющей дело с численными вычислениями в противоположность символьным вычислениям. В этом курсе подробно рассматриваются свойства и ограничения представления чисел и операций, выполняемых на компьютере.
В ненадежной стране численного программирования существует надежное место: стандартизация. Ранее каждая компьютерная система имела собственную систему представления чисел и операций, из-за чего нельзя было гарантировать, что математически корректный алгоритм будет корректно работать на компьютере. Ситуация исправилась с введением стандарта IEEE на архитектуру арифметики с плавающей точкой. Этот стандарт определяет единые рамки для системы чисел компьютеров как с 32-битной, так и с 64-битной архитектурой. Большинство современных компьютеров соответствуют этому стандарту. Так что, если нужно проверить, что алгоритм не является причиной появления неприемлемых вычислительных погрешностей, то такую работу нужно проделать только однажды, полагаясь на стандарт.
1.2. О памяти
В памяти мы храним данные и извлекаем их по мере необходимости. На нижнем уровне представления в памяти хранятся символы, но для наших программ память представляется хранилищем, в которое можно помещать и получать объекты. Давайте разберемся, что память может делать в наших интересах.
Живучесть
На первом рисунке этой лекции для изображения памяти используются два различных символа, отражающие два вида памяти с различными требованиями.
- Преходящая, кратковременная или оперативная, память хранит данные, создаваемые и обрабатываемые во время выполнения программы, но не гарантирует, что они сохранятся с окончанием этого сеанса выполнения. Технологически такая память при выключении электроэнергии теряет хранимые в ней данные.
- Постоянная память, обеспечивающая живучесть данных, сохраняет данные и при выключении энергии, при условии, конечно, что данные не удаляются явным образом.
Зачем нужна кратковременная память? Не было бы проще, чтобы все данные хранились вечно по умолчанию? Есть две причины, по которым это не делается, – технологическая и экономическая. Память, доступная процессорам во время выполнения, должна быть очень быстрой и, как следствие, является дорогой. Постоянная память значительно дешевле, так что ее можно использовать для хранения больших объемов информации – текстов, рисунков, музыки, расписания полетов, персональных данных и т. д., доступ к которым более медленный.
Слова: приемлемая или медленная скорость, большие или малые объемы, дорогая и дешевая – нельзя рассматривать вне контекста. Вот некоторые оценки (на момент написания оригинала курса).
- Компьютер, подходящий для разработки ПО, возможно, ноутбук, может иметь оперативную память в несколько гигабайт стоимостью в несколько сотен долларов за память. Время доступа к символу составляет примерно 50 наносекунд, что позволяет за секунду получить 20 миллионов символов (одна наносекунда – ns – равна
 секунды).
секунды). - Компьютер может иметь диск (постоянную память) емкостью в сто раз больше оперативной памяти – в несколько сот гигабайт, стоящий вдвое дешевле, со скоростью доступа порядка 5 миллисекунд.
Как видите, время доступа к оперативной и постоянной памяти существенно различается, что непосредственно значимо для программиста. Программы, которые обрабатывают большие объемы данных, не могут игнорировать проблемы распределения и обмена данными между постоянной и оперативной памятью. Следует тщательно управлять временем передачи данных, чтобы сохранить приемлемое время выполнения приложения.
Оперативная память
Как отмечалось, операции процессора получают доступ к оперативной памяти. Этот ключевой компонент вычислений имеет несколько имен:
- главная память;
- первичная память;
- RAM-память (Random Access Memory – память со случайным доступом).
Последний термин имеет исторические корни. Вначале постоянная память, в отличие от первичной, была реализована технологически на магнитных лентах, а еще ранее – на перфорированных бумажных ленточках, где дырка в нужном месте задавала бит, равный 1, а отсутствие дырки означало, что значение бита равно 0. Доступ к данным на такой ленте был последовательным, так что время доступа к тому или иному биту зависело от его адреса; нужно было перемотать ленту, прежде чем прочесть значение бита. Оперативная память того времени была реализована как память прямого доступа. Время доступа к любому элементу не зависело от его адреса, поэтому такая память и получила название RAM-памяти. Теперь, конечно, и память на дисках является памятью прямого доступа, но название RAM все еще сохранилось для оперативной памяти;
- ферритовая (Core) память. Термин опять восходит к старым технологиям, когда элементами памяти служили ферритовые намагниченные сердечники – ферритовые ядра, так что до сих пор можно услышать, что множество данных хранится "в ядре".
На ниже представленной фотографии показана главная память – чип (микросхема), на два GB, изготовленная по технологии "DDR2_800", обеспечивающая время цикла в 5 наносекунд с пиковой производительностью передачи данных в 6,4 гигабайта в секунду.
Разнообразие постоянной памяти
Существует два вида постоянной памяти.
- Некоторые элементы рассматриваются как часть компьютера и присоединены к нему постоянно. Они называются вторичной памятью, чтобы подчеркнуть тот факт, что они фактически являются продолжением первичной памяти. Их положительной стороной (помимо обеспечения живучести данных) является относительно низкая стоимость доступа, позволяющая сохранять сотни гигабайт. Обратная сторона медали – доступ значительно медленнее, чем к первичной памяти, и процессорам эта память непосредственно недоступна. Чтобы обработать данные, хранимые в этой памяти, они предварительно должны быть прочитаны в оперативную память.
- Другие элементы памяти присоединяются к компьютеру эпизодически на момент копирования данных, а затем могут быть удалены. Позже они могут быть присоединены к этому же или к другому компьютеру. В частности, они служат для хранения "резервных копий" данных. Они также называются съемной памятью или сменными хранилищами (storage) – синонимами памяти.
Наиболее общей формой вторичной памяти является диск. Более корректный термин – дисковод или дисковое устройство, включающее несколько дисков на одном стержне, вращающихся в процессе работы со скоростью от 4000 до 12000 оборотов за секунду. Данные считываются или записываются специальными головками, которые могут перемещаться над рабочей поверхностью вращающихся дисков. Значение считываемых или записываемых битов зависит от намагничивания небольших областей диска. Если выключить энергию, то диск вращаться не будет и операции записи и чтения становятся невозможными, но намагничивание остается, что и гарантирует сохранность данных на диске.
Устройство, показанное на рисунке, имеет два диска, хотя вы видите только один. Оно может хранить 8 гигабайт (если это вас не впечатляет, то скажу, что это модель 1999 года, но я пока не намерен разобрать свой новейший дисковод, чтобы показать вам его фотографию. В магазине на момент написания этого текста нетрудно приобрести диск на несколько сот гигабайт стоимостью в 50$, терабайтные диски также вполне доступны). Дисковод на рисунке обеспечивал скорость вращения 5400 оборотов в секунду со временем доступа в 9 миллисекунд и максимальной скоростью передачи данных в 33 мегабайта за секунду. Время доступа и передачи указаны приблизительно, поскольку важной характеристикой является латентное время – время задержки, связанное с перемещением головки диска к нужной дорожке, после чего получить требуемые данные на дорожке можно много быстрее. Когда разрабатываются программы, в которых предусмотрена интенсивная работа с диском, нужно учитывать это свойство для оптимизации производительности.
Пока еще диски остаются доминирующим видом постоянной памяти, но уже появился серьезный конкурент в виде SSD-устройств, использующих флеш-память (SSD – Solid-state drive – полупроводниковый или твердотельный диск). В отличие от дисков SSD являются чисто электронными устройствами (а не электромеханическими, где перемещение головок обеспечивается механическим устройством) и не включают никаких подвижных частей. Они не подвержены "разрушениям диска", традиционным для "дисковой" технологии, когда в результате все данные на диске будут потеряны без всякого предупреждения.
Недостатком флеш-памяти является то, что она поддерживает только ограниченное число перезаписываний, хотя уже есть способы, позволяющие справиться с этим ограничением. Уже к концу 2008 года SSD стали привлекательной альтернативой дискам даже для ноутбуков, благодаря быстро возрастающей емкости и уменьшению цены.
Портативный компьютер – лэптоп, MIT Media Lab's XO laptop, – введенный в 2007 году как часть проекта "Каждому ребенку – свой лэптоп" (OLPC project – One Laptop Per Child), был одним из первых компьютеров, спроектированных для широкого распространения в мире, и использовал флеш-память, а не диски.
Следуя традициям бумажных лент, упомянутых ранее, некоторые устройства памяти являются съемными. Среди наиболее популярных являются USB-устройства, называемые так потому, что они связаны со стандартизованной последовательной шиной для передачи данных (Universal Serial Bus). Они используют технологию флеш-памяти емкостью от 2-х до 16 гигабайт, а теперь и больше. Съемными теперь являются и USB-диски, устроенные так же, как и встроенные диски, но присоединяемые к USB-порту, что и обеспечивает возможность их смены. Емкость таких дисков начинается от 100 GB.
Регистры и иерархия памяти
Операциям, таким как сложение, требуются операнды, которые чаще всего должны находиться в специальных элементах памяти, называемых регистрами. Большинство архитектур имеют не более нескольких десятков регистров. Для выполнения операции над операндами, хранимыми в обычной оперативной памяти, например, для a и b в присваивании
a := a + b
необходимо выполнить следующие действия: прочесть значения a и b из оперативной памяти и записать их в соответствующие регистры, выполнить операцию над ними, в данном случае сложение, из регистра результата записать в оперативную память в область, отведенную для a.
Как результат, базисная иерархия памяти имеет три уровня:
- регистры, число которых мало, но скорость сравнима со скоростью центрального процессора;
- первичная память, ядро, емкостью в несколько гигабайт, но более медленная;
- диск или его эквивалент в несколько сот гигабайт емкостью, но еще более медленный.
Типичный порядок времени записи к моменту написания этого текста составлял: 0,5 наносекунды, 50 наносекунд и 5 миллисекунд. Цифры могут со временем изменяться довольно быстро, но порядок отношения обычно остается. Рассмотрим в частности отношение между двумя последними видами памяти, примерно равное 100000. Спроецируем эти отношения на человеческий уровень выполнения работ. Вообразите рабочего, который:
- способен обработать деталь, если она уже находится в нужном месте, за 0.01 секунды (аналог операций процессора, когда операнды помещены в регистры);
- получать заготовку из рядом расположенного хранилища, тратя на это одну секунду (аналог главной памяти, большой, но все же ограниченной);
- получать неограниченное количество заготовок от поставщика, удаленного за сотни километров, так что на доставку уходят целые сутки.
Для компьютера все цифры нужно делить на 20 000 000, но соотношение остается тем же самым. Политика управления памятью – что хранить в оперативной памяти, что на диске – существенно влияет на производительность.
Виртуальная память
На практике различие между главной памятью и дисковой затушевывается ввиду доступности виртуальной памяти, предоставляемой операционной системой. В результате можно считать, что основной памяти значительно больше той реальной памяти, за которую мы заплатили.
Виртуальная память предоставляет программисту адресное пространство, значительно превосходящее физическое адресное пространство. Система управления памятью, стоящая за сценой, обеспечивает подкачку нужных данных с диска, когда они требуются, но не находятся в первичной памяти. Технически вся память разделяется на единицы, называемые страницами, каждая обычно размером в несколько килобайт. Фактический доступ к данным требует, чтобы они были в ядре, если это не так, то возникает ошибка доступа к странице, система виртуальной памяти в этом случае загружает соответствующую страницу из диска – эта операция называется "загрузка страницы" (page in). При загрузке страницы может возникнуть ситуация, когда физическая память использована и для страницы уже нет места. В этом случае предварительно произойдет "выгрузка страницы" на диск (page out). Есть разные сценарии, позволяющие выгружать страницы, которые с большой долей вероятности не понадобятся в ближайшее время.
Причина, по которой эта политика может быть эффективной, состоит в том, что в периоды интенсивной работы, обрабатывая циклы, программа использует небольшое подмножество – рабочее подмножество – из всего адресного пространства. Только в экстремальных ситуациях такая стратегия приводит к трешингу – режиму интенсивной подкачки, когда операции загрузки и выгрузки страниц беспрерывно сменяют друг друга.
Виртуальная память также облегчает режим разделения времени, когда компьютер выполняет одновременно несколько программ. Каждая программа в этом случае полагает, что у нее собственное адресное пространство, которое в реальности отображается на множество страниц, не пересекающихся в ядре, и на диске с адресными пространствами других программ.
Все это, конечно, затрудняет оценку производительности наших программ, так как реально не известно, в какой момент может возникнуть ситуация ошибки доступа к странице. Это похоже на ситуацию с нашим мифическим рабочим, который, обратившись в хранилище за заготовкой, вдруг обнаруживает, что оно пусто и требуются сутки, чтобы доставить деталь. Однако в большинстве практических случаев эти соображения можно игнорировать и полагать, что у вас реально есть, скажем, 20 GB, когда физически их только 4.