Немного об аппаратуре
1.3. Команды компьютера
В обычных ситуациях командами, с которыми имеет дело программист, являются операторы языка программирования. Полезно, однако, понимать, в какие фактические команды компьютера транслируются операторы языка программирования – те команды, которые только и может выполнять компьютер.
Типичная команда компьютера хранится в слове памяти, иногда в нескольких словах. Она содержит код команды, определяющий ее тип – операцию, выполняемую командой, а также ноль или более требуемых аргументов, которые могут быть адресами или значениями. Для примера рассмотрим команду компьютера с архитектурой 32-битного Power PC. Команда занимает слово (32 бита) с нумерацией битов, начинающейся с нуля:
Код команды является комбинацией первичного кода 31 (двоичное 11111), заданного битами от 0 до 5, и вторичного кода 266 (двоичное 100001010) в битах от 22 до 31. Результат помещается в регистр 5 (двоичный код 101), а операнды читаются из регистров 3 и 4.
Компьютеры обладают командами трех разных типов.
- Вычисления: арифметические операции, такие как сложение (в приведенном примере), вычитание, умножение, деление с вариантами для целых и вещественных чисел, операции сравнения, побитовые операции, которые выполняют логические операции над соответствующими парами битов двух слов. Обычно такие операции выполняются над операндами, расположенными в регистрах.
- Загрузки и хранения: передают данные из оперативной памяти в регистры и обратно, а также обеспечивают передачу данных с другими устройствами аппаратуры.
- Управления: переключая выполнение к другой точке программного кода в зависимости от выполнения некоторого условия или осуществляя безусловный переход.
Каждая команда имеет свой код, такой, как 31 в примере. Более удобно ссылаться на код команды, используя мнемонику. Для Power PC мнемоника команды сложения с кодом 31 – add. Представление программы в машинных командах не является удобной формой для общения с человеком. Язык ассемблера обеспечивает приемлемую, доступную для восприятия человеком форму представления таких программ. На языке ассемблера Power PC рассмотренная нами команда может быть записана так:
add r5, r3, r4
Язык ассемблера заимствовал у языка программирования возможность применения символических имен: имя регистра, такое как r5, имя команды, такое как add, – так же как использование идентификаторов для адресов и констант. Ответственность за трансляцию ассемблерного кода в машинный код ложится на программную систему, называемую ассемблером, которая представляет простейший вид компилятора. Трансляция облегчается тем, что для языка ассемблера выполняется соответствие "один в один" – одна команда ассемблера, как правило, транслируется в одну машинную команду компьютера. Операторы языка программирования задают куда более высокий уровень абстракции. Еще одна особенность ассемблера состоит в том, что для каждой архитектуры компьютера есть свой язык ассемблера, связанный с этой архитектурой. Современные языки программирования являются переносимыми (независимыми от платформы). Не будучи в полном смысле этого термина языком программирования, язык ассемблера позволяет преодолеть наиболее утомительные моменты, связанные с написанием и чтением программ в машинном коде.
Что должно остаться в памяти после всех этих обсуждений? Тот провал между командами, которые может выполнять компьютер, и теми задачами, которые мы хотим решать с помощью компьютера. Это доказывает важность языков программирования и объясняет сложность разработки ПО.
1.4. Закон Мура и эволюция компьютеров
При рассмотрении влияния производительности аппаратуры на программирование нельзя не учитывать ось времени. Чрезвычайные успехи информационных технологий идут рука об руку с прогрессом в разработке аппаратуры. В 1965 году появилась статья Гордона Е. Мура (Gordon Moore), сооснователя корпорации Intel, в которой он в чрезвычайно яркой форме описал этот феномен. Наибольшую известность получил так называемый "закон Мура", формулируемый следующим образом: "Число компонентов, размещаемых на интегральной схеме при сохранении постоянной стоимости, удваивается каждые 18 месяцев" (заметим, что сам Мур говорил о двух годах, но потом эта константа была уменьшена по результатам наблюдений до полутора лет). Есть несколько вариантов этого закона, но все они говорят об экспоненциальном росте. Эти утверждения не являются в полном смысле этого слова "законами", такими, как законы, открытые Максвеллом, Ньютоном или Эйнштейном. Это наблюдения о прогрессе индустрии в течение нескольких десятилетий – наблюдения, которые оказались пророческими и до сих пор продолжают быть применимыми. Удивительно, что нет никакой другой области человеческой деятельности, хоть сколько-либо напоминающей столь удивительную скорость роста. Автомобили сегодня не в тысячу раз быстрее, чем 20 лет назад.
В то время как закон, сформулированный Муром, говорил о плотности размещения элементов на интегральной схеме, а тем самым, и о скорости обработки, варианты этого закона говорили о том же феномене, справедливом и для многих других аспектов, – размере памяти, скорости доступа, стоимости различных устройств. Я помню, что был поражен (немногим более десятилетия назад), когда стоимость мегабайта дисковой памяти опустилась ниже одного доллара. Сегодня не многие готовы платить доллар за гигабайт.
Основной закон Мура не может быть беспредельно устойчивым, поскольку размещение все большего числа элементов в ограниченном пространстве приводит к росту излучаемого тепла, а кроме того, есть чисто физические пределы скорости распространения сигнала. В результате, как говорят некоторые компьютерные архитекторы: "число людей, объявляющих, что закон Мура перестал действовать, удваивается каждые полтора года". Фактически, закон продолжает действовать, но на новом уровне. Решение дают параллельные вычисления. Не нужно создавать процессор, работающий еще быстрее. Можно создать несколько процессоров, работающих параллельно. Многоядерная архитектура компьютеров становится общепризнанной. Проблема в том, что пока нет удовлетворительного решения, позволяющего программистам использовать все преимущества параллельной архитектуры. Но ни слова больше на эту тему. Эта проблема требует отдельного курса.
1.5. Дальнейшее чтение
Стандарт IEEE для арифметики с плавающей точкой, доступный по адресу: ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=4610935
John Markoff: Faster Chips Are Leaving Programmers in Their Dust, in New York Times, December 2007, доступна по адресу: tinyurl.com/5cstbq.
John L. Hennessy and David Patterson; Computer Architecture, Fourth Edition: A Quantitative Approach, Morgan Kauffmann, 2006.
1.6. Ключевые концепции, изученные в этой лекции
- Внутреннее представление данных в компьютере использует двоичную систему.
- Базисной единицей данных является бит с двумя возможными значениями: 0 и 1. Биты группируются в байты, содержащие 8 битов, и слова, обычно из 8-ми или 4-х байтов (64-битная или 32-битная архитектура). Адреса измеряются в байтах. Целые и вещественные числа обычно хранятся в словах. Существуют также более компактные представления из одного или двух байтов. Символы представлены одним байтом (расширенный ASCII) или двумя байтами (Unicode).
- Измерение величин, отличных от единиц памяти, например скорости, всегда использует десятичные единицы, такие как кило (тысяча), мега (миллион), гига (миллиард), тера (
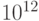 ), пета (
), пета ( ). Для описания размеров памяти и адресов общей практикой, несмотря на официальные стандарты, принято использовать те же префиксы (кило и другие) для степеней двойки, начиная с
). Для описания размеров памяти и адресов общей практикой, несмотря на официальные стандарты, принято использовать те же префиксы (кило и другие) для степеней двойки, начиная с  и примерно равное
и примерно равное  .
. - Представление целых в компьютере является точным, но только в конечном интервале.
- Представление вещественных чисел является приближенным. Арифметические операции являются обычно источником появления погрешностей. Реализация численных алгоритмов должна избегать накопления таких ошибок.
- Иерархия памяти включает регистры, оперативную память и устройства постоянной памяти, такие как диски и флеш-память. Операции процессора применимы к операндам, хранимым в регистрах. Доступ к регистрам – самый быстрый (менее наносекунды), но число регистров невелико. Оперативная память на сегодняшний день имеет порядок нескольких гигабайт со временем доступа примерно в 100 раз более медленным, чем доступ к регистрам. Эта память при отключении от источника питания не сохраняет значения данных. Внешняя память – диски, флеш – в сто тысяч раз медленнее оперативной памяти, но существенно превосходит ее по объему, от сотен гигабайт до терабайтов, обеспечивая сохранность хранимых в ней данных.
- Машинный код представляет систему команд компьютера – операции нижнего уровня, непосредственно выполняемые компьютером, – вычисления над операндами в регистрах, обмен данными между разными уровнями памяти, передачи управления командам.
- Для компьютерной индустрии характерен экспоненциальный рост, известный как закон Мура. Поддержание этой тенденции потребовало перехода к многоядерным процессорам и параллельному программированию.
Новый словарь
| Address | Адрес | Bit | Бит |
| Byte | Байт | Core | Ядро (Первичная память) |
| Disk | Диск | Flash memory | Флеш-память |
| Giga | Гига | Hexadecimal | Шестнадцатеричный |
| Kilo | Кило | Mega | Мега |
| Moore's law | Закон Мура | Multicore (and manycore) | Многоядерный |
| Octal | Восьмеричный | Persistent | Живучий (сохраняемый) |
| RAM | RAM-память прямого доступа | Read | Чтение |
| Register | Регистр | Removable memory | Сменная память |
| Primary memory | Первичная (оперативная) память | Secondary memory | Вторичная память |
| Storage | Хранилище | Transient | Кратковременный |
| Word | Слово | Write | Запись |
1.7. Упражнения
1.7.1. Словарь
Дайте точные определения терминам словаря.
1.7.2. Карта концепций
Добавьте новые термины в карту концепций, построенную в предыдущих лекциях.
1.7.3 Измерения
Сколько байтов в:
- килобайте
- мегабайте
- мегаслове (слово = 4 байта)
- гигабайте?
1.7.4. Ваш новый лэптоп
Каталог рекламирует лэптоп с 1,3 GB памяти.
- Сколько байтов содержит эта память?
- Сколько битов содержит эта память?
- Предположим, что вся память используется для представления одной переменной. Сколько возможных значений может иметь эта переменная? Не требуется выписать точное число (подсказка: не пытайтесь это сделать, если только вы не являетесь владельцем бумажной фабрики; приведите аппроксимацию в форме
 ).
). - Если бы вы захотели написать это число на бумаге, 100 цифр в строке и 60 строк на странице, то сколько страниц вам бы потребовалось?
1.7.5. Размер и скорость передачи
Необходимо передать 128 MB данных, используя 128 Mb модем, работающий с максимальной скоростью. Сколько секунд это займет?
1.7.6. Восьмеричная арифметика
Восьмеричная арифметика использует систему с основанием 8 и цифрами от 0 до 7.
- Запишите десятичное число 300000 в восьмеричной системе.
- Число 74223 в восьмеричной системе запишите как десятичное число.
- Вычислите сумму этих двух чисел, используя восьмеричную арифметику. Представьте результат в обеих системах.
1.7.7. Шестнадцатеричная арифметика
Шестнадцатеричная арифметика использует систему с основанием 16 и цифрами от 0 до 9 и A до F.
- Запишите десятичное число 300000 в шестнадцатеричной системе.
- Число A42D3 в шестнадцатеричной системе запишите как десятичное число.
- Вычислите сумму этих двух чисел, используя шестнадцатеричную арифметику. Представьте результат в обеих системах.


