Рекурсия и деревья
8.2. Ханойская башня
В величественном храме Бенареса, под куполом, отмечающим центр мира, на медной плите установлены три бриллиантовых стержня. Каждый стержень высотой в локоть и тонок, как пчелиная талия. На один из этих стержней в начале мироздания Бог поместил 64 диска из чистого золота. Самый большой диск покоится на медной плите, а остальные, друг друга меньше, создают пирамиду, вздымающуюся к вершине стержня. Это и есть священная башня Брахмы.
Ночью и днем неустанно священники, сменяя друг друга, работают, чтобы перенести священную башню на третий бриллиантовый стержень, не нарушив при этом священных правил, установленных Брахмой. Когда их работа будет закончена, падет башня, падут брахманы и наступит конец мира.
Несмотря на восточный орнамент, эта история является созданием французского математика Эдуарда Лукаса (подписывающегося как "N. Claus de Siam" – анаграмма "Lucas d'Amiens", с добавлением названия его родного города). На рынке в Таиланде (Сиам) я купил подобную башню, показанную на рисунке. Метки А, В, С – это мое добавление. Не буду распространяться на тему, почему я выбрал модель, сделанную из дерева, а не из бриллиантов, золота и меди. Но вполне законно спросить, почему на ней только 9 дисков, хотя портфель у меня был большой и мог бы вместить башню из 64 дисков.
Время теста!
Почему коммерчески доступные модели Ханойской башни имеют размеры много меньшие, чем 64 диска?
(Подсказка: игра сопровождается бумажным свертком, на котором дается решение головоломки в форме последовательности ходов; А => C, A => B и т. д.)
Чтобы ответить на этот вопрос, давайте оценим минимальное число ходов 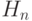 (ход – это перемещение диска с одного стержня на другой), требуемое для решения задачи. Если задача имеет решение, то нужно перенести n дисков со стержня А на стержень В, используя стержень С как промежуточный. При этом нужно соблюдать правило Будды, запрещающее класть больший диск на меньший. В оригинальной версии n = 64, для небольшой модели n = 9.
(ход – это перемещение диска с одного стержня на другой), требуемое для решения задачи. Если задача имеет решение, то нужно перенести n дисков со стержня А на стержень В, используя стержень С как промежуточный. При этом нужно соблюдать правило Будды, запрещающее класть больший диск на меньший. В оригинальной версии n = 64, для небольшой модели n = 9.
Заметим, что для любой стратегии перемещения в некоторый момент необходимо перенести самый большой диск со стержня А на стержень В, а это возможно лишь при условии, что все остальные n -1 дисков в этом момент находятся на диске С в требуемом порядке:
Каково минимальное число ходов, необходимое для достижения этого промежуточного состояния? Необходимо перенести n -1 диск со стержня А на стержень С, не перемещая самый большой диск и используя стержень В как промежуточный. Ввиду симметричности задачи для этого потребуется  ходов.
ходов.
Сразу же по достижении этого состояния можно перенести за один ход самый большой диск с А на В, после чего перенести n – 1 диск с С на В, используя А как промежуточный. Общее количество ходов:

Учитывая, что  равно 0, получим:
равно 0, получим:

Как следствие, нетрудно получить ответ на наш тест. Вспомним, что  , или примерно
, или примерно  , и получим, что число ходов
, и получим, что число ходов 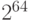 примерно равно
примерно равно  .
.
Год – это примерно 30 миллионов секунд. Если предположить, что священники Бенареса за секунду выполняют один ход – весьма неплохая скорость для переноса золотого диска, – всю работу они закончат за 500 миллиардов лет, что примерно в 30 раз превосходит оценочный возраст существования нашей вселенной. Даже компьютеру, выполняющему 100 миллионов ходов за секунду, при моделировании этой задачи для переноса дисков потребуется не одна тысяча лет.
Вывод оценки 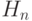 был конструктивным, в том смысле, что он дает практическую стратегию для перемещения дисков.
был конструктивным, в том смысле, что он дает практическую стратегию для перемещения дисков.
- Переместить
 диск с А на С, используя В как промежуточное хранилище и руководствуясь правилами игры.
диск с А на С, используя В как промежуточное хранилище и руководствуясь правилами игры. - После этого стержень В будет пуст, а на А будет находиться только один самый большой диск, который и переносится за один ход с А на В. Этот ход соответствует всем правилам игры – перенос одного диска с вершины одного стержня на другой стержень, в вершине которого нет диска, размер коего меньше размера переносимого диска.
- После этого переместить
 диск с С на В, используя А как промежуточное хранилище, руководствуясь правилами игры. Самый большой диск, находящийся на В, не мешает переносу дисков меньшего размера.
диск с С на В, используя А как промежуточное хранилище, руководствуясь правилами игры. Самый большой диск, находящийся на В, не мешает переносу дисков меньшего размера.
Эта стратегия превращает число ходов  из теоретического минимума в практически достижимую цель. Мы можем записать алгоритм в виде рекурсивной процедуры, входящей в класс NEEDLES:
из теоретического минимума в практически достижимую цель. Мы можем записать алгоритм в виде рекурсивной процедуры, входящей в класс NEEDLES:
hanoi (n: INTEGER; source, target, other: CHARACTER)
— Перенос n дисков из source на target,
— используя other как промежуточное хранилище,
— в соответствии с правилами игры "Ханойская башня"
require
non_negative: n >= 0
different1: source /= target
different2: target /= other
different3: source /= other
do
if n > 0 then
hanoi (n–1, source, other, target)
move (source, target)
hanoi (n–1, other, target, source)
end
end
По соглашению стержни представляются символами – 'A', 'B', 'C'. Другое соглашение, принятое в этой лекции (уже использованное в предыдущих примерах), состоит в подсветке рекурсивных ветвей кода, – процедура hanoi содержит два таких участка.
Базисная операция move(source, target) перемещает один диск с вершины стержня source на вершину target. Предусловие устанавливает, что на source должен находиться, по крайней мере, один диск, а на target диска либо нет, либо диск в вершине имеет больший размер, чем перемещаемый диск. Запишем move как процедуру, выводящую на консоль инструкцию по перемещению диска:
move (source, target: CHARACTER)
— Инструкция по перемещению диска с source на target.
do
io.put_character (source)
io.put_string (" to ")
io.put_character (target)
io.put_new_line
end
Время программирования!
Напишите систему с корневым классом NEEDLES, включающим процедуры hanoi и move. Проверьте их работоспособность на примерах.
Например, выполните вызов
hanoi (4, 'A', 'B', 'C')
В результате должна быть напечатана последовательность из пятнадцати ( ) ходов:
) ходов:
| A на C | B на C | B на A |
| A на B | A на C | C на B |
| C на B | A на B | A на C |
| A на C | C на B | A на B |
| B на A | C на A | C на B |
Эта последовательность ходов успешно переносит диски с А на B в полном соответствии с правилами игры.
Один из способов анализа рекурсивного решения – процедуры hanoi – состоит в том, чтобы рассматривать перемещение n – 1 дисков, как один обобщенный ход. В этом случае мы могли бы начать перемещение с этого хода (с А на С):
После этого можно сделать обычный ход, перенеся самый большой диск на целевой стержень, а затем снова выполнить обобщенный ход, который легален, поскольку все диски обобщенного хода меньше, чем диск, уже лежащий на целевом стержне.
Конечно, это фиктивное рассмотрение, поскольку правилами разрешается перенос только одного диска за один ход, но перемещая n – 1 диск, можно применять ту же технику, зная, что целевой стержень либо пуст, либо содержит диски большего размера. Так можно рекурсивно выполнять перемещения, уменьшая каждый раз значение n. Когда же n становится равным нулю, то делать ничего не нужно.
Не стоит легкомысленно относиться к примеру с Ханойской башней. Это решение служит прекрасной моделью для многих рекурсивных программ с важными практическими приложениями. Простота алгоритма является результатом использования двух рекурсивных вызовов, и это делает эту задачу идеальной для изучения свойств рекурсивных алгоритмов, к чему мы вернемся чуть позже в этой лекции.



