Рекурсия и деревья

Дети и родители

Дети (непосредственные потомки) узла – сами узлы – являются корневыми узлами левого и правого поддеревьев:

Рис. 8.11. Бинарное дерево (представление "ветвлением")

Если С – сыновний (дочерний) узел В, то В – родитель С. Более точно мы можем сказать, что В является "родителем" С, благодаря следующему результату:

Теорема: "Единственный родитель"

Теорема кажется очевидной, но мы докажем ее, что даст нам возможность познакомиться с рекурсивными доказательствами.

Рекурсивные доказательства

Рекурсивное доказательство теоремы о единственном родителе в значительной степени отражает рекурсивное определение бинарного дерева.

Если бинарное дерево BT пусто, то теорема выполняется. В противном случае бинарное дерево имеет корень и два непересекающихся бинарных дерева, о которых мы можем предположить – "рекурсивная предпосылка", – что они оба удовлетворяют теореме. Это следует из определений "бинарного дерева", "ребенка" и "родителя", так что узел С может иметь родителя Р в ВТ только одним из трех возможных случаев:

В случае Р1 узел С по гипотезе рекурсивности, являясь корнем, не имеет родителей в своем поддереве, так что у него есть единственный родитель – корень всего дерева ВТ. В случаях Р2 и Р3, опять-таки по гипотезе рекурсивности, Р был единственным родителем С в соответствующем поддереве, и это остается верным и во всем дереве.

Любой узел С, отличный от корня, удовлетворяет одному из трех рассмотренных вариантов и, следовательно, имеет в точности одного родителя. Только если С является корнем дерева, он не будет соответствовать рассмотренным ситуациям и, как следствие, у него не будет родителей, что и завершает доказательство теоремы.

Подобные рекурсивные доказательства полезны, когда необходимо установить, что некоторое свойство выполняется для всех экземпляров рекурсивно определенного понятия. Структура доказательства определяется структурой определения.

• Для любой нерекурсивной ветви определения необходимо доказать свойство непосредственно (в примере нерекурсивной ветвью является пустое дерево).
• Для рекурсивной ветви определяется новый экземпляр понятия в терминах существующих экземпляров. Для них можно предположить, что свойство выполняется (это и есть "гипотеза рекурсивности"), после чего требуется доказать, что при этих предположениях свойство выполняется.

Эта схема применима в целом для всех рекурсивно определяемых понятий. Мы увидим ее применение к рекурсивно определенной процедуре hanoi.

Бинарные деревья выполнения

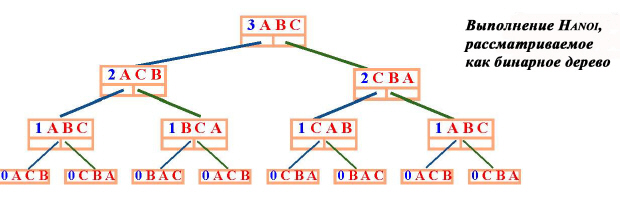
Интересный пример бинарного дерева можно получить, моделируя выполнение процедуры hanoi, например, для трех дисков. Каждый узел содержит аргументы данного вызова, а левое и правое поддерево соответствуют рекурсивным вызовам:

Рис. 8.12. Выполнение Hanoi, рассматриваемое как бинарное дерево

Добавление операции move позволило бы реконструировать последовательность операций. Формально мы выполним это позднее.

Этот пример высвечивает связь межу рекурсивными алгоритмами и рекурсивными структурами данных. Для методов, число рекурсивных вызовов в которых задавалось переменной, а не равнялось двум, как в hanoi, выполнение моделировалось бы не бинарным деревом, а деревом общего вида.

Еще о свойствах бинарных деревьях и о терминологии

Как отмечалось, узел бинарного дерева может иметь:

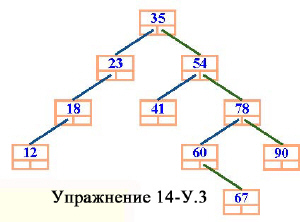
• как левого, так и правого сына, подобно узлу 35 из нашего примера;
• только левого сына, подобно всем узлам левого поддерева, помеченным значениями 23, 18, 12;
• только правого сына, подобно узлу 60;
• не иметь сыновних узлов. Такие узлы называются листьями дерева; в примере листьями являются узлы с пометками 12, 41, 67 и 90.

Рис. 8.13. Копия ранее приведенного дерева

Определим восходящий путь в бинарном дереве как последовательность из нуля или более узлов, где любой узел последовательности является родителем предыдущего узла, если таковой имеется. В нашем примере узлы с метками 60, 78, 54 формируют восходящий путь. Справедливо следующее свойство, являющееся следствием теоремы о единственном родителе.

Теорема: "Путь к корню"

Доказательство. Рассмотрим произвольный узел С бинарного дерева. Построим восходящий путь, начинающийся в С. В соответствии с теоремой о единственном родителе такой путь определяется единственным образом. Если путь конечен, то заканчиваться он должен в корне дерева, поскольку любой другой узел имеет родителя, и следовательно, построение восходящего пути могло бы быть продолжено. Для завершения доказательства необходимо показать, что все пути конечны. Единственный способ построения бесконечного пути (учитывая, что число узлов бинарного дерева по определению конечно) состоит в том, что путь включает цикл. Если некоторый узел n встретится дважды, то он встретится сколь угодно много раз, так что бесконечный путь должен содержать подпоследовательность в форме n... n. Но это означает, что n появляется в своем собственном левом или правом поддереве, что невозможно по определению бинарных деревьев.

Рассмотрение нисходящих путей позволяет установить следующий факт, как следствие предыдущей теоремы.

Теорема: "Нисходящий путь"

Весом бинарного дерева является максимальное число узлов среди всех нисходящих путей от корня к листьям дерева. В примере вес бинарного дерева равен 5, он достигается на пути, который ведет от корня к листу, помеченному как 67.

Это понятие можно определить рекурсивно, следуя снова рекурсивной структуре определения. Вес пустого дерева равен нулю. Вес непустого дерева равен 1 плюс максимум (рекурсивно) из весов левого и правого поддеревьев. Мы можем добавить соответствующую функцию в класс BINARY_TREE:

height: INTEGER
        — Максимальное число узлов нисходящего пути.
    local
        lh, rh: INTEGER
    do
        if left /= Void then lh := left.height end
        if right /= Void then rh := right.height end
        Result := 1 + lh.max (rh)
    end
        

Здесь рекурсивное определение адаптируется к соглашению, принятому для класса, который рассматривает только непустые поддеревья. Отметьте опять-таки схожесть с hanoi.

Операции над бинарными деревьями

В классе BINARY_TREE пока определены только три компонента, все они являются запросами: item, left и right. Мы можем добавить процедуру создания:

    make (x: G)
            — Инициализация item значением x.
        do
            item := x
        ensure
            set: item = x
        end
Добавим в класс команды, позволяющие изменять поддеревья, и значение в корне:
    add_left (x: G)
            — Создать левого сына со значением x..
        require
            no_left_child_behind: left = Void
        do
            create left.make (x)
        end
    add_right … Аналогично add_left…
    replace (x: G)
            — Установить значение корня равным x.
        do item := x end
        

На практике удобно специфицировать replace как команду-присваиватель для соответствующего запроса, изменив объявление запроса следующим образом:

item: G assign replace
        

Это позволяет писать bt.item:= x вместо bt.item.replace(x).

Обходы бинарного дерева

Нет ничего удивительного в том, что, благодаря рекурсивной определенности, с бинарным деревом связываются многие рекурсивные методы. Функция height является одним из таких примеров. Приведем сейчас и другие. Предположим, что требуется напечатать все значения элементов, связанных с узлами дерева. Следующая процедура, добавленная в класс, выполняет эту работу:

print_all
        — Печать значений всех узлов.
    do
        if left /= Void then print_all (left)end
        print (item)
        if right /= Void then print_all (right) end
    end
        

Заметьте, структура print_all идентична структуре hanoi.

Хотя роль процедуры print_all состоит в печати всех значений, ее алгоритмическая схема не зависит от специфики операции, выполняемой над узлами дерева (print в данном случае). Процедура является примером обхода бинарного дерева: алгоритма, выполняющего однократно некоторую операцию над каждым элементом структуры данных в некотором заранее предписанном порядке обхода узлов. Обход является вариантом итерации.

Для двоичных деревьев наиболее часто используются три порядка обхода дерева, которые иногда называют соответственно инфиксным, префиксным и постфиксным порядками обхода.

Порядки обхода бинарного дерева

В этих определениях "посетить" означает выполнение операции над отдельным узлом, такой как print в процедуре print_all; "обход" означает либо рекурсивное применение алгоритма для поддерева, либо отсутствие каких-либо действий, если поддерево пусто.

Префиксный порядок обхода, так же как и другие способы обхода, идущие, насколько это возможно, в глубину поддерева, называются также обходами "вначале в глубину", например, "самый левый в глубину".

Процедура print_all является иллюстрацией инфиксного способа обхода дерева. Достаточно просто записываются и другие способы обхода, например, для постфиксного обхода тело процедуры post имеет вид:

if left /= Void then post (left) end
if right /= Void then post (right) end
visit (item)
        

Здесь visit является операцией над узлом, такой как print.

В качестве еще одной иллюстрации инфиксного обхода рассмотрим снова бинарное дерево выполнения hanoi для n = 3, где узлы уровня 0 опущены, поскольку не представляют интересной информации в данном случае.

Рис. 8.14. Выполнение Hanoi в инфиксном порядке обхода

Процедура hanoi является матерью всех инфиксных обходов: обход левого дерева, если оно есть, посещение корня, обход правого поддерева, если оно есть. При посещении каждого узла выполняется операция move(source, target). Инфиксный порядок дает нужную последовательность ходов: A B, A C, B C, A B, C A, C B, A B.

Бинарные деревья поиска

Для произвольного бинарного дерева процедура print_all, реализующая инфиксный порядок, печатает значения узлов в произвольном порядке. Если же порядок важен для нас, то необходимо переходить к бинарным деревьям поиска.

Множество G, над которым определено общее бинарное дерево, может быть любым множеством. Для бинарных деревьев поиска предполагается, что на множестве G задано полное отношение порядка, позволяющее сравнивать любые два элемента G, задавая булевское выражение a < b, такое, что истинно одно из трех отношений: a < b, b < a, a ∼ b. Примерами таких множеств могут служить INTEGER и REAL с отношением порядка <, но G может быть любым вполне упорядоченным множеством.

Как обычно, мы пишем a < = b, когда либо a < b, либо a ∼ b. Аналогично, b > a, если a < b. Над вполне упорядоченным множеством можно определить бинарное дерево поиска.

Определение: бинарное дерево поиска

Значения в узлах левого поддерева меньше значения в корне, а в правом поддереве – больше. Это свойство применимо не только ко всему дереву в целом, но, рекурсивно, к любому поддереву, прямому или непрямому потомку корня. Это свойство будем называть инвариантом бинарного дерева поиска.

Рис. 8.15. Упражнение 5.11.3

Дерево, показанное на рисунке, является бинарным деревом поиска.

Процедура print_all, примененная к этому дереву, напечатает значения, упорядоченные по возрастанию, начиная с наименьшего значения 12.

Время программирования!

Производительность

Давайте рассмотрим причины, по которым деревья поиска являются полезными, как контейнерные структуры – потенциальные соперники хэш-таблиц. В самом деле, они обычно обеспечивают лучшую производительность, чем последовательные списки. В предположении случайного характера появления данных последовательный список, содержащий n элементов, обеспечивает:

• O(1) вставку (если элементы сохраняются в порядке вставки);
• O(n) для поиска.

Для бинарного дерева поиска обе операции имеют сложность O(log n), что намного лучше, чем O(n) для больших n (вспомните, что для нотации "О-большое" не имеет значения основание алгоритма). Проанализируем эффективность работы полного бинарного дерева, которое определяется тем, что для любого его узла оба поддерева, выходящие из узла, имеют одну и ту же высоту h:

Рис. 8.16. Полное бинарное дерево

Нетрудно видеть, при помощи индукции по высоте h, что число узлов n в полном дереве высоты h равно 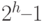. Как следствие, . В полном дереве как поиск, так и вставка, используя приведенные ниже алгоритмы, выполняются за время O(log n), начиная работу в корне и следуя нисходящим путем к листьям дерева. В этом и состоит главная привлекательность бинарных деревьев поиска.

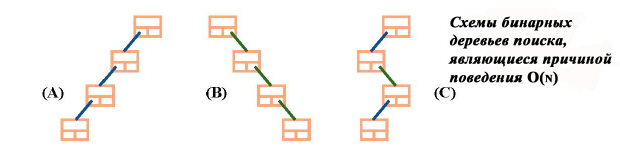
Конечно, большинство практических бинарных деревьев не являются полными. Если не повезет при вставке, то производительность может быть столь же плоха, как и для последовательного списка – O(n). К этому добавляются потери памяти, связанные с необходимостью хранения двух ссылок для каждого узла, в то время как для списка достаточно одной ссылки. На следующем рисунке показаны варианты "плохих" деревьев поиска:

Рис. 8.17. Схемы бинарных деревьев поиска, являющиеся причиной поведения O(N)

При случайном порядке вставки бинарные деревья поиска остаются достаточно близкими к полным деревьям с поведением близким к O(log n). Можно гарантировать выполнение операций поиска, вставки и удаления за время O(log n), если пользоваться специальными вариантами таких деревьев – АВЛ-деревьями или черно-красными деревьями, которые являются почти полными деревьями.