Кривые и поверхности в компьютерной геометрии, II
Поверхности, затягивающие заданные граничные контуры
В ряде приложений (например, в проектировании корпусов и крыльев самолетов и кораблей) требуется строить гладкие поверхности, затягивающие заданные остовы из кривых - криволинейные сетки, криволинейные направляющие (например, несущий остов корпуса корабля), различные граничные контуры. Во многих случаях важное значение имеет также и вычислительная сторона вопроса - сложность вычисления радиус-вектора поверхности и ее дифференциально-геометрических характеристик не должна быть слишком высокой.
В компьютерной геометрии существует несколько различных подходов к решению подобных задач. Ниже будет рассмотрены некоторые из этих подходов, ставшие классическими.
Линейчатые поверхности
Линейчатая поверхность - геометрическое место точек отрезков прямых, соединяющих соответствующие друг другу точки двух заданных кривых. Пусть  и
и  - две заданные кривые. Тогда определяемая ими линейчатая поверхность имеет вид
- две заданные кривые. Тогда определяемая ими линейчатая поверхность имеет вид

где 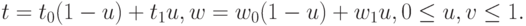
Если обе кривые 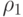 и
и 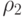 замкнуты, то линейчатая поверхность замкнута по u. По параметру v линейчатая поверхность всегда незамкнута.
замкнуты, то линейчатая поверхность замкнута по u. По параметру v линейчатая поверхность всегда незамкнута.
Если обе кривые 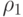 и
и 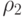 - отрезки прямых, то линейчатая поверхность называется билинейной и определяется только своими четырьмя угловыми точками
- отрезки прямых, то линейчатая поверхность называется билинейной и определяется только своими четырьмя угловыми точками  :
:
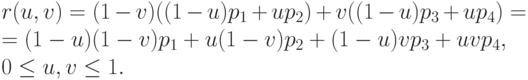
Секториальные поверхности
Секториальная поверхность - частный случай линейчатой поверхности, когда одна из кривых 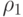 и
и 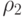 вырождается в точку:
вырождается в точку:

где 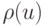 - кривая, p - точка,
- кривая, p - точка, 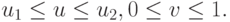
Секториальная билинейная поверхность называется треугольной поверхностью.
Поверхности Кунса
Линейные поверхности Кунса. Вычтем и добавим к уравнению линейчатой поверхности уравнение билинейной поверхности, построенной по четырем угловым точкам (см. выше). Уравнение линейчатой поверхности примет вид
 |
( 6.13) |
где  и
и  - кривые, по которым строится данная линейчатая поверхность, причем считается, что на них обеих задан один и тот же параметр
- кривые, по которым строится данная линейчатая поверхность, причем считается, что на них обеих задан один и тот же параметр  и
и
 |
( 6.14) |
- отрезки прямых.
Подставим теперь в уравнение (6.13) вместо отрезков прямых (6.14) уравнения двух произвольных кривых 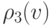 и
и  соединяющих соответственно пары точек
соединяющих соответственно пары точек 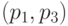 и
и  Тогда новая поверхность, задаваемая уравнением (6.13), будет определяться четырьмя кривыми
Тогда новая поверхность, задаваемая уравнением (6.13), будет определяться четырьмя кривыми 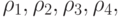 образующими криволинейный четырехугольник, натянутый на угловые точки
образующими криволинейный четырехугольник, натянутый на угловые точки  При этом все четыре кривые
При этом все четыре кривые 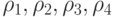 войдут в уравнение (6.13) симметрично. Получится линейная поверхность Кунса.
войдут в уравнение (6.13) симметрично. Получится линейная поверхность Кунса.
Определение 6.3.1. Пусть заданы четыре кривые, образующие криволинейный четырехугольник с углами в точках  :
:

Обозначим

Функции 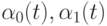 будем называть функциями смещения линейной поверхности Кунса. Сама линейная поверхность Кунса определяется следующей формулой:
будем называть функциями смещения линейной поверхности Кунса. Сама линейная поверхность Кунса определяется следующей формулой:
 |
( 6.15) |
Замечание 6.3.1. Линейная поверхность Кунса не является, вообще говоря, линейчатой поверхностью. Название "линейная" обусловлено тем, что в ее определении используются линейные функции смещения 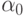 и
и 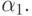
Замечание 6.3.2. Параметрическая область поверхности Кунса может иметь вид прямоугольника, не обязательно совпадающего с квадратом ![[0,1] \times [0,1] .](/sites/default/files/tex_cache/1ce45fc7e3991423236d4a7f34ace048.png)
Матричный вид уравнения поверхности Кунса. Преобразуем формулу (6.15) к другому виду. Имеем в матричных обозначениях
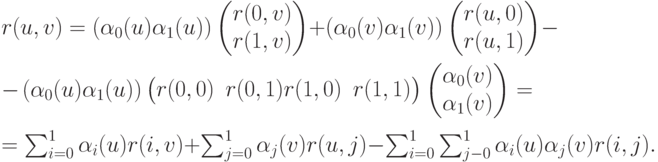
Пример 6.3.1. Зададим с помощью поверхности Кунса область D плоскости, ограниченную эллипсом 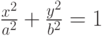 или
или 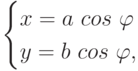 где
где  с полуосями
с полуосями 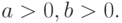 Представим границу области D в виде четырех кривых - дуг эллипса, стыкующихся в точках
Представим границу области D в виде четырех кривых - дуг эллипса, стыкующихся в точках  Соответствующая линейная поверхность Кунса имеет вид
Соответствующая линейная поверхность Кунса имеет вид

Преимущество задания плоских областей в виде линейных поверхностей Кунса состоит в том, что у поверхности Кунса параметрическая область -всегда прямоугольник.
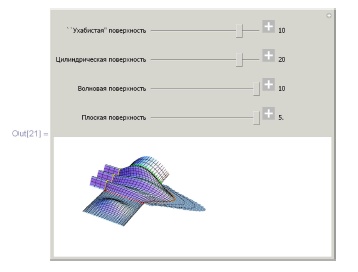
Пример 6.3.2. Поверхность Кунса, построенная по кривым, лежащим на заданных поверхностях. Кривые раскрашены красным, зеленым, желтым и оранжевым.
In[21]: =
DynamicModule[{rl = 30 . , r2 = 30. , r3 = 30 . , d = 50 . , u , v, ml, m2 , m3, m4 , fl,
f2, f3, f4, rfel, ?, MV, MU, laml, lam2, rfk}, rl = 30. ; r2 = 30. ; r3 = 30. ;
d = 50. ; laml = 2. ; lam2 = 1. ;
f1 [ml_] : = {rl - rl *Cos[u * Pi] , laml * d* v / 2, m1* (Sin [u * Pi] *Sin[v*Pi])^4} ;
f2 [m2_ ] := {r2 - r2 *Cos[u*Pi] , d- lam2 *d/ 2 + lam2 *d*v/2, m2* (Sin [u* Pi])^2};
f3[m3_ ] := {0.8 * r3*u, d*v, m1* (Sin[v* 3* Pi] )^2} :
f4 [m4_] :={1.6*r1+0.4*rl*u+(v^4-2*v^3+v^2)*100*m4*u, d*v, 0} ;
Manipulate[
Show[{ParametricPlot3D[Evaluate@fl [ml] , {u, 0, 1}, {v, -1, 0}, Mesh -> {24, 24},
PlotRange -> All] ,
ParametricPlot3D[Evaluate@{fl [ml] /. v -> 0}, {u, 0, 1}, Mesh -> {24, 24),
PlotRange -> All, PlotStyle -> {Red} ] ,
ParametricPlot3D[Evaluate@f2[m2] , {u , 0, 1}, {v, 1, 2} , Mesh -> {24, 2},
PlotRange -> All] ,
ParametricPlot3D[Evaluate@{f2 [m2] /. v -> l}, {u, 0, 1}, Mesh -> {24, 24},
PlotRange -> All, PlotStyle -> {Green} ] ,
ParametricPlot3D[Evaiuate@f3[m3] , {u, -1, 0}, {v, 0, 1}, Mesh -> {2, 24},
PlotRange -> All] ,
ParametricPlot3D[Evaluate@{f3 [m3] /.u -> 0), {v, 0, 1}, Mesh -> {24, 24},
PlotRange -> All, PlotStyle -> {Yellow} ] ,
ParametricPlot3D[Evaluate@f4 [m4] , {u, 1, 2}, {v, 0, 1}, Mesh -> {2, 24},
PlotRange -> All] ,
ParametricPlot3D[Evaluate@{f4 [m4] /.u -> l}, {v, 0, 1}, Mesh -> {24, 24},
PlotRange -> All, PlotStyle -> {Orange} ] ,
ParametricPlot3D [Evaluate@rfel [ml, m2, m3, m4], {u, 0, 1}, {v, 0, 1},
Mesh -> {24 , 24} , PlotRange -> All] } ,
ImageSize -> {500 , 380}, Axes -> None, Boxed -> False,
PlotRange -> {{-30, 135}, {-50, 100}, {-30, 30}}
], {{ml, 10, " ' ' Ухабистая' ' поверхность"}, -15., 15., Appearance -> "Labeled"},
{{m2, 20, "Цилиндрическая поверхность"}, -30, 30, Appearance -> "Labeled"},
{{m3, 10, "Волновая поверхность"}, -10, 10, Appearance -> "Labeled"},
{{m4, 1, "Плоская поверхность"}, -5, 5, Appearance -> "Labeled"},
ControlPlacement -> Top,
Initialization : -> (
rl = 30 . ; r2 = 30. ; r3 = 30. ; d = 50. ; laml = 2. , lam2 = 1. ;
fl [ml_] : = {rl - rl *Cos [u * Pi] , laml *d*v/2, m1* (Sin[u * Pi] * Sin[v* Pi])^4} ;
f2[m2_] := {r2 - r2*Cos[u*Pi] , d- lam2*d/ 2 + lam2 *d*v/2, m2* (Sin[u*Pi] )^2} ;
f3[m3_] := {0.8 * r3*u, d*v, m3* (Sin[v* 3* Pi])^2} ;
f4 [m4_] :={1.6*rl+0.4*rl*u+(v^4-2*v^3+v^2)*100*m4*u, d*v, 0} ;
\alpha [t_] := t; MV[v_] : = {1 - \alpha [v] , \alpha [v] } ; MU[u_]: = {1 - \alpha [u] , \alpha [u] } ;
(* наши функции а *)
Table [rfk [ml, m2, m3, m4] [i] , {i, 3}] ;
Do[rfk[ml_, m2_, тЗ_, т4_] [i] =
MU[u].{f3[m3][[i]] /. u ->0, f4[m4][[i]] /. u ->l} +
MV[v] . {fl [ml] [ [i] ] /. v->0, f2[m2][[i]] /. V->1} -
MU[u] . {{f3[m3] [[i]] /. {u ->0, v-> 0} , f3[m3] [[i]] /. {u -> 0, v->l}},
{f4 [m4] [ [i] ] /. {u -> 1 , v-> 0} , f4 [m4] [ [i] ] /. {u-> 1, v -> 1} } } .MV[v] //
Together;
, {i, 3}] ; rfel[ml_, m2_, тЗ_, m4_] =
{rfk [ml, m2, m3, m4] [1] , rfk [ml, m2, m3, m4] [2] , rfk [ml, m2, m3, m4] [3] };) ]]Обобщенные поверхности Кунса. При стыковке линейных поверхностей Кунса по граничным кривым производные в направлении, ортогональном границе, претерпевают разрыв. Чтобы гладко склеивать поверхности Кунса, необходимо строить их таким образом, чтобы они имели на границе заданные (согласованные) производные до k -го порядка включительно. Производные в касательном направлении определяются уравнениями самих граничных кривых, а производные в трансверсальном к границе направлении необходимо задавать дополнительно.
Определение 6.3.2. Обобщенной поверхностью Кунса n-го порядка называется поверхность
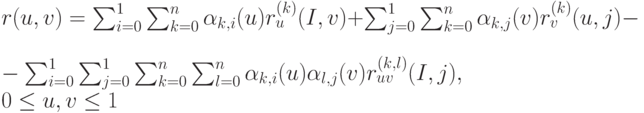 |
( 6.16) |
задаваемая четырьмя граничными кривыми 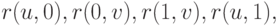 стыкующимися в точках
стыкующимися в точках  и
и 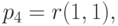 а также чистыми частными производными в трансверсальном направлении на граничных кривых до
а также чистыми частными производными в трансверсальном направлении на граничных кривых до  -го порядка включительно и смешанными частными производными в угловых точках
-го порядка включительно и смешанными частными производными в угловых точках  до
до  -го порядка включительно:
-го порядка включительно:
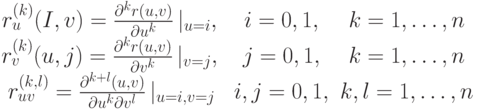 |
( 6.17) |
а также обобщенными функциями смещения  где
где  в качестве которых могут быть взяты произвольные гладкие функции, удовлетворяющие соотношениям
в качестве которых могут быть взяты произвольные гладкие функции, удовлетворяющие соотношениям
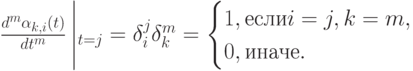 |
( 6.18) |
Здесь 
Задача 6.3.1. Проверить, что поверхность (6.16), определенная с помощью (6.17) и (6.18), имеет заданные в (6.17) производные на границе.
Замечание 6.3.3. В качестве обобщенных функций смещения всегда можно выбрать многочлены.
Пример 6.3.3. Определим функции смещения формулами
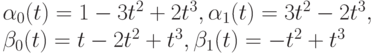 |
( 6.19) |
(здесь для простоты использованы обозначения  Пусть заданы , четыре кривые
Пусть заданы , четыре кривые 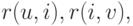 где
где  стыкующиеся в точках
стыкующиеся в точках  Пусть заданы первые производные на границе в трансверсальном направлении:
Пусть заданы первые производные на границе в трансверсальном направлении:  и вторые смешанные производные в угловых точках:
и вторые смешанные производные в угловых точках: 
Кубическая поверхность Кунса определяется формулой (в матричных обозначениях)
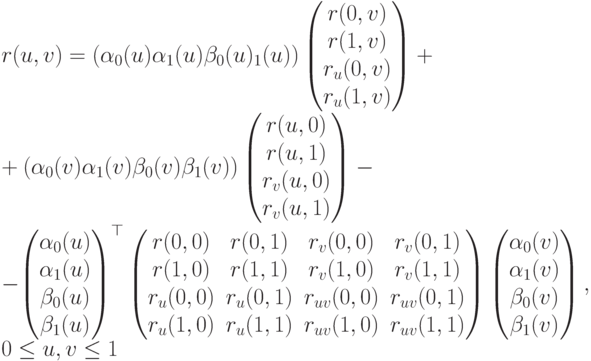
Задача 6.3.2. Написать на пакете Mathematica программу построения кубической поверхности Кунса.