Элементы управления и динамика
Задание вручную (переопределение заданных по умолчанию) элементов управления. Для этого в описании параметра нужно указать опцию ControlType ->¦ ТипУправления, где Тип Управления принимает одно из следующих значений: Animator, Checkbox, CheckboxBar, ColorSetter, ColorSlider, InputField, Manipulator, None, PopupMenu, RadioButton, RadioButtonBar, Setter, SetterBar, Slider, Slider2D, TogglerBar, Trigger, VerticalSlider:
In[83]: =
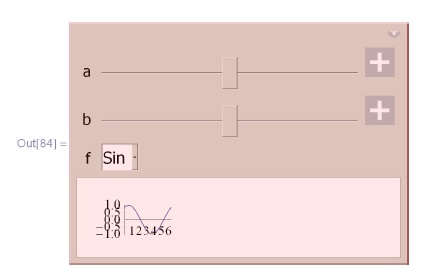
Manipulate [Plot [f [a x + b] g[x] , {x, 0,2 π },
PlotRange -> {{0, 2 π } , {-1, 1}}] ,
{{a, 1}, 0, 2},
{{b, 1}, 0, 2, 0.2},
{{f, Sin}, {Sin, Cos, Tan, Cot}, ControlType -> Slider} ,
{{g, Sin}, {Sin, Cos, Tan, Cot, Sqrt, Log},
ControlType -> RadioButton}
]
Такое переопределение не всегда удается. Скажем, здесь мы попытались задать дискретный набор значений переменной f с помощью двумерного слайдера:
In[84]:=
Manipulate [Plot [f [ах + b] , {х, 0, 2 π },
PlotRange -> {{0, 2 π } , {-1, 1}}] ,
{{а, 1}, 0, 2},
{{b, 1}, 0, 2, 0.2},
{{f, Sin}, {Sin, Cos, Tan, Cot}, ControlType -> SIider2D}
]Ничего хорошего не получилось, и возникло сообщение об ошибке:
Manipulate: :vstype :
ControlType ->Slider2D is not supported for the variable specification {f$$, {Sin, Cos, Tan, Cot}},
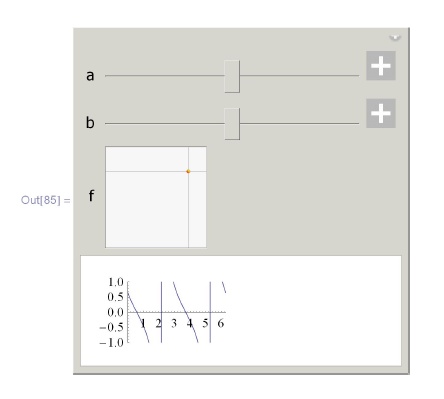
ControlType ->PopupMenu will be used instead. >>а панель Manipulate окрасилась в розовый цвет:
Использование функций в качестве элементов контроля.
In[85]:=Manipulate [Plot [f [ax + b] , {x, 0, 2 π } ,
PlotRange -> {{0, 2 π } , {-1, 1}}] ,
{{a, 1}, 0, 2},
{{b, 1}, 0, 2, 0.2},
{{f, Sin}, (Which[
pt[[1]] < 0.5 && pt[[2]] < 0.5, f = Sin,
pt[[1]] < 0.5 &&pt[[2]] >= 0.5, f = Cos,
pt[[1]] >= 0.5 &&pt[[2]] < 0.5, f = Tan,
pt[[1]] >= 0.5 &&pt[[2]] >= 0.5, f = Cot
] ; Slider2D[Dynamic[pt]]) & }
]
Интерактивное создание локаторов. Для этого в описании локатора нужно задать опцию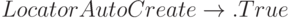 
. Теперь при удерживании клавиши Alt и клике на свободную часть поля мы будем создавать новые локаторы. При удерживании Alt и клике на существующий локатор мы удалим этот локатор:
In[86]:=
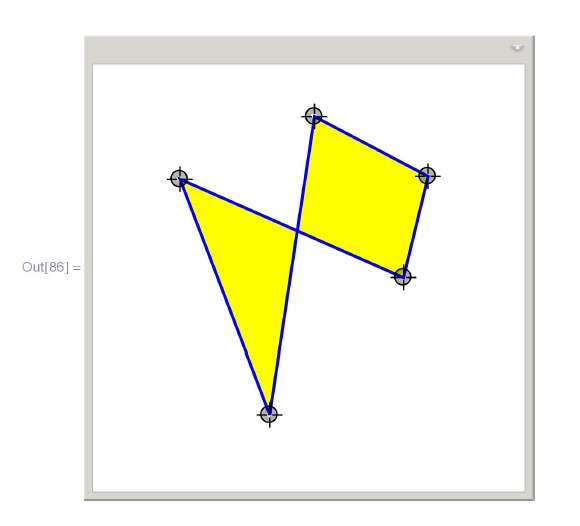
Manipulate[
Graphics[{EdgeForm[{Blue, Thick}], FaceForm[Yellow],
Polygon [pt]} , PlotRange -> 2] ,
{{pt, {{0, 0}, {1, 0}, {1, 1}, {0, 1}}}, Locator,
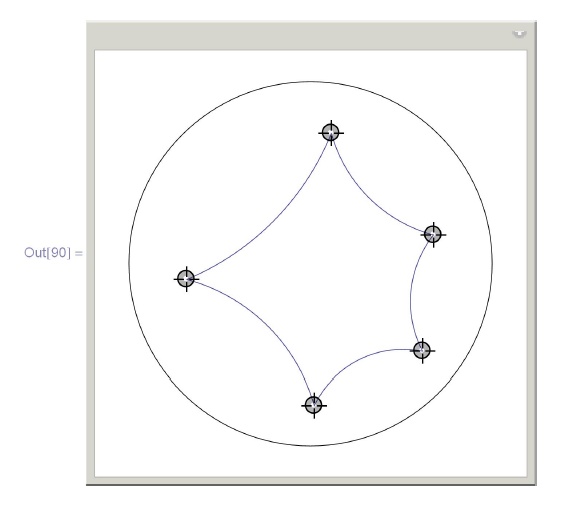
LocatorAutoCreate -> True} ]
Пример программы рисования многоугольника на плоскости Лобачевского ( Alt+Click на свободное поле добавляет вершины). Смещая локаторы, можно наблюдать за соответствующим изменением многоугольника:
![In[87]: = g[z_{-}, \varphi_{-} , z0_{-} ] :=e^{I \varphi} \frac{z-z0}{1-z Conjugate[z0]};\\
\begin{matrix}
&&givn[z_{-}, \varphi_{-}, z0_{-}]:=e^{-I \varphi}\frac{z_e^{I \varphi}z0}{1_ze^{-i \varphi}Conjugate[z0]};
\end{matrix}](/sites/default/files/tex_cache/d7da7437ebad2aebd238a969e124be91.png)
line[zl_, z2_, t_] : = ginv[tg [z2, 0, z1] , 0, zl] ;
Manipulate[res = p; Show[{
Graphics[Circle[]],
Table[ParametricPlot[
With[
{z = line [Complex [Sequence @@p[[i]] ] ,
Complex[Sequence @@
p[[If [i == Length [p] , 1, i + 1] ]] ] , t] },
{Re[z] , lm[z]}], {t, 0, 1}],
{i, If [Length [p] ==2, 1, Length [p] ]} ]
}], {{p, {{-1/2, 0}, {1/2, ?}}}, Locator,
LocatorAutoCreate -> True}
]