|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Обработка результатов имитационного эксперимента
5.8. Выявление несущественных факторов
Большое количество факторов усложняет и снижает эффективность эксперимента. Среди этого множества могут быть и несущественные факторы. Исключение их упростило бы эксперимент, не снижая его информативности.
Несущественный фактор выявляется так.
Выполняются первый эксперимент из  наблюдений с учетом проверяемого фактора и второй эксперимент также из
наблюдений с учетом проверяемого фактора и второй эксперимент также из  наблюдений - без него. В обоих случаях фиксируются отклики
наблюдений - без него. В обоих случаях фиксируются отклики  . Делается предположение, что обе выборки принадлежат одной генеральной совокупности, то есть, что проверяемый фактор - несущественный (это нулевая гипотеза). Дальнейшие рассуждения должны либо не опровергнуть эту гипотезу, либо посчитать ее недостаточно обоснованной.
. Делается предположение, что обе выборки принадлежат одной генеральной совокупности, то есть, что проверяемый фактор - несущественный (это нулевая гипотеза). Дальнейшие рассуждения должны либо не опровергнуть эту гипотезу, либо посчитать ее недостаточно обоснованной.
Итак, получены две последовательности откликов, в которой 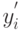 и
и 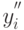 - значения откликов в
- значения откликов в 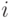 -м наблюдении при наличии и отсутствии проверяемого фактора соответственно:
-м наблюдении при наличии и отсутствии проверяемого фактора соответственно:
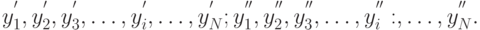
Согласно принятой гипотезе эти последовательности имеют одинаковые матожидания ![M[y]](/sites/default/files/tex_cache/3ca0262dc52b69660c0350dbff5551a5.png) и дисперсии
и дисперсии 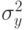 .
.
Рассмотрим случайную величину  , реализациями которой является последовательность случайных чисел
, реализациями которой является последовательность случайных чисел
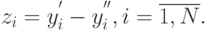
При независимости 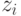 и достаточно большом числе наблюдений
и достаточно большом числе наблюдений  согласно центральной предельной теореме:
согласно центральной предельной теореме:
![M [\overline{z}] =M [ z ] = 0,\,\,\, \sigma_{\overline{z}} = \cfrac{\sigma_z}{\sqrt{N}}.](/sites/default/files/tex_cache/1782cd96b3f84d1c3a30f9dfa725b46d.png)
Очевидно:
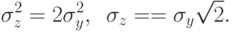
Как отделить случайные отклонения  от нуля от тех, которые мы будем считать не подтверждающими принятую гипотезу?
от нуля от тех, которые мы будем считать не подтверждающими принятую гипотезу?
Такое разделение осуществляется по следующему правилу: если вычисленная величина  окажется маловероятной, в рамках нормального распределения и данном среднеквадратическом отклонении
окажется маловероятной, в рамках нормального распределения и данном среднеквадратическом отклонении 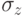 , то такое отклонение
, то такое отклонение  от нуля считается не соответствующим принятой гипотезе.
от нуля считается не соответствующим принятой гипотезе.
Эту малую вероятность называют уровнем значимости и обозначают 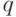 . Обычно
. Обычно  - в зависимости от степени опасности совершения ошибки первого или второго рода.
- в зависимости от степени опасности совершения ошибки первого или второго рода.
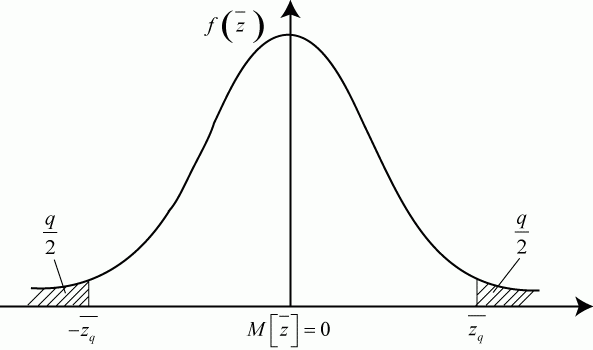
На графике плотности распределения 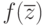 уровень значимости
уровень значимости 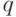 показан заштрихованным участком (рис. 5.4).
показан заштрихованным участком (рис. 5.4).
Для нормального закона распределения случайной величины  вероятность превышения
вероятность превышения  некоторого значения определяется известным выражением:
некоторого значения определяется известным выражением:

- граничное значение
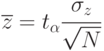
![[1-2\Phi(t_{\alpha})]=q](/sites/default/files/tex_cache/dc87c4d4d21013bdcd1fcfe0d782c131.png)
Аргумент функции Лапласа 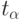 находим из соответствующего справочника согласно
находим из соответствующего справочника согласно 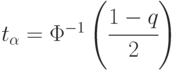 и, как было указано ранее,
и, как было указано ранее, 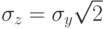
Из изложенного следует:
- если
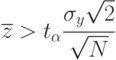 , принятая гипотеза о несущественности проверяемого фактора не подтверждается;
, принятая гипотеза о несущественности проверяемого фактора не подтверждается; - если
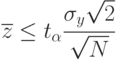 , принятая гипотеза не опровергается (в рамках принятого уровня значимости
, принятая гипотеза не опровергается (в рамках принятого уровня значимости 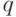 ).
).
Обычно величина 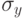 неизвестна, поэтому следует использовать ее оценку
неизвестна, поэтому следует использовать ее оценку 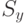 :
:
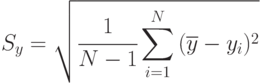
Оценку  и ряд значений
и ряд значений  можно получить из данных первого эксперимента (
можно получить из данных первого эксперимента ( 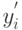 ) или второго (
) или второго ( 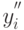 ), так как в силу рассматриваемой гипотезы они идентичны. Однако следует помнить, что если
), так как в силу рассматриваемой гипотезы они идентичны. Однако следует помнить, что если 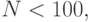 то вместо аргумента функции Лапласа
то вместо аргумента функции Лапласа 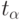 надо брать
надо брать 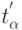 - аргумент функции Стьюдента.
- аргумент функции Стьюдента.
Пример 5.6. Исследуется зависимость времени пребывания заявки в системе массового обслуживания от дисциплины выборки заявок из очереди: LIFO или FIFO. Проведены два эксперимента. Первый эксперимент из 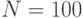 наблюдений с дисциплиной FIFO и второй эксперимент также из
наблюдений с дисциплиной FIFO и второй эксперимент также из 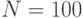 наблюдений с дисциплиной LIFO.
наблюдений с дисциплиной LIFO.
Решение
Выдвигается гипотеза о несущественности влияния на время пребывания заявки в системе массового обслуживания изменения дисциплины FIFO на LIFO.
Результаты измерений и вычислений:
-
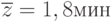 ,
, 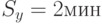 ;
; - для уровня значимости
 ,
, 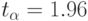
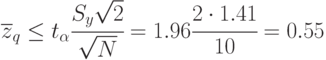
Так как  то гипотеза не подтверждается. Для времени пребывания заявки в очереди в системе массового обслуживания не безразлично, какая дисциплина выборки заявок из очереди применена.
то гипотеза не подтверждается. Для времени пребывания заявки в очереди в системе массового обслуживания не безразлично, какая дисциплина выборки заявок из очереди применена.
В заключение отметим, что рассмотренную проблему можно решать и методом однофакторного анализа. Однако если  (при сравнении двух выборок) целесообразно использовать изложенный метод.
(при сравнении двух выборок) целесообразно использовать изложенный метод.

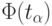 -
-