Рекурсивные алгоритмы и функции
Задание 3
- В программе укажите рекурсивные функции. Объясните работу рекурсивных функций.
- Проверьте работу программы при смене порядка объявлений функций.
- Проверьте работу программы без использования прототипов функций.
- Для случая, когда
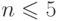 , предусмотрите вывод результата в строку, а не в столбец.
, предусмотрите вывод результата в строку, а не в столбец. - В программу добавьте программный код для подсчета рекурсивных вызовов, каждой из рекурсивных функций.
- остройте зависимость числа комбинаций заполнения и освобождения клеток от введенного числа n.
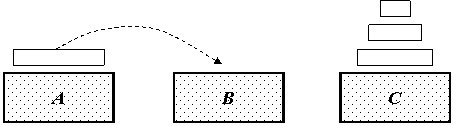
Пример 4. "Ханойская башня". Напишите программу по решению следующей задачи. Имеется пирамида из n колец, лежащих на основании А (на стержне, на столбе) одно на другом в порядке убывания размеров. Кольца должны быть перемещены на основание В в том же порядке, в котором они были на основании А, при использовании "промежуточного" основания С. Единственными разрешенными перемещениями являются такие, при которых кольцо, взятое с вершины одной из пирамид, помещается на большее кольцо, либо на пустое основание. Осуществить выдачу на печать (на консоль, в текстовый файл) последовательности перемещений колец.
"Ханойская башня" – известная задача. Алгоритм решения этой задачи достаточно подробно описан в [18.10].
Решение задачи "Ханойская башня"
Для рекурсивного решения этой задачи следует пройти три этапа.
1-й этап – параметризация. В этой задаче естественным параметром является n – число колец. В число параметров можно включить также и три основания: А (исходное), В (конечное), С (промежуточное).
2-й этап – поиск тривиальных случаев. Здесь тривиальным случаем будет такой, при котором n = 0; в этом случае просто нечего делать.
3-й этап – редукция общего случая к более простому. Здесь надо отметить, что n колец могут быть перемещены с А на В следующим путем:
- переноса (рекурсивно) n – 1 колец с вершины А (исходное основание) на С ("промежуточное" основание) с учетом правил: основание В (конечная цель) используется как промежуточное основание;
- перемещения на В кольца (наибольшего диаметра), оставшегося на А;
- переноса (рекурсивно) n – 1 других колец с С на В при соблюдении правил с А в качестве промежуточного основания.
Алгоритм решения задачи запишем в следующем виде:
hanoi(n–1, A, C, B); переместить (A, B); hanoi(n–1, C, B, A);
где hanoi() – имя рекурсивной функции [18.10].
Пример промежуточного положения Ханойской башни при n = 4 показан на рис. 18.4.
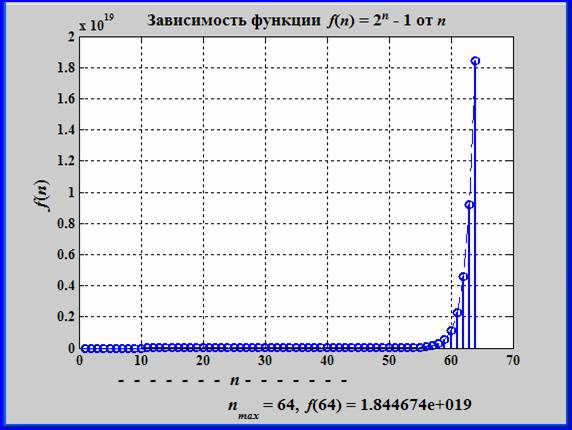
Число элементарных перемещений равно 2n – 1, где n – количество исходных дисков [18.10]. С увеличением n число перемещений быстро нарастает.
На рис. 18.5 показана зависимость элементарных перемещений от числа дисков.
С учетом того, что перемещение диска – это есть рекурсивный вызов функции, то на каждый вызов требуется определенное время. Практически с любым конечным малым временем обработки рекурсивного вызова общее время работы рекурсивной функции для большого количества дисков n становится не выполнимым на существующих современных компьютерах. В соответствии с легендой конец света наступит при перемещении 64 дисков [18.10].
В связи со степенным ростом числа рекурсивных вызовов в программе ограничимся величиной n = 15.
Программный код решения примера:
#include <stdio.h>
#include <conio.h>
#include <math.h>
// Пртотип рекурсивной функции
void hanoi(int n,char a, char b, char c);
int main(void)
{
char a = 'A'; // исходное основание
char b = 'B'; // конечное основание
char c = 'C'; // промежуточное основание
double n; // число дисков
char str[81] = "15"; // инициализация строки
puts("\n Hanoi Tower; A - starting; B - end; C - intermediate");
while (0.01) { // 0.01 - как истинное значение
printf("\n Enter the number of disks: ");
scanf_s(" %s",str, 80);
n = atof(str);
if ( n <= 0 || ceil(n) != n) {
printf("\n Error input. Press any key: ");
_getch();
continue;
}
else if (n > 15.0) {
printf("\n Very large number. Press any key: ");
_getch();
continue;
}
else
break;
}
puts("\n Elementary transferences:");
hanoi((int)n, a, b, c);
printf("\n\n Press any key: ");
_getch();
return 0;
}
// Определение рекурсивной функции
void hanoi(int num, char a, char b, char c)
{
if(num > 0) {
hanoi(num-1,a,c,b);
printf("\t%c --> %c\n",a,b);
hanoi(num-1,c,b,a);
}
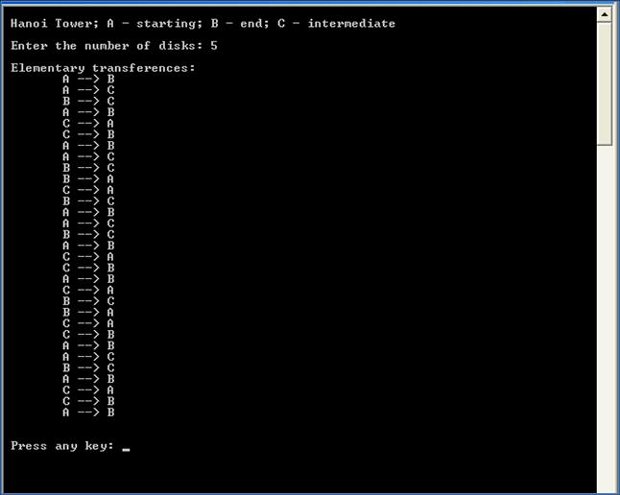
}Результат выполнения программы при n = 5 показан на рис. 18.6.
Задание 4
- Определите тип рекурсии, используемой в программе.
- Для случая, когда не все элементарные перемещения выводятся на экран дисплея, предусмотрите вывод результата программы в текстовый файл с именем compX.txt, где X – номер компьютера, на котором выполняется лабораторная работа.
- Программным путем выполните подсчет общего количества обращений к рекурсивной функции. Сделайте также вывод порядкового номера перемещения на экран дисплея. Порядковый номер расположите слева от элементарного перемещения. Построить (в MS Excel или в MATLAB) зависимость количества обращений к рекурсивной функции от заданного числа дисков.
- Измените аргументы рекурсивной функции: включить переменные типа int для определения имени (нумерации) основания.
- Измените условие задачи "Ханойская башня". Сначала исходным основанием считать В, конечным С, промежуточным А. Затем принять за исходное основание С, промежуточным В, конечным А.
Пример 5. "Задача о рюкзаке". Есть 10 предметов, о которых известны их веса и стоимости. Требуется поместить в рюкзак предметы таким образом, чтобы они не превысили допустимый вес для рюкзака при максимальной стоимости выбранных предметов. Исходные параметры модели – характеристики предметов взяты из [11] и приведены в табл. 18.1.
| Характеристики предметов | ||||||||||
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вес | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Стоимость | 18 | 20 | 17 | 19 | 25 | 21 | 27 | 23 | 25 | 24 |
Данная задача широко известна [18.9-18.10-18.11], она еще называется задачей о ранце, или вариант с английского – "knapsack problem". Предполагается, что один и тот же предмет не может быть взят несколько раз.
Для решения поставленной задачи используем рекурсивный алгоритм, описанный в [18.11], где также приводится фрагмент программы на языке программирования MODULA – 2.
Программный код решения примера:
#include <stdio.h>
#include <conio.h>
#include <locale.h>
const int limW = 20; // предельный вес выбранных предметов
enum {N = 10}; // количество предметов
typedef struct {
int weight; //// вес или размер предметов
int value; //// стоимость или ценность предметов
} object;
// Формирование структурного типа с параметрами модели
object obj[] = {10,18, 11,20, 12,17, 13,19, 14,25, 15,21, 16,27, 17,23, 18,25, 19,24};
int maxv; // для инициализации стоимости предметов
// Рекурсивная функция
int TRY (int i, int tw, int av) {
// Попытка включения предмета
if (tw + obj[i].weight <= limW)
if (i < N-1)
TRY(i+1, tw + obj[i].weight, av );
else if (av > maxv)
maxv = av;
// Попытка исключения предмета
if (av > maxv + obj[i].value)
if (i < N-1)
TRY(i+1, tw, av - obj[i].value);
else
maxv = av - obj[i].value;
return maxv;
}
// Главная функция программы
int main (void) {
int i, price;
int sumw = 0;
int sumv = 0;
setlocale(LC_ALL, "rus");
maxv = obj[0].value; // инициализации стоимости предметов
puts("\n\t\t\tЗАДАЧА О РЮКЗАКЕ");
puts("\t\t Характеристика предметов");
for (i = 0; i < (4*N + 12); i++)
printf("%s", "_");
printf("\n\n %12s", "Вес:");
for (i = 0; i < N; i++) {
sumw += obj[i].weight;
printf(" %3d", obj[i].weight); }
printf("\n %12s", "Стоимость:");
for (i = 0; i < N; i++) {
sumv += obj[i].value;
printf(" %3d", obj[i].value); }
printf("\n ");
for (i = 0; i < (4*N + 12); i++)
printf("%s", "_");
printf("\n\n %32s: %d\n", "Общий вес всех предметов", sumw);
printf(" %32s: %d\n", "Общая стоимость всех предметов", sumv);
printf(" %32s: %d\n ", "Допустимый вес рюкзака", limW);
for (i = 0; i < (4*N + 12); i++)
printf("%s", "_");
// Вызов рекурсивной функции с начальными параметрами
price = TRY(0,0,sumv);
printf("\n\n Стоимость выбранных предметов: %d\n ", price );
for (i = 0; i < (4*N + 12); i++)
printf("%s", "_");
printf("\n\n ... Нажмите любую клавишу: ");
_getch();
return 0;
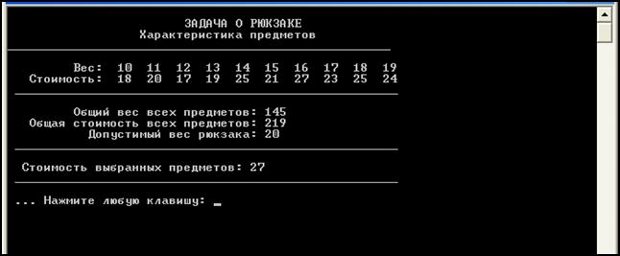
}Пример выполнения программы показан на рис. 18.7.
Представленная программа основана на следующем алгоритме [18.11]. В рекурсивной функции TRY() определены две ситуации для выбора предмета в рюкзак. Если речь идет о включении то объект (предмет со своим весом и стоимостью) можно включить в выборку для укладки в рюкзак, если он подходит по весовым ограничениям. Если он не подходит, то попытки добавить еще один объект в текущую выборку можно прекратить. Когда же речь идет об исключении, то критерием приемлемости, т. е. возможности продолжения построения текущей выборки, будет то, что после данного исключения общая ценность (стоимость) будет не меньше полученного до этого момента оптимума. В данной программе реализована схема с возвратами, использующая некоторые ограничения для уменьшения роста потенциального дерева поиска, называется алгоритмом ветвей и границ [18.11].