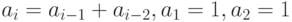Контрольная работа № 1

Вычисление последовательности Фибоначчи с использованием больших чисел

В языке программирования C существует большое количество разнообразных целочисленных типов данных, области определения которых охватывают числа различных диапазонов. При решении задачи программист должен выбрать правильные типы данных для числовых переменных, исходя из природы соответствующих данных, а также требований к занимаемой программой и ее данными памятью и желаемым быстродействием. Тем не менее, диапазоны встроенных целочисленных типов данных языка C ограничены, что не позволяет выполнять вычисления над достаточно большими числами (например, с разрядностью более 20 десятичных цифр). Такое ограничение оказывается серьезным препятствием при решении задач, природа которых требует выполнения операций над большими числами, например задач, требующих вычисления элементов быстрорастущих последовательностей. В частности, использование типа int языка C для вычисления элементов последовательности Фибоначчи позволяет получить только 46 первых чисел, после чего происходит целочисленное переполнение, и получение следующих элементов становится невозможным.

Такая проблема ограниченности диапазонов целочисленных типов данных решается при помощи так называемой "длинной арифметики". Длинная арифметика – в вычислительной технике операции над числами, разрядность которых превышает длину машинного слова данной вычислительной машины.

На практике длинная арифметика применяется в следующих случаях:

• На компьютеры с процессорами низкой разрядности и микроконтроллерах. Например, на компьютерах и микроконтроллерах с 8-битными процессорами без использования длинной арифметики невозможно выполнить никакие сколько-нибудь полезные вычисления;
• При решении задач криптографии;
• При создании математического и финансового программного обеспечения, требования к точности вычислений в котором очень высоки и критичны, а ошибки округления и переполнения недопустимы;
• Для "спортивных" вычислений знаменитых трансцендентных чисел ( , e и т. д.) с высокой точностью;
• Для решения олимпиадных задач по программированию.

Рассмотрим, каким образом можно хранить длинные целые числа в памяти компьютера и как выполнять над ними действия. Обычно длинное число представляют в виде массива, элементы которого хранят цифры длинного числа, и отдельно дополнительно сохранят длину числа, то есть количество значимых цифр. При хранении длинного числа удобнее перейти от десятичной системы счисления к системе счисления с большим основанием, так как это позволит лучше использовать пространство оперативной памяти, используемой под массив. Количество значимых цифр будем хранить в первом элементе массива (элементе с индексом 0). Цифры числа будем хранить в обратном порядке, то есть младшая цифра будет храниться в элементе массива с меньшим индексом.

Сделаем следующие объявления:

/// максимальная длина числа - 1000 знаков
#define NUMMAX		1000
/// основание системы счисления длинных чисел - 10^9
#define NUMBASE		1000000000
/// получениедлины числа
#define NUMLEN(n)	((n)[0])
/// определение типа длинных чисел
typedef int number_t[NUMMAX + 1];

Итак, мы определили тип данных длинных чисел – number_t. С его помощью можно хранить и обрабатывать числа длиной до 9000 десятичных знаков. Основание системы счисления выбрано равным 10⁹, это позволяет хранить в одном элементе массива до 9 десятичных знаков. Рассмотрим пример хранения двух чисел: 1 и 1234567890.

Число 1 меньше выбранного основания системы счисления, поэтому оно будет представлено одной значимой цифрой и для его хранения будет достаточно 1 элемента массива. Схема вышеприведенного описания может быть следующей:

Число 1234567890 больше выбранного основания системы счисления, поэтому оно будет представлено двумя значимыми цифрами и для его хранения потребуется 2 элемента массива. Схема приведенного описания может быть следующей:

Создадим три вспомогательные функции, выполняющие установку значения длинного числа. Функция numzero() устанавливает длинное число равным нулю. Программный код функции:

/// сброс длинного числа в ноль
void numzero (number_t lhs)
{
	lhs[0] = 1;
	lhs[1] = 0;
}

Функция numassgns() присваивает длинному числу короткое значение из диапазона 0..2³²–1. Программный код функции:

/// присваивание короткого числа длинному числу
void numassgns (number_t lhs, unsigned rhs)
{
	lhs[0] = 0;
	while (rhs)
	{
		lhs[++lhs[0]] = rhs % NUMBASE;
		rhs /= NUMBASE;
	}
}

Функция numassgn() присваивает одному длинному числу значение другого длинного числа. Программный код функции:

/// присваивание длинных чисел
void numassgn (number_t lhs, const number_t rhs)
{
	int i;

	// переписываем длину результирующего числа
	lhs[0] = rhs[0];
	// копируем цифры
	for (i = 1; i <= NUMLEN (rhs); ++i)
		lhs[i] = rhs[i];
}

Для вывода длинного числа на экран создадим функцию numprint(). Эта функция сначала проверяет длину числа, и если она равна 0, то выводит число 0, в противном случае она печатает цифры числа на экране проходя по массиву в обратном направлении, от индексов с большими значениями до индексов с меньшими значениями, так как цифры числа хранятся в обратном порядке. Программный код функции:

/// печать длинного числа
void numprint (const number_t lhs)
{
	int i;
    
	printf ("%d", NUMLEN (lhs) ? lhs[NUMLEN (lhs)] : 0);
	for (i = NUMLEN(lhs) - 1; i > 0; --i)
		printf ("%09d", lhs[i]);

}

Операция сложения длинных чисел реализует обычное сложение чисел столбиком. Вспомним, как выполняется такая операция. Пусть надо сложить два числа 12345 и 678. Записываем эти два числа в столбик таким образом, чтобы младшие разряды числа оказались друг под другом. После этого по таблице сложения складываем независимо разряды друг с другом. Если результат превосходит 9, то запоминаем 1, переносим ее в старший разряд, а в текущем разряде записываем младший разряд от результата сложения. И так продолжается до тех пор, пока все разряды не будут учтены. Обратите внимание, что если длина чисел разная, то в старших разрядах более длинного числа сложение производится только с "запомненной" 1 переноса. Схема вычислений может быть следующей:

Сложение чисел выполняется функцией numadd(). Функция принимает два числа – слагаемых и записывает результат в параметр с именем res. Функция выбирает из двух слагаемых более короткое и сначала складывает разряды двух чисел, затем, когда все разряды более короткого числа будут учтены, добавляет оставшиеся разряды более длинного числа с учетом переноса, признак которого хранится в переменной c. Так как цифры числа хранятся в обратном порядке, то сложение осуществляется в порядке возрастания индексов массива. Программный код функции:

/// сложение длинных чисел
void numadd (number_t res, const number_t lhs, const number_t rhs)
{
	int i = 0;
	// флаг переноса
	int c = 0;
	// число с минимальной длинной
	const int *sn = NUMLEN (lhs) < NUMLEN (rhs) ? lhs : rhs;
	// число с максимальной длиной
	const int *ln = sn == lhs ? rhs : lhs;
	
	// складываем два числа
	while (i < NUMLEN (sn))
	{
		++i;
		res[i] = c + sn[i] + ln[i];
		c = res[i] > NUMBASE ? 1 : 0;
		if (c) res[i] -= NUMBASE;
	}
	// добавляем остаток от более длинного числа и перенос
	while (i < NUMLEN (ln))
	{
		++i;
		res[i] = c + ln[i];
		c = res[i] > NUMBASE ? 1 : 0;
		if (c) res[i] -= NUMBASE;
	}
	// учитываем последний перенос
	if (c) res[++i] = c;
	// сохраняем длину числа
	res[0] = i;
}

Рассмотрим пример использования арифметики длинных чисел. Функция main() создает три переменные для хранения длинных чисел, инициализирует из значениями, и выполняет операцию сложения, после чего печатает результат на экране. Программный код главной функции:

int main (int argc, char* argv[])
{
	int i;

	number_t a, b, c;
	numassgns (a, 1234567890);
	numassgns (b, 1);
	numadd (c, a, b);
	numprint (c);

     printf("\n\n ... Press any key: ");
    _getch();

	return 0;
}

Задание:

1. Создайте функцию numtoa (), выполняющую преобразование длинного числа в строку. Функция должна иметь следующий прототип:

   /// перевод длинного числа в строку
   void numtoa (const number_t num, char *str);
2. Создайте функцию atonum (), выполняющую преобразование строки в длинное число. Функция должна иметь следующий прототип:

   /// перевод строки в длинное число
   void atonum (const char *str, number_t num);
3. Разработайте программу, выполняющую вычисление 500 первых чисел последовательности Фибоначчи. Элементы последовательности Фибоначчи вычисляются по следующему рекуррентному соотношению: