|
"Тогда как задать возбуждение рецепторов, если инспектор точно установил, что скорость автомобиля при наезде на пешехода была равна 114 км/час? Вопрос по расчёту скорости и сумме достоверности: этот математический (приведенный выше в виде контекста из материала лекции 1, страницы 3) метод справедлив к скоростным показателям выходящим за рамки диапазона 100-120. |
Методика построения системы принятия решений на основе логической нейронной сети
Общие рекомендации
Поразмыслив аккуратно,
Я избрал себе дорожку
И иду себе без шума,
Понемножку, понемножку!
Объединим ряд рекомендаций, рассредоточенных выше.
1. Можно понять Природу, где сначала создаётся необученный мозг, который всю жизнь следует заполнять знаниями. Другое дело наши разработки средств хранения и ассоциативной выборки знаний.
Зачем нам идти таким кружным путём: сначала выбирать нейросеть, а затем заполнять её знаниями – обучать? Разве только для достижения максимального наукоподобия наших исследований?
Занимаясь конкретной задачей распознавания, управления или принятия решений, мы стремимся к максимальному упрощению решения этой задачи искусственного интеллекта. Ведь мы можем сразу построить уже обученную нейронную сеть на основе логического описания задачи! Мы видели, что такая нейросеть допускает любое развитие.
С досадой воспринимается случай, когда исследователь, даже прослушавший курс, не признаёт предлагаемых результатов. Он следует "классическим" путём, упоминаемым выше, и с удивлением выслушивает замечание:
- Смотри, ты в результате обучения методом "обратного распространения ошибки" получил те самые синапсические веса, которые ты мог получить при непосредственном построении обученной логической нейронной сети на основе логического описания твоей системы принятия решений! Но это – слишком просто?!.
2. Мы видим, что в природе нейрон - инструмент выполнения функции активации. Работа "живого" нейрона, обусловленная "мясными" технологиями, сложна. Известно, что для его возбуждения должны свершиться до 240 химических реакций! Но нас интересует только логика его работы, и моделировать эти реакции на логическом уровне нет смысла. Информационные технологии логических нейронных сетей используют простые функции активации, некоторые виды которых рассмотрены выше. Однако при моделировании нейрон может воспроизводиться как аппаратно – в составе нейрокомпьютера, так и в виде программной процедуры. Так, в общем, и следует считать: нейрон (нейроподобный элемент) – это инструмент реализации процедуры выполнения функции активации.
3. Корректно построенная система принятия решений при формировании факторного пространства учитывает использование исчерпывающих множеств событий . Например, это означает, что если используются времена года, то должны учитываться все эти времена. Иначе СПР будет не полной. Отрицание некоторой переменной - события, встречающееся в описании СПР, подразумевает, что имеет место некоторое другое событие из того же исчерпывающего множества. Например, операция отрицания НЕ "зима" означает, что "или весна", "или лето", "или осень". Записывается: НЕ "зима" = "весна" ИЛИ "лето" ИЛИ "осень".
Это означает, что в логическом описании СПР в общем случае логическая операция отрицания не участвует, а участвуют только операции конъюнкции и дизъюнкции.
Более того, составив логическое описание, не следует торопиться с его воплощением в виде логической нейронной сети. Описание может быть преобразовано так, чтобы нейросеть получилась наиболее простой и обеспечивала максимальную достоверность выводов.
Тогда, можно представить технологию построения логической нейронной сети для системы принятия решений.
- Строится граф-схема логического описания СПР, содержащая рецепторы для ввода переменных, конъюнкторы, дизъюнкторы и связи между ними. (Такая схема эквивалентна электронной схеме устройства, выполняющего роль СПР.)
- Обозначение конъюнкторов и дизъюнкторов заменяется обозначением нейрона (нейроподобного элемента).
- Выбирается подходящая функция активации из числа известных, простых, рекомендуемых или предлагаемых автором - разработчиком.
Нейронная сеть готова к употреблению по нечётким данным! Необходимо лишь произвести её верификацию по известным решениям.
Ещё раз отметим (это – настоятельная рекомендация!), что всегда существует возможность так упростить логическую нейронную сеть, что она сделается однослойной. Однослойная сеть, помимо слоя рецепторов, обладает единственным слоем нейронов – носителей функции активации (если отсутствуют обратные связи). Этот слой является и выходным.
Построение однослойной нейронной сети производится на основе представления всех логических функций, образующих описание СПР, в дизъюнктивной нормальной форме . Далее, если необходимо, производится размножение решений – закрепление одинаковых решений за одной или несколькими конъюнкциями (объединёнными дизъюнкцией) отдельно. (Отметим, что при построении однослойной сети для дяди Рамзая мы не строили дизъюнкцию конъюнкций, но нейронная сеть работает правильно!) Важно отметить, что размноженные решения не долго остаются одинаковыми. Ведь целесообразно дополнить текст этих решений хотя бы указанием на то, по какой причине они принимаются.
А как строить логические нейронные сети с обратными связями? Не являются ли рекомендации выше ориентированными исключительно на формальный подход? Да, несомненно, доля формализма здесь присутствует, и при введении обратных связей не обойтись без творческого осмысления сути предмета исследования – того реального процесса управления, который предстоит автоматизировать.
Практическая рекомендация здесь может заключаться в следующем:
По указанной методике следует построить логическую нейронную сеть без обратных связей. Затем, применив известную долю изобретательности, добавить в нейросеть обратные связи, как это было продемонстрировано в "Развитие логической нейронной сети для распознавания объектов по заданному набору признаков" , "Логические нейронные сети с обратными связями" и "Нейросетевые модели пошаговой оптимизации, маршрутизации и тактических игр" . Примеры показывают, что веса обратных связей могут быть как положительными, так и отрицательными, а также – переменными. Вместе с тем и выбор функции активации может представлять творческую, остроумную задачу.
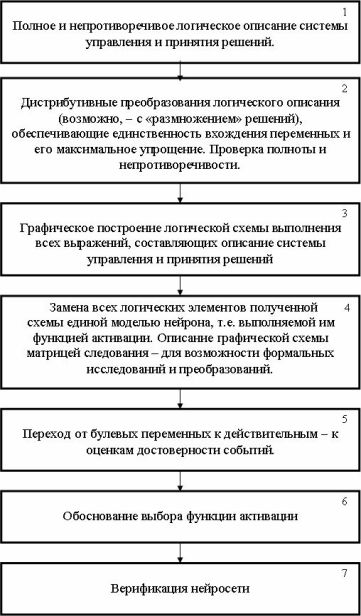
Основные этапы работ
На рис.13.1 представлены основные этапы построения СПР.
Логическое описание системы принятия решений
Ассоциативному мышлению адекватны логические нейронные сети, создаваемые на основе логического описания системы управления или принятия решений в терминах алгебры высказываний о принадлежности исходных данных – значениям, объектам, диапазонам изменений. Если СПР функционально полностью определена и может быть описана в терминах математической логики, то по этому описанию целесообразно строить уже обученную нейронную сеть. Несложность такого построения способствует тому, что при модификации СПР обученная нейросеть может легко развиваться либо быть построена заново. В то же время правомерен подход, при котором нейросеть заданной структуры обучается для конкретного применения или переобучается. Алгоритмы такого обучения представлены в [6, 7].
Структура обученной логической нейросети полностью совпадает со структурой логической схемы системы управления и принятия решений.
Составление полного и непротиворечивого логического описания – первый этап выполнения методики построения логической нейронной сети для СПР.
Ранее показывалось, что в терминах алгебры высказываний (математической логики) СПР описывается системой логических выражений вида

 |
( 13.1) |

где  , — логические переменные-высказывания о наступлении событий, принимающие значения ИСТИНА (1), если событие наступило, и ЛОЖЬ (0) в противном случае;
, — логические переменные-высказывания о наступлении событий, принимающие значения ИСТИНА (1), если событие наступило, и ЛОЖЬ (0) в противном случае; 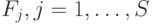 , — логические функции указанных переменных-высказываний, значение ИСТИНА которых определяет принимаемое решение
, — логические функции указанных переменных-высказываний, значение ИСТИНА которых определяет принимаемое решение 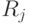 .
.
Для непротиворечивости и полноты СПР необходимо и достаточно, чтобы для каждого набора высказываний не более чем одна логическая функция в (13.1) принимала значение ИСТИНА и чтобы не существовало такого набора переменных-высказываний на основе факторного пространства событий, для которого в системе (13.1) все логические функции имеют значение ЛОЖЬ.
Напоминаем, что при логическом описании СПР используются операции конъюнкции и дизъюнкции, но не используется операция отрицания. Это объясняется тем, что в интересах корректности и полноты отображения предмета исследований в СПР каждый задействованный фактор должен учитываться в рамках модели исчерпывающего множества событий . Учитываются все возможные значения или состояния этого фактора. Каждый фактор А представлен множеством состояний (событий, значений, диапазонами значений) 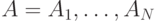 .
.
Это множество формируется так, что выполняется условие нормировки  , где
, где 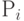 — предполагаемая пользователем (!) вероятность (достоверность) наступления события
— предполагаемая пользователем (!) вероятность (достоверность) наступления события  .
.
Например, при построении системы штрафования водителей за превышение скорости V представляется логичным охват всего возможного диапазона предполагаемого превышения, например:
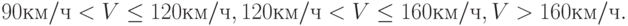
Такое описание учитываемого фактора, в данном случае – скорости, не оставляет открытым вопрос: "Что делать, если скорость принадлежит неучтённому диапазону изменения?"
При рассмотренном способе корректного и полного учёта всех возможных событий отрицание некоторого события означает возможность альтернативного выполнения (в смысле логической операции ИСКЛЮЧАЮЩЕЕ ИЛИ) всех других событий из исчерпывающего множества:
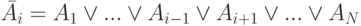
Дистрибутивные преобразования логического описания и возможности упрощения
Вторым этапом выполнения методики, в силу специфики дальнейшего перехода от булевых переменных к достоверности событий, является дистрибутивное преобразование логических функций (13.1) к виду, который обеспечивает единственность вхождения всех переменных, участвующих в одном логическом выражении. При этом рассмотрение лишь исчерпывающих множеств событий приводит к отсутствию их отрицаний.
Это преобразование во многом основано на свойстве дистрибутивности конъюнкции по отношению к дизъюнкции и дизъюнкции по отношению к конъюнкции.
Правила эквивалентных преобразований логических выражений широко известны. (В теории математической логики такое преобразование связано с формированием дизъюнктивной или совершенной дизъюнктивной нормальной формs .) Однако указанная специфика свойства дистрибутивности гарантирует возможность с помощью последовательного вынесения за скобки обеспечить единственность вхождения каждой используемой переменной в отдельное логическое выражение.
Необходимость такого преобразования обусловлена заменой операций конъюнкции и дизъюнкции их приближённым "суррогатом" — функцией активации. Практически такая функция основана на суммировании (взвешенных) сигналов на входе нейрона. Тогда неоднократность вхождения, т.е. суммирования, одних и тех же сигналов становится недопустимой.
Однако не всегда подобное преобразование приводит к успеху. Тогда используется приём размножения решений , основанный на том, что логическое выражение разбивается на составляющие выражения - конъюнкции, объединённые операцией дизъюнкции. (Это и есть дизъюнктивная нормальная форма .) Для всех таких выражений, заменяющих прежнее, определяется одинаковое решение.
В результате преобразований каждое выражение логического описания в общем случае представляет собой скобочную запись с более чем одним уровнями вложенности.
Однако указанное свойство функции активации, сводящей две логические операции к одной - арифметической, порождает возможность существенного упрощения нейросети, а именно, — сведение её к однослойной.
Ранее было показано, что с помощью приёма размножение решений такое сведение всегда возможно. Однако оно приводит к "дроблению" сети, к размножению путей получения одних и тех же решений, к перегрузке сети заданной фиксированной структуры на этапе её обучения.
В то же время многие реальные процессы по самому смыслу своему (экономические системы, управляющие, технологические и др.) адекватны не просто однослойным логическим нейронным сетям, но даже сетям совершенным. В их описании левая часть каждого логического выражения является конъюнкцией "представителей" обязательно всех исчерпывающих множеств событий , в совокупности образующих факторное пространство.
Анализ на возможность построения однослойной нейросети целесообразно проводить на этом же этапе выполнения методики до выполнения дистрибутивных преобразований.
Самый простой способ такого анализа заключается в следующем. Для каждого логического выражения в (13.1) выпишем без повторения множества используемых в них переменных (сформируем обобщённые эталоны). Проведём совместный анализ обобщённых эталонов, составленных по всем логическим выражениям, и установим, отсутствует ли полное вхождение одного из таких эталонов в другой? Если такое вхождение отсутствует (пересечение обобщённых эталонов допустимо), то возможно построение однослойной нейросети, т.е. непосредственное соединение связями нейронов-рецепторов с нейронами выходного слоя. Более того, если все обобщённые эталоны содержат одинаковое число переменных, возможно построение совершенной нейронной сети.
Если некоторый обобщённый эталон входит в состав другого, а разработка связана какими-то дополнительными условиями (структура сети задана, известная сеть доучивается и др.), необходимо полное воспроизведение структуры логических связей, что приводит к многослойной нейросети. Мы в этой книге не рассматриваем подробно возникающие при этом трудности [6], но должны предупредить, что при реализации структурированного логического описания возникают проблемы. Они связаны и с более сложным алгоритмом трассировки, и с необходимостью коррекции порогов, а также весов связей – для повышения достоверности результатов. (При построении нейронов – конъюнкторов и нейронов – дизъюнкторов в Лекциях 2 и 3 мы видели, что веса синапсических связей нейрона для реализации этих функций различны.)
Так что стремитесь построить однослойную, ещё лучше, - совершенную логическую нейронную сеть ! Это всегда возможно, если следовать по пути первоначального накопления базы знаний (БЗ) на основе нахождения связи между исследуемыми ситуациями и принимаемыми по ним правильными решениями. Тем более что такой подход на уровне логического описания приводит к применению только конъюнкций. Следовательно, все нейроны сети используются одинаково. Каждый реализует "суррогат" конъюнкции.