Методика построения системы принятия решений на основе логической нейронной сети

Построение логической схемы

На третьем этапе графически, в соответствии со схемотехническим подходом, применяемым в технологии построения электронных схем, составляется логическая схема выполнения всех выражений (13.1), преобразованная на втором этапе. Логические функции реализуются с помощью конъюнкторов и дизъюнкторов, связанных между собой в соответствии с представленными логическими функциями. При этом скобочная запись активно диктует структуру и взаимодействие логических элементов.

Такое представление соответствует общему виду (13.1). При допустимости построения однослойной нейросети, как говорилось выше, схема представляет собой структуру, при которой входы, на которые подаются переменные, непосредственно связаны с выходами, соответствующими решениям.

Переход к нейронам

Четвёртый этап позволяет ввести в рассмотрение неопределённость и заключается в замене конъюнкторов и дизъюнкторов единой моделью нейрона, реализующего одну из простейших функций активации. Такая замена позволяет перейти от задания булевых переменных на входе (есть событие – нет события) к вероятности (достоверности) высказываний о наступлении этих событий, то есть, к заданию предполагаемых действительных оценок событий.

За каждым событием оказывается закреплённым нейрон входного (рецепторного) слоя. Если событие отображает значение некоторого фактора, например, температуры, то весь диапазон значений этого фактора разбивается на достаточные по точности малые диапазоны. Тогда при запросе к нейросети (в рабочем режиме) событие оценивается достоверностью того, что значение фактора принадлежит некоторому (возможно, нескольким – с предполагаемой долей вероятности) диапазону.

Такое разбиение областей значений факторов производится на этапе логического описания СПР так, чтобы впоследствии, на данном этапе выполнения методики, за каждым диапазоном оказался закреплённым нейрон – рецептор. Тогда события задаются достоверностью принадлежности значений факторов одному или более диапазонам изменения.

Однако не обязательно за диапазонами изменения значений закрепляются рецепторы. Могут быть использованы опытные или экспериментальные значения (в этом случае изучаются не диапазоны принадлежности данных, а точки). Это скажется лишь при задании достоверности исходных данных на основе их "близости" значениям, для которых известны решения, как это рассматривалось, например, в лекции 11.

Напомним, что при корректной постановке задачи сумма значений возбуждения рецепторов, соответствующих одному фактору, должна быть равна единице. Более того, эти возбуждения (внутри одного фактора) должны имитировать нормальный закон распределения вероятностей. Однако это замечание относится уже к режиму эксплуатации.

В графическом исполнении нейросеть неудобна в работе. Матрица следования, эффективность которой для представления и обработки параллельных процессов доказана, позволяет строить простые алгоритмы и программы для выполнения всех операций над нейронами и связями нейросети.

В матрице следования за каждым нейроном закрепляется строка и столбец с номером нейрона. В строке указываются значения весов тех связей, которые исходят от некоторых нейронов и поступают в данный.

Выбор и обоснование функции активации нейрона

На пятом этапе производится обоснование выбора функции активации нейронов.

Функция активации должна лишь условно, с наименьшей трудоёмкостью воспроизводить аналог операций конъюнкции и дизъюнкции. Нет необходимости в моделировании реальных процессов, происходящих в нейроне. Более того, ведь нас интересует только логика мышления, а не физические и химические механизмы её реализации, сопровождающиеся сложными переходными процессами в отдельном нейроподобном элементе.

Требования к функции активации:

• эти функции в области преодоления порога должны быть монотонно возрастающими по каждому сигналу на входе нейрона;
• не должно быть "угасания" сигнала возбуждения при его прохождении по сети;
• сигналы возбуждения на выходном слое должны быть четко различимы по величине для различных эталонных ситуаций;
• должен быть примерно равным диапазон изменения величин возбуждения нейронов выходного слоя, закрепленных за разными решениями.

Приведём ряд функций активации, тривиальных по выполнению и используемых в данной книге:

1. 
   
2. 

   
3. 

   
4. 

   

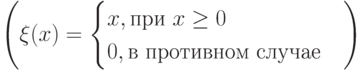
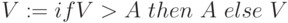
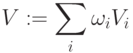
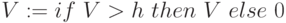
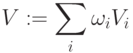
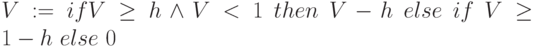
   Вес связи – переменная с двумя индексами; здесь не индексируется нейрон, а только его вход.

5. Достаточно универсальной функцией активации является функция возбуждения нейрона по усреднённому значению сигналов на его входах (дендритах). Это усреднённое значение сигналов и принимается, как величина возбуждения нейрона.

   
   

Если все веса , то функция активации находится:

Не следует забывать, что нейронную сеть, реализующую СПР, необходимо рассматривать как одно звено в цепочке логического вывода, вырабатывающее информацию для последующих звеньев цепочки. Это позволяет строить сложные, многоуровневые СПР, как цепочки логических выводов, реализующие дедуктивное и даже индуктивное мышление.

Конкретно это означает, что величины возбуждения нейронов выходного слоя должны, как и величины возбуждения рецепторов, принадлежать диапазону [0, 1], моделируя всё ту же достоверность выводов.

В однослойных нейронных сетях, особенно – в совершенных - предлагается использовать функцию активации 5. Здесь особенно актуально то, что прообразом нейрона выходного слоя является конъюнктор. Легко видеть, что величина возбуждения каждого нейрона сети удовлетворяет указанному диапазону.

Отметим, что в однослойных сетях хороша каждая из перечисленных функций активации.

Функция активации 4 применима в задачах логического вывода, а также в системах диагностики, т.к. близка к воспроизведению булевой переменной.

Можно придумать и другие функции активации, удовлетворяющие приведённым выше требованиям.

Однако в сложных структурированных логических сетях следует осторожно выбирать функцию активации. Различие длин динамических путей возбуждения, ведущих от разных рецепторов к одному выходу, требует выполнения свойства аддитивности. Иначе это может приводить либо к применению разных функций активации для имитации конъюнкторов и дизъюнкторов, либо к специальной корректировке весов и порогов.

По-видимому, два последних пункта комплексно определяют действия разработчиков при введении обратных связей, хотя, несомненно, эти связи учитываются уже при логическом описании системы принятия решений. Их нецелесообразно формально учитывать при дистрибутивных преобразованиях, сводящих нейросеть к однослойной.

Так, в "Нейросетевые модели пошаговой оптимизации, маршрутизации и тактических игр" (технология Wi-Fi), при "единичных" запросах на смещение информационного пакета в смежный узел по чёткому адресу, функция активации выродилась в сумму весов связей нейрона.